[c++] 백준 12015 가장 긴 증가하는 부분 수열 2 (최장 증가 부분 수열 / LIS / Longest Increasing Subsequence / 이분 탐색 / binary search / nlogn)

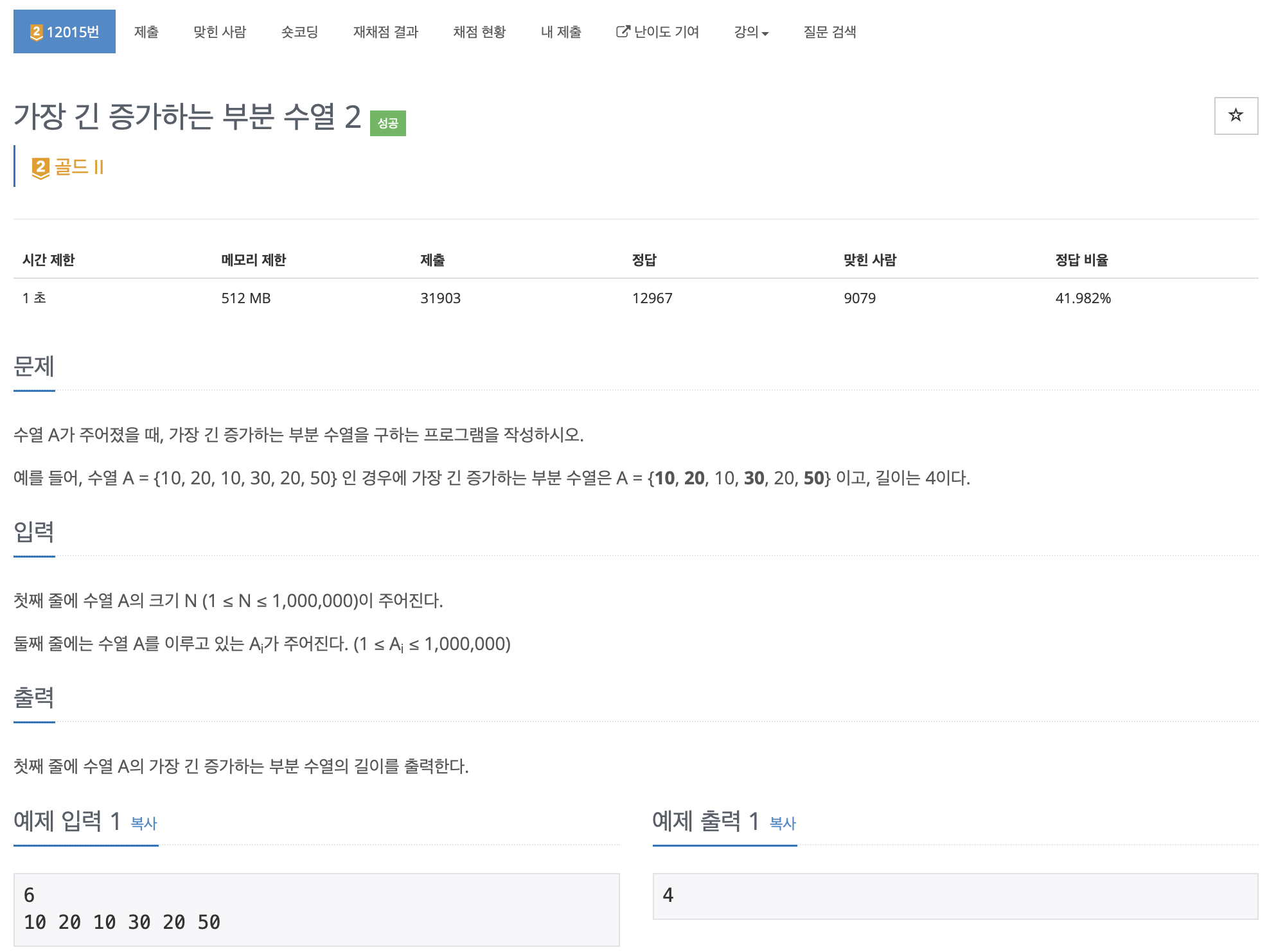
https://www.acmicpc.net/problem/12015

LIS (Longest Increasing Subsequence)

주어진 '수열' 에서 일부 원소를 뽑아내어 새로만든 수열이 '부분 수열'
이 수열이 '오름차순' 인 수열이 '증가하는 부분 수열' 이 된다.
만들 수 있는 오름차순 수열 중, '가장 긴' 수열이 LIS가 된다.

Before Solution

DP VS Binary Search

블로그를 기제하는 이유중 핵심은 "Binary Search". 즉, 이분탐색 때문이다.
LIS 유형은 DP로도 풀 수 있고, Binary Search로도 풀 수 있다.

이 전에 가장 증가하는 긴 부분 수열 문제(https://www.acmicpc.net/problem/11053)를 풀 때, DP로 풀었어서, 이 문제도 똑같이 풀었으나 "시간초과"가 난다.

이유는 DP로 풀면 O(N^2)이지만, 이분 탐색으로 풀면 O(NlogN)만큼 걸리기 때문

+)DP풀이는 상당히 간단함. dp배열 만들어서 이중for문 돌리면 됨

Solution

'a배열의 원소'와 'lis배열의 마지막 원소'를 비교 O(N)
-> 더 크다면 lis배열의 마지막에 추가.
-> 작다면 Binary Search를 이용하여 자리 탐색 O(logN)

그림으로 보면 훨씬 이해하기 편하다.

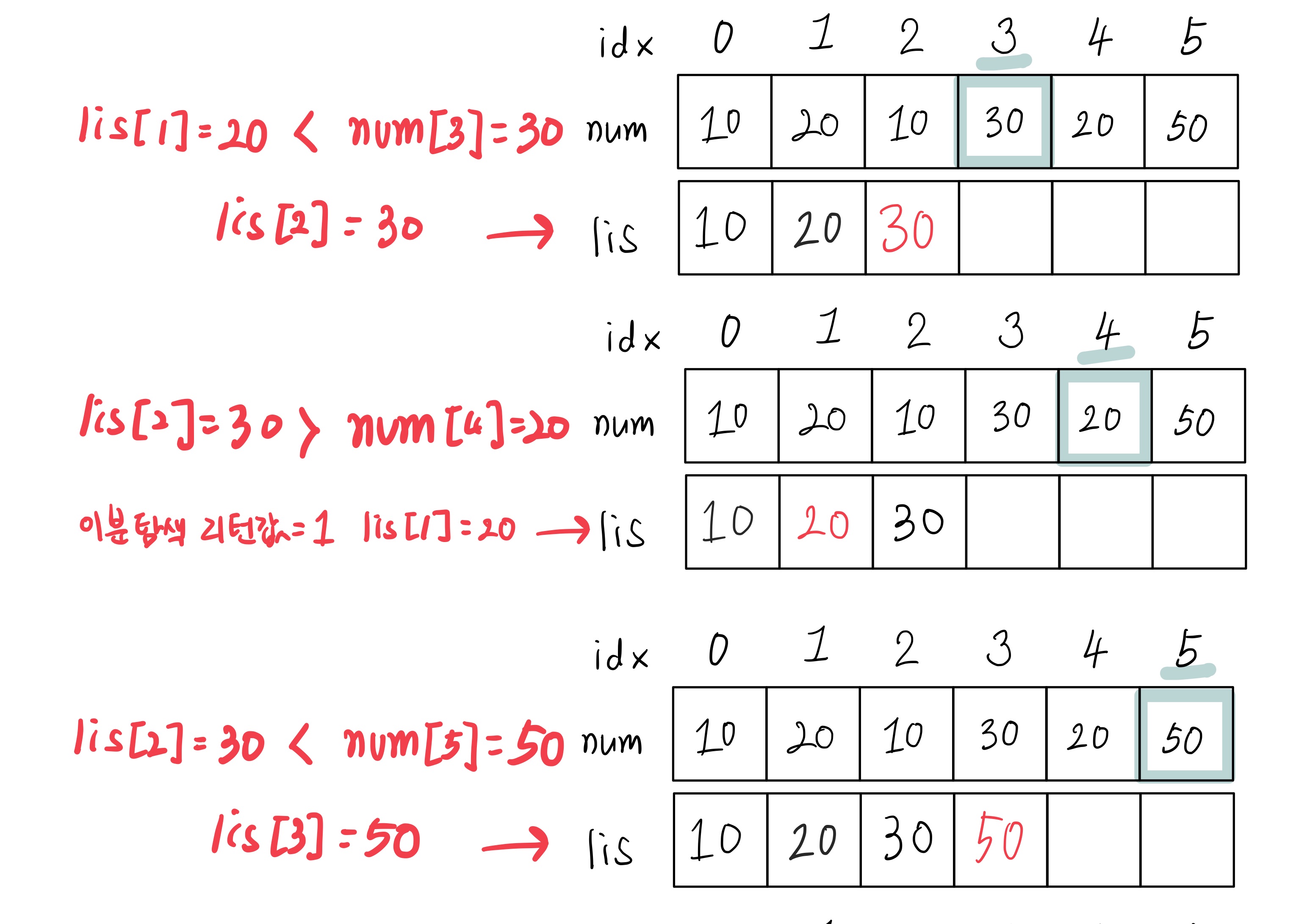
첨언하자면 큰 값이면 뒤에 추가하고, 큰 값 보다 작은 값이면 적절한 자리를 찾아서 넣어준다.
증가하는 부분수열 {1,3,9}와 {1,3,5}가 있을때, 두 수열의 길이는 3으로 동일하다. 하지만 "가장 긴" 증가하는 부분 수열을 만들려면, 가장 뒤 원소가 최솟값인게 유리 할 것이다.
그러니까 뒤에 원소가 7일때 {1,3,9} 뒤에는 7을 못 붙이는데 {1,3,5}뒤에는 7을 붙일 수 있다는 뜻.
이해가 안 간다면 직접 손으로 계산해보길 바란다.

int j = 0;
    lis[0] = a[0];
    for (int i=0; i<n; i++){
        if (lis[j] < a[i]){
            lis[j+1] = a[i];
            j++;
        }
        else{
            int idx = binarysearch(0, j, a[i]);
            lis[idx] = a[i];
        }
    }

Binary Search

정렬되어 있는 배열 left ~ right 사이의 중간위치 mid를 구하여 array[mid]의 값과 타겟을 비교한다.
-> 타겟이 mid의 값보다 작다면 : right = mid
-> 타겟이 mid의 값보다 크다면 : left = mid + 1;
시간복잡도가 O(logN)

lis배열은 정렬되어있는 배열이기때문에 이분탐색으로 적절한 위치를 찾을 수 있다.
이분 탐색에 대해 이해가 안간다면 따로 알아보자.

int binarysearch(int left, int right, int target){
    int mid;
    while (left < right){
        mid = (left + right)/2;
        
        if (lis[mid] < target)
            left = mid + 1;
        else
            right = mid;
    }
    
    return right;
}

이게 끝이다.
생각보다 간단함!

전체코드

#include <iostream>
#include <algorithm>
using namespace std;

int n,a[1000005]={0,},lis[1000005]={0,};

int binarysearch(int left, int right, int target){
    int mid;
    while (left < right){
        mid = (left + right)/2;
        
        if (lis[mid] < target)
            left = mid + 1;
        else
            right = mid;
    }
    
    return right;
}

int main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);

    cin>>n;
    for(int i=0; i<n; i++)
        cin>>a[i];
    
    int j = 0;
    lis[0] = a[0];
    for (int i=0; i<n; i++){
        if (lis[j] < a[i]){
            lis[j+1] = a[i];
            j++;
        }
        else{
            int idx = binarysearch(0, j, a[i]);
            lis[idx] = a[i];
        }
    }
    
    cout<<j+1;
        
    return 0;
}

dp로 풀면 시간초과납니다.