[c++] 백준 11758 CCW (CCW / Counter Clockwise)

https://www.acmicpc.net/problem/11758

CCW / Counter Clockwise

CCW란?

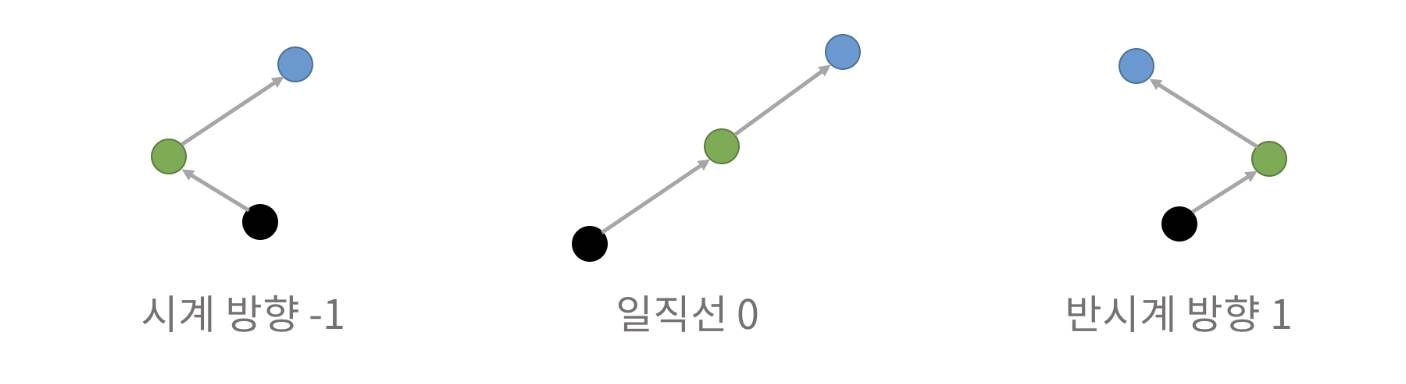
평면 위에 놓여진 세 점의 방향관계를 구할 수 있는 알고리즘
점 a,b,c를 순서대로 검사하여 반시계방향으로 놓여있으면 양수를, 시계방향이면 음수를, 평행하면 0을 리턴한다.

기하 알고리즘의 한 종류입니다.

벡터의 외적

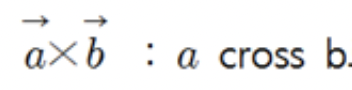외적의 결과로 외적에 쓰인 두 벡터와 동시에 수직인 벡터를 구할 수 있다. 이 수직벡터의 방향으로 세 점의 방향을 판단 할 것이다. +) 외적은 교환법칙 성립 X (크기는 같음) +) 단위벡터 : 길이가 1인 벡터 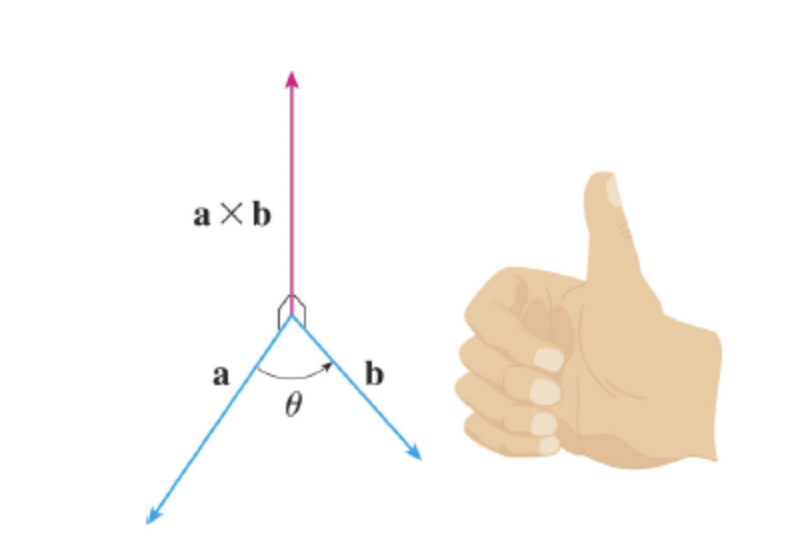방향은 오른손 법칙을 따른다.

좀 더 부가적인 설명을 해보자면, 두 벡터의 결과를 행렬식으로 나타내어보자.

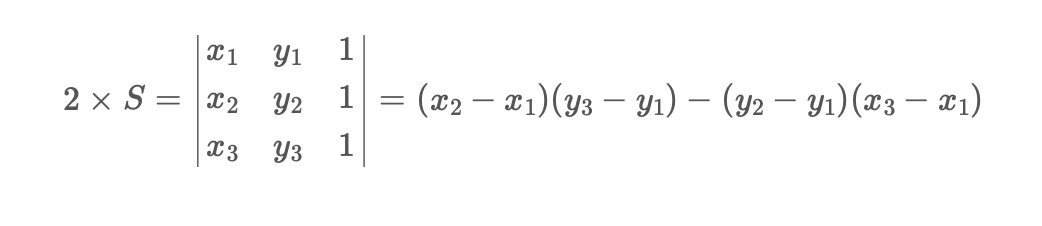
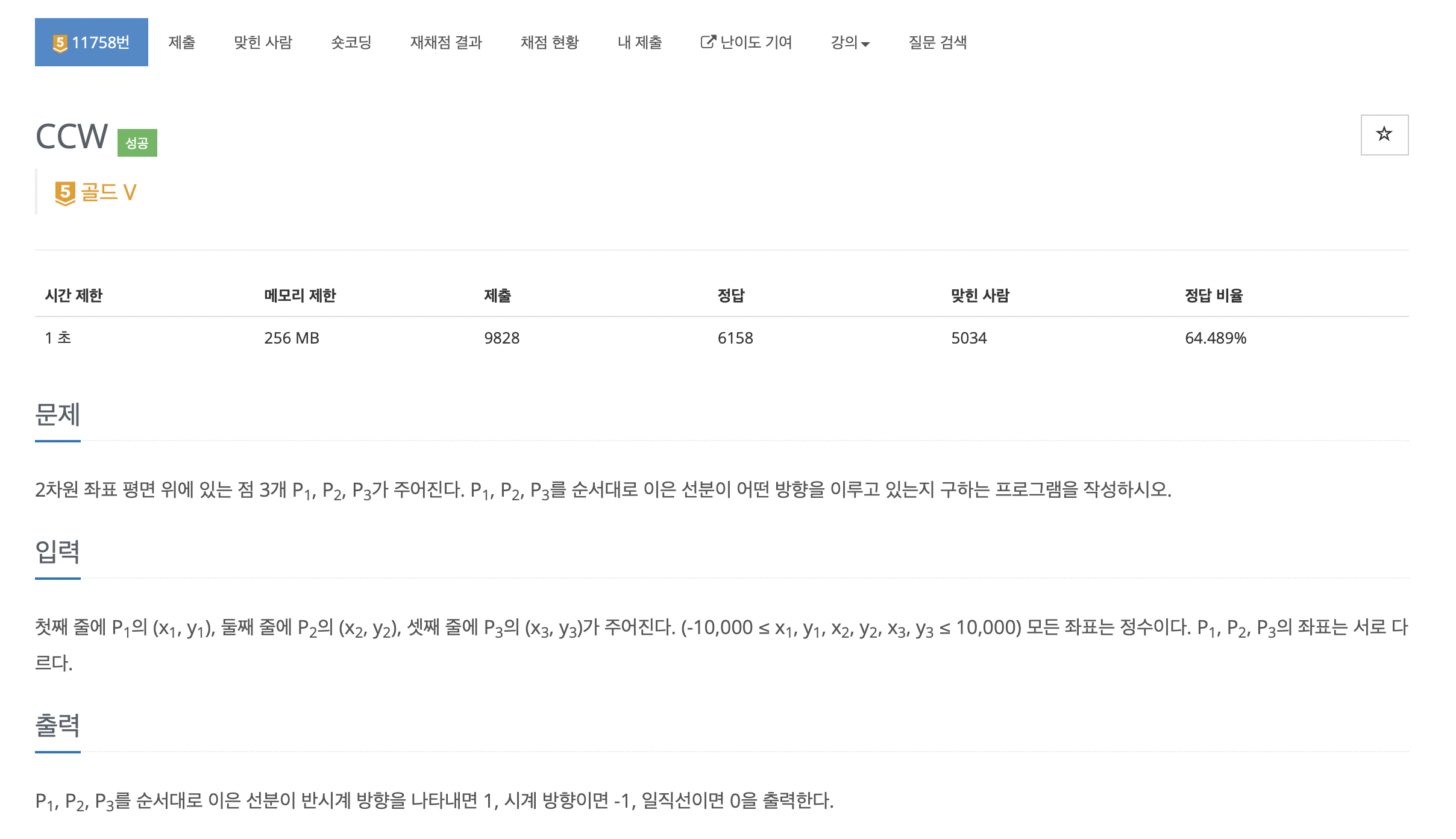
여기서 S의 부호에 따라서 세가지로 나눈다.

• s > 0 : 반시계방향
• s = 0 : 일직선
• s < 0 : 시계방향

구조체 구현

struct pos {
    int x,y;
};

간단하게 x,y좌표로 나타내었다. 매번 pair만 썼는데 구조체 깔끔하고 좋은 듯.

핵심 코드

long long tmep = (b.x - a.x)*(c.y - a.y) - (c.x - a.x)*(b.y - a.y);

행렬식을 그대로 이용하여 코드를 짰다. 깔끔하다.

내 코드

long long temp = a.x * b.y + b.x * c.y + c.x * a.y - (b.x * a.y + c.x * b.y + a.x * c.y);

나는 저 방법을 알기전에 신발끈 공식을 이용하여 코드를 짰다. 다만 코드가 길어지니 나도 다음부터는 위 코드를 이용할 생각이다.

전체코드

#include <iostream>
using namespace std;

struct pos {
    int x,y;
};

int main(int argc, const char * argv[]) {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    
    pos a,b,c;
    cin>>a.x>>a.y;
    cin>>b.x>>b.y;
    cin>>c.x>>c.y;
    
    long long temp = a.x * b.y + b.x * c.y + c.x * a.y - (b.x * a.y + c.x * b.y + a.x * c.y);
    
    if (temp < 0)
        cout<<"-1";
    else if (temp > 0)
        cout<<"1";
    else
        cout<<"0";
    
    return 0;
}