1. 언어 모델

---

1.1. 언어 모델과 확률적 접근

언어 모델(Language Model)이란 주어진 텍스트의 맥락을 바탕으로 다음에 올 단어나 문장을 예측하는 알고리즘을 의미한다. 즉, 단어 시퀀스 $(w_1, w_2, \dots, w_n)$에 대한 확률 $P(w_1, w_2, \dots, w_n)$을 추정하는 모델을 뜻한다. 예컨대 이 확률값이 높을수록 해당 단어들의 나열(문장 혹은 구문)이 자연스럽거나 흔히 사용된다고 볼 수 있다.

자연어 처리(NLP)에서 언어 모델은 문장 완성, 기계 번역, 음성 인식, 질의응답 등 광범위한 과제에서 중요한 역할을 한다. 특히 텍스트 자동생성이나 자동완성 기능을 구현할 때, 언어 모델은 뒤이어 나올 단어나 토큰을 가장 높은 확률을 가진 형태로 제시함으로써 높은 유용성을 제공한다.

전통적 언어모델부터 현재 이르기에는 GPT, BERT 등의 더욱 진보된 언어모델이 존재하지만, 여기서는 전통적 언어모델인 n-gram language model에 대해서 살펴보기로 하자.

1.2. n-gram

1.2.1. n-gram이란?

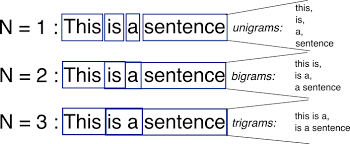
• n-gram은 연속된 $n$개의 단어(또는 문자)로 구성된 그룹을 의미한다.
• 여기서 $n$은 그룹을 구성하는 단어(또는 문자)의 개수를 나타낸다.
• 텍스트에서 연속된 단어(또는 문자)를 조합하여 언어 모델을 구성하는 데 사용된다.

1.2.2. n-gram의 종류

$n$의 크기에 따라 여러 유형으로 구분되며, 일반적으로 다음과 같은 방식으로 표현된다.

(1) Unigram (n=1)

• 개별 단어를 독립적으로 고려한다.
• 예시:

  "I love NLP" → ["I", "love", "NLP"]

(2) Bigram (n=2)

• 두 개의 연속된 단어를 조합한다.
• 예시:

  "I love NLP" → ["I love", "love NLP"]

(3) Trigram (n=3)

• 세 개의 연속된 단어를 조합한다.
• 예시:

  "I love NLP" → ["I love NLP"]

(4) 4-gram, 5-gram, ...

• 네 개, 다섯 개, 그 이상의 연속된 단어를 조합하여 구성할 수 있다. (위 예시에서는 전체 문장이 3 단어로 구성되어있기 때문에, 4-gram부터는 다루지 않았다)

2. Chain rule

---

n-gram 모델은 주어진 단어 시퀀스에서 다음 단어가 등장할 확률을 예측하는 역할을 한다. 이러한 확률을 계산하기 위해 Chain Rule(연쇄 법칙)을 사용한다.

2.1. Chain Rule이란?

Chain Rule은 연속된 단어들의 확률을 개별 조건부 확률로 분해하는 방법이다.

임의의 단어 시퀀스 $w_1, w_2, ..., w_n$가 주어졌을 때, 전체 문장의 확률은 다음과 같이 계산된다.

$P(w_1, w_2, ..., w_n) = P(w_1) \cdot P(w_2 | w_1) \cdot P(w_3 | w_1, w_2) \cdot ... \cdot P(w_n | w_1, w_2, ..., w_{n-1})$

즉, 각 단어의 출현 확률은 이전 단어들의 조합에 의해 결정된다는 개념이다.
($w_1$이 독립적으로 존재할 확률 $\times$ $w_1$이 등장했을때 $w_2$가 등장할 확률 $\times$ $\dots$)

2.2. 예제

문장: "The cat sat on the mat"
이 문장의 확률은 Chain Rule을 적용하면 다음과 같이 계산할 수 있다.

$P(\text{"the cat sat on the mat"}) = P(\text{"the"}) \cdot P(\text{"cat"} | \text{"the"}) \cdot P(\text{"sat"} | \text{"the cat"}) \cdot P(\text{"on"} | \text{"the cat sat"}) \cdot P(\text{"the"} | \text{"the cat sat on"}) \cdot P(\text{"mat"} | \text{"the cat sat on the"})$

이는 각 단어의 등장 확률이 앞의 모든 단어에 의해 결정됨을 의미한다.

이때 $P(w_i \mid w_1, \dots, w_{i-1})$를 직접 추정하기 위해서는 방대한 데이터가 필요하다. 왜냐하면 문장 길이가 길어질수록 이전 단어(맥락)가 기하급수적으로 많아지기 때문이다. 따라서 현실적으로는 모든 조건부 확률을 정확히 계산하기가 어려우며, 이를 단순화하기 위해 Markov Assumption(마르코프 가정)을 도입한다.

3. Markov Assumption(마르코프 가정)

---

3.1. Markov Assumption이란?

마르코프(마코프) 가정이란 현재 상태(단어)의 확률이 과거 전체가 아닌, 직전 k개의 상태(단어)에만 의존한다는 개념이다.
즉, 긴 문맥을 고려하지 않고 최근의 정보만 반영하여 다음 단어의 확률을 예측하는 방식이다.

이를 통해 확률 모델의 계산 복잡도를 줄이고, 보다 실용적인 방식으로 학습할 수 있다.

• 모델 복잡도 감소:
  전체 문장을 고려하는 것보다 최근 k개 단어만 고려하는 것이 연산량을 크게 줄일 수 있음.
• 학습이 용이:
  마코프 가정을 적용하면 모든 단어의 조합을 학습할 필요 없이 k-gram만 저장하면 되므로 데이터가 적을 때도 학습이 가능.

3.2. k-th-order Markov Model

k-th model을 살펴보기에 앞서어 1차 Markov Model부터 차근차근 살펴보도록 하자.

< 1st-order Markov Model >

• 1st-order Markov Model은 가장 단순한 형태로, 현재 단어는 직전 단어(1개)만 고려하여 예측한다고 가정한다.

• 확률 계산식:

  $P(w_n | w_1, w_2, ..., w_{n-1}) \approx P(w_n | w_{n-1})$

• 예제:

  $P(\text{"mat"} | \text{"the cat sat on the"}) \approx P(\text{"mat"} | \text{"the"})$

  즉, "mat"이라는 단어가 등장할 확률은 전체 문장이 아니라 바로 앞 단어 "the"에 의해서만 결정된다는 가정이다.

< 2nd-order Markov Model >

• 현재 단어는 직전 두 개의 단어에 의해서 결정된다고 가정한다.

• 확률 계산식:

  $P(w_n | w_1, w_2, ..., w_{n-1}) \approx P(w_n | w_{n-2}, w_{n-1})$

• 예제:

  $P(\text{"mat"} | \text{"the cat sat on the"}) \approx P(\text{"mat"} | \text{"on the"})$

  즉, "mat"이 등장할 확률은 전체 문장이 아니라 직전 두 단어인 "on the"에 의해 결정된다는 가정이다.

< k-th-order Markov Model >

• 현재 단어가 k개의 이전 단어에 의존한다고 가정하는 확장된 모델이다.

• 확률 계산식:

  $P(w_i | w_1, w_2, ..., w_{i-1}) \approx P(w_i | w_{i-k}, ..., w_{i-1})$

• 즉, 전체 문맥을 고려하지 않고, 최근 k개의 단어만 반영하여 다음 단어의 확률을 추정한다.

• 문장 확률 계산:

  $P(w_1, w_2, ..., w_n) \approx \prod_{i} P(w_i | w_{i-k}, ..., w_{i-1})$

• n-gram 모델에서 $k = n-1$로 설정하면 k-th order Markov Model과 동일한 형태가 된다.

3.5. Markov Assumption을 적용한 n-gram 모델

• unigram (k=0): 이전 단어의 영향을 전혀 고려하지 않음.

  $P(w_n) = P(w_1) P(w_2) P(w_3) ... P(w_n)$

• bigram (k=1): 직전 한 개의 단어만 고려.

  $P(w_n | w_1, ..., w_{n-1}) \approx P(w_n | w_{n-1})$

• trigram (k=2): 직전 두 개의 단어만 고려.

  $P(w_n | w_1, ..., w_{n-1}) \approx P(w_n | w_{n-2}, w_{n-1})$

• k-gram: 직전 $k$개의 단어만 고려.

  $P(w_n | w_1, ..., w_{n-1}) \approx P(w_n | w_{n-k}, ..., w_{n-1})$

4. n-gram 모델에서의 확률 추정

---

4.1. 최대우도추정(MLE) 방식

통상적으로 n-gram 모델은 코퍼스(훈련 데이터)에서 등장 빈도를 세어 확률을 추정한다. 예를 들어 빅그램일 때,

$P(w_i \mid w_{i-1}) = \frac{\text{count}(w_{i-1}, w_i)}{\text{count}(w_{i-1})}.$

• $\text{count}(w_{i-1}, w_i)$는 두 단어 $(w_{i-1}, w_i)$가 연속해서 등장한 횟수이다.
• $\text{count}(w_{i-1})$는 단어 $w_{i-1}$가 코퍼스 전체에서 등장한 횟수이다.

이처럼 빈도 기반 추정은 간단하면서도 효과적이지만, 데이터가 제한적일 경우 특정 n-gram이 전혀 등장하지 않으면 해당 확률이 0으로 계산된다.

4.2 희소성(Sparsity) 문제

자연어는 어휘가 방대하고, 실제로 관측되지 않는 n-gram 조합이 매우 많다. 코퍼스가 유한한 크기이므로, 관측되지 않은 n-gram에 확률 0을 부여하는 건 모형 일반화를 저해한다. 따라서 이를 해결하기 위한 스무딩(smoothing) 전략이 필수적으로 활용된다.

스무딩을 알아보기에 앞서 먼저 Perplexity를 알아보자.

5. Perplexity

---

5.1. Perplexity란?

Perplexity(ppl.)는 언어 모델이 주어진 단어 시퀀스를 얼마나 잘 예측하는지를 평가하는 척도이다. 확률적으로 모델이 어떤 문장을 얼마나 자연스럽게 생성할 수 있는지를 수치로 표현하며, 낮을수록 모델의 성능이 좋음을 의미한다.

Perplexity는 주어진 코퍼스(데이터셋)에서 단어 시퀀스의 확률을 기반으로 정의된다.

$Perplexity = P(w_1, w_2, ..., w_n)^{-\frac{1}{n}}$

즉, n개의 단어가 등장할 확률을 기반으로, 해당 모델이 다음 단어를 얼마나 혼란 없이 예측할 수 있는지를 나타낸다.

Perplexity의 핵심 개념은 확률이 높을수록 perplexity가 낮아지며, 확률이 낮을수록 perplexity가 증가한다. 즉, 언어 모델이 더 자연스러운 문장을 생성할수록 perplexity 값이 낮아지고, 불확실성이 높은 모델일수록 perplexity 값이 높아진다.

5.2. Perplexity와 Cross-Entropy

Perplexity는 크로스 엔트로피(Cross-Entropy)와 밀접한 관련이 있다. 크로스 엔트로피는 (기존에 계속해서 봐왔다시피) 모델이 실제 데이터 분포를 얼마나 잘 예측하는지를 측정하는 지표이며, 다음과 같이 정의된다.

$H(P) = - \frac{1}{n} \sum_{i=1}^{n} \log P(w_i | w_1, ..., w_{i-1})$

Perplexity는 크로스 엔트로피의 지수(exp) 값으로 표현되며, 다음과 같은 관계가 성립한다.

$Perplexity = e^{H(P)}$

즉, Perplexity를 최소화하는 것은 곧 크로스 엔트로피를 최소화하는 것과 동일하며, 이는 모델이 예측한 확률 분포가 실제 데이터 분포와 가까워지는 것을 의미한다.

따라서 Perplexity를 낮추는 것은 언어 모델의 성능을 향상시키는 중요한 목표가 된다.

5.3. Perplexity의 직관적 이해

Perplexity를 직관적으로 이해하려면, 어휘 크기(Vocabulary Size)와의 관계를 고려할 수 있다.

어떤 k-gram 모델이 존재하고, 주어진 단어가 등장할 확률이 모든 단어에 대해 동일하게 분포한다고 가정하면,

$P(w | w_{i-k}, ..., w_{i-1}) = \frac{1}{|V|}$

따라서 가능한 모든 단어가 균등한 확률을 가지는 경우에, Perplexity는 다음과 같이 나오게 된다.

$Perplexity = e^{H(P)} = |V|$

즉, 모든 단어가 균등한 확률로 등장한다면, Perplexity 값은 어휘 크기(V)와 동일하다. 이는 Perplexity가 언어 모델이 단어를 얼마나 잘 예측하는지에 대한 상대적인 지표임을 보여준다.

예를 들어, 단어 분포가 균등한 경우(=예측이 전혀 불가능한 경우), Perplexity는 어휘 크기 자체와 같아진다. 반면, 언어 모델이 단어를 매우 잘 예측할 수 있다면 Perplexity는 이보다 훨씬 작은 값이 될 것이다.

6. Smoothing

---

6.1. Smoothing의 필요성과 희소성 문제

n-gram 모델을 활용한 언어 모델은 특정 단어 시퀀스의 확률을 학습된 데이터(코퍼스)에서 추정하여 다음 단어를 예측한다. 그러나 실험 환경이거나 새로운 테스트 셋에서는 기존의 학습 데이터에 존재하지 않는 새로운 n-gram이 등장하는 경우가 잦으며, 이때 해당 확률이 0(zero probability)가 되는 문제가 발생한다. 이를 우리는 희소성(Sparsity)문제 라고 한다.

이러한 문제를 해결하기 위해 Smoothing이 필요하다. Smoothing은 데이터에서 관측되지 않은 n-gram의 확률을 보정하여, 모델이 더 일반화된 언어 확률을 학습할 수 있도록 돕는 방법이다.

예제:

• 훈련 데이터(training corpus):
• 테스트 데이터(test corpus): 성학십도(聖學十圖) by 퇴계이황
  
  이 경우, 성학십도의 단어 조합이 Naver News에 포함되지 않았을 가능성이 높으며, 이로 인해 해당 n-gram의 확률이 0이 될 수 있다.
  
  $P(\text{"tax"} | \text{"성학"}) = 0$
  
  이러한 확률이 0이 되면 전체 문장의 확률 또한 0이 되어 perplexity를 정의할 수 없는 문제가 발생한다.

6.2. Zipf의 법칙

자연어는 Zipf의 법칙(Zipf’s Law)을 따른다. Zipf의 법칙에 따르면, 빈도가 높은 단어는 매우 자주 등장하지만, 빈도가 낮은 단어는 거의 등장하지 않는다. 즉, 대부분의 단어는 매우 낮은 빈도로 등장하며, n-gram 모델에서는 이러한 단어들의 확률을 적절히 처리해야 한다.

예를 들어,

• "the", "and", "of"와 같은 단어는 매우 높은 빈도를 보인다.
• 그러나 일부 희귀한 단어는 특정 문서에서만 등장하며, 이는 학습 데이터에서 충분히 관측되지 않을 가능성이 높다.

이로 인해 희귀 단어 조합이 등장했을 때 확률이 0이 되지 않도록 하는 것이 스무딩의 핵심 목표이다.

6.3. Smoothing 기법

Smoothing 기법에는 다양한 방법이 존재하며, 각각의 방식은 확률을 보정하는 방식이 다르다. 우리는 대표적으로

(1) Additive(=Laplace) Smoothing
(2) Discounting(Absolute Discounting)
(3) Interpolation(Linear Interpolation)

을 자세히 설명해보도록 하겠다.

6.3.1. Additive Smoothing (Laplace Smoothing)

개념

• 가장 간단한 smoothing 방법 중 하나로, 모든 가능한 n-gram의 빈도수(count)에 일정한 값을 더하는 방식이다.
• Add-one Smoothing 또는 Laplace Smoothing이라고도 불린다.
• 모든 확률이 0이 되는 것을 방지하는 것이 목표이며, 다음과 같은 방식으로 확률을 보정한다.

공식

기존 bigram 확률의 최대우도 추정(Maximum Likelihood Estimation, MLE) 식:

$P(w_i | w_{i-1}) = \frac{C(w_{i-1}, w_i)}{C(w_{i-1})}$

위와 같이 단순히 빈도수를 확률로 변환하면, 한 번도 등장하지 않은 n-gram의 확률이 0이 되는 문제가 발생한다. 이를 해결하기 위해 모든 n-gram의 빈도에 α를 더하고, 이를 다시 정규화한다.

$P(w_i | w_{i-1}) = \frac{C(w_{i-1}, w_i) + \alpha}{C(w_{i-1}) + \alpha |V|}$

여기서:

• $C(w_{i-1}, w_i)$ : bigram $((w_{i-1}, w_i)$의 등장 횟수
• $C(w_{i-1})$ : $w_{i-1}$이 등장한 총 횟수
• $|V|$ : 전체 어휘 크기(vocabulary size)
• $\alpha$ : 작은 양수(일반적으로 $\alpha = 1$, 따라서 Add-One Smoothing이라고도 함)

• 장점: 매우 간단하고 구현이 쉬움.
• 단점: 실제 데이터에서 빈도수가 높은 단어에도 동일한 smoothing이 적용되어 과대평가될 수 있음.
  즉, 낮은 빈도의 단어는 과소평가되고, 높은 빈도의 단어는 과대평가되는 문제가 발생.

6.3.2. Discounting (절대 할인, Absolute Discounting)

개념

• Discounting 기법은 빈도수가 높은 n-gram에서 일부 확률 질량(probability mass)을 제거하여 학습되지 않은 n-gram에 분배하는 방식이다.
• 확률을 보존하면서도 희소한 n-gram에 더 많은 확률을 할당하는 방법이다.

Absolute Discounting 공식
Absolute Discounting에서는 각 빈도에서 특정 상수 $d$를 빼줌으로써 보정한다.

$P_{\text{abs-discount}}(w_i | w_{i-1}) = \begin{cases} \frac{C(w_{i-1}, w_i) - d}{C(w_{i-1})} & \text{if } C(w_{i-1}, w_i) > 0 \\ \alpha(w_{i-1}) P(w_i) & \text{if } C(w_{i-1}, w_i) = 0 \end{cases}$

여기서:

• $d$는 discounting 값(일반적으로 $d < 1$)
• $\alpha(w_{i-1})$는 확률 질량을 조정하는 스케일링 계수
• $P(w_i)$는 unigram 확률(단어 자체의 출현 확률)

이 방식에서는 빈도수(count)가 0인 n-gram에 대해 전체적인 확률 질량을 분배하며, 기존에 등장한 n-gram의 확률을 일부 할인(discount)하여 희소한 n-gram이 확률을 가질 수 있도록 한다.

특징

• 장점: 빈도수에 따라 할인 정도를 조절할 수 있어 현실적인 smoothing 방법.
• 단점: 할인 값 $d$를 적절히 선택해야 하며, 데이터셋에 따라 다르게 설정해야 할 수도 있음.

6.3.3. Linear Interpolation (선형 보간법)

개념

• Interpolation(보간법)은 다양한 n-gram 모델을 결합하여 확률을 추정하는 방식이다.
• 단순히 특정 n-gram만 사용하는 것이 아니라, unigram, bigram, trigram 등 여러 개의 n-gram 모델을 조합하여 하나의 확률을 계산한다.
• 이를 통해 더 많은 문맥 정보를 반영하고, 희소성을 완화할 수 있다.

공식

$\hat{P}(w_i | w_{i-2}, w_{i-1}) = \lambda_1 P(w_i | w_{i-2}, w_{i-1}) + \lambda_2 P(w_i | w_{i-1}) + \lambda_3 P(w_i)$

여기서:

• $P(w_i | w_{i-2}, w_{i-1})$ : trigram 확률
• $P(w_i | w_{i-1})$ : bigram 확률
• $P(w_i)$ : unigram 확률
• $\lambda_1, \lambda_2, \lambda_3$ : 보간 가중치 (이들의 합은 1이 되어야 함, $\sum \lambda_i = 1$)

Lambda 값 설정 방법

• 먼저 훈련 데이터(training set)에서 n-gram 확률을 추정.
• 이후 개발 데이터(validation set)에서 $\lambda$ 값을 최적화.
• 최적의 $\lambda$를 찾은 후, 이를 테스트 데이터(test set)에서 평가.

특징

• 장점: 여러 개의 n-gram을 결합하여 보다 정교한 확률 추정 가능.
• 단점: $\lambda$ 가중치를 설정하는 과정이 필요하며, 최적값을 찾기 위해 개발 데이터가 필요함.

7. n-gram 모델의 한계

---

• 장거리 의존 추적 한계: n-gram은 결국 최대 $n-1$개 단어 앞까지만 본다. 문장 내 후반부를 결정하는 데 문맥 전반이 크게 작용하는 경우, n-gram은 충분히 반영하기 어렵다.

• 데이터 희소성: $n$이 커질수록 필요한 코퍼스 크기가 기하급수적으로 늘어난다. 충분한 데이터를 확보하지 못하면 대부분의 n-gram이 관측 빈도가 극도로 낮아지거나 0이 되어, 모델이 제대로 학습되지 않는다.

이런 한계 때문에 현대의 언어 모델은 RNN, LSTM, 트랜스포머(Transformer) 같은 신경망 구조를 활용하는 추세이다. 그러나 n-gram 모델은 개념이 단순해 이해하기 쉽고, 특정 제한적 환경(낮은 자원)에서 여전히 활용될 수 있다. 또한 머신러닝 및 NLP 교육 과정에서, 확률적 언어 모델을 배우는 데 훌륭한 기초 역할을 하며, 대학강의나, 기초수업에서 초반부분에 필수적으로 다뤄지고 있다.

8. Reference

---

[1] Machine Learning - N-gram이란 무엇인가? 텍스트 분석의 핵심 이해하기

• https://datasciencebeehive.tistory.com/114

[2] 딥 러닝을 이용한 자연어 처리 입문 : 03-03 N-gram 언어모델(N-gram Language Model)

• https://wikidocs.net/21692

[3] 딥 러닝을 이용한 자연어 처리 입문 : 03-05 펄플렉서티(Perplexity, PPL)

• https://wikidocs.net/21697