이 글은 부스트캠프 AI Tech 3기 강의를 듣고 정리한 글입니다.
요약
- Content-based 는 TF-IDF를 활용해 Item Profile을 만든다.
- User와 Item 간의 유사도를 계산하여 Top-K 추천을 할 수 있다.
- 새로운 아이템에 대해서는 유저가 선호한 아이템에 대한 새로운 아이템의 유사도를 가중치로 두고 가중치평균을 구하게 되면 평점을 예측할 수 있다.
Content-based Recommendation
유저 x가 과거에 선호한 아이템과 비슷한 아이템을 유저 x에게 추천
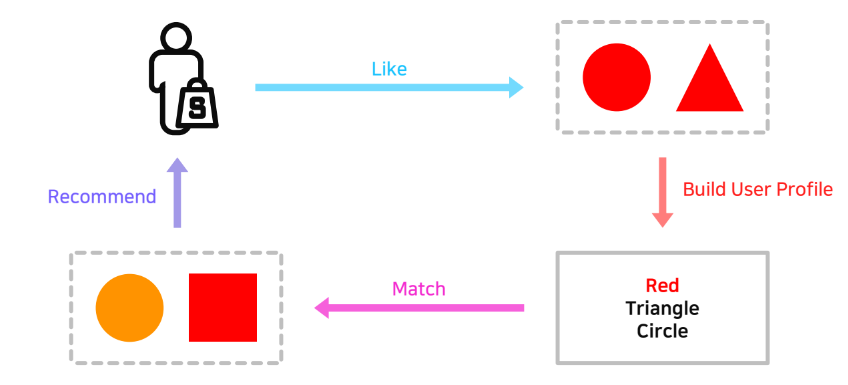
컨텐츠 기반 추천의 장점과 단점은 서로 연결되어 장점이 단점이 되기도 한다.
장점
- 유저에게 추천을 할 다른 유저 데이터 필요하지 않음
- 새로운 아이템 or 인지도 낮은 아이템 추천 가능
- 추천 아이템에 대한 설명가능
단점
- 아이템의 적합한 feature 찾기 어려움 (가장 어려운 문제)
- 한가지 분야/장르의 추천 결과만 계속 나올 수 있음(overspecialization)
- 다른 유저의 데이터 활용 불가능
위 그림에서 Profile이란 item의 feature들이다.
예시) (item) A영화 -> (profile) 감독, 장르, 출연배우
이런 아이템이 가진 feature들은 Vector 형태로 보통 표현 하게 되는데 이를 TF-IDF에 적용해보자.
TF-IDF
우선 TF-IDF 가 무엇인지 알아보자.
TF-IDF(Term Frequency-Invese Document Frequency)는 말 그대로 단어(Term)이 문서(Document)에 얼마나 자주 나타나는가(Frequency)를 나타내어 단어의 중요도를 나타내는 스코어이다.
문서의 경우 중요한 단어들의 집합으로 표현할 수 있는데, 이때 중요한 단어들을 선정하는 스코어 중 가장 기본적이고 많이 쓰는 방법은 TF-IDF이다.
조금 더 자세히 살펴보면
- 문서d에 등장하는 단어w에 대해서
- 단어w가 문서d에 많이 등장하면서(TF)
- 단어w가 전체문서D에서는 적게 등장하는 단어라면 (IDF)
- 단어w는 문서d를 설명하는 중요한 feature로 TF-IDF값이 높다.
수식으로 살펴보자
-
TF : 단어w가 문서d에 등장하는 횟수
여기서 두번째 식은 가장 많이 등장한 단어로 나눠줘 Normailzation을 하는 것이다.
-
IDF : 전체 문서 가운데 단어 w가 등장한 비율의 역수 (단어마다 정의)
IDF 값의 변화가 크기 때문에 smoothing을 위해 log 사용
-
최종 TF-IDF
최종적으로 TF-IDF는 앞서 구한 TF와 IDF의 곱으로 구해진다.
예시를 보면 다음과 같다.
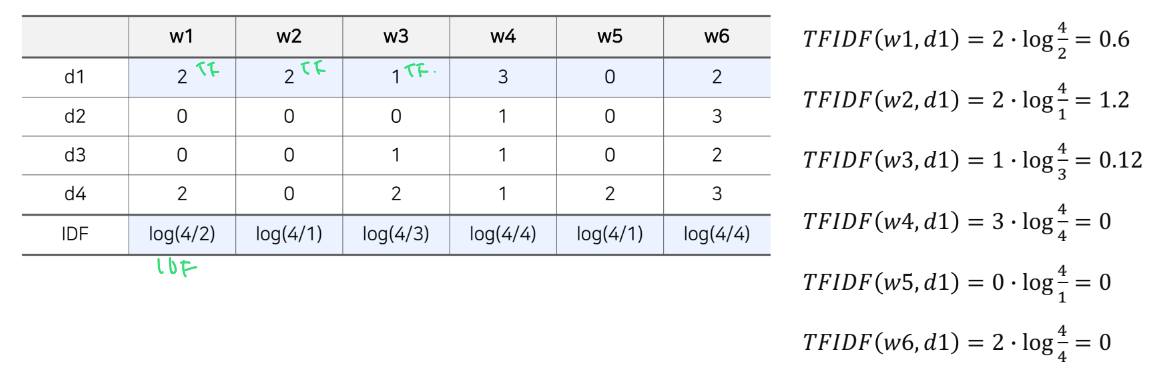
이렇게 구한 값을 다시 표에 대입하면 document의 TF-IDF vector를 구할 수 있다.
여기서는 6개의 단어가 있어 6차원의 vector로 표현된다.

->여기서 문서를 Item으로 보고, 단어를 Item의 feature로 보면 위 예시에서 구한 vector는 item의 feature vector로 볼 수 있다.
: Item 1의 feature vector (feature는 6개)
User Profile 기반 추천
Item Profile을 모두 구축했으니 우리가 할 일은 User Profile을 구축하여 유저에게 아이템을 추천해 주는 것이다.

User Profile 은 어렵지 않게 만들 수 있다.
- 유저가 과거에 선호했던 Item List가 있고 각 아이템은 TF-IDF를 통해 Vector로 표현 (위에서 진행한 TF-IDF)
- 각 유저의 Item List 안에 있는 Item Vector들을 통합
->User Profile생성
이때 Item Vector들을 통합하는 방법에는 2가지가 있다.
-
Simple : 유저가 선호한 Item Vector들의 단순 평균
-
Variant : 유저가 아이템에 내린 선호도로 정규화한 평균값 사용
이렇게 User Profile을 만들어서 유저와 아이템의 유사도를 계산한다.
※ Content-based 는 유저간 유사도가 아님을 유의하자!
이때 유사도는 Cosine 유사도를 사용한다.
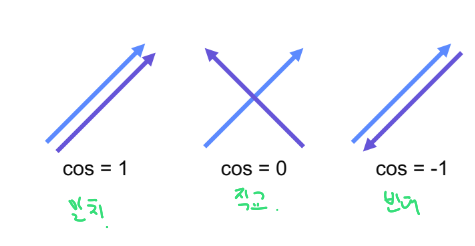
주의할 점은 두 벡터의 차원이 동일해야 한다는 점이다.
위 Cosine 유사도 개념을 적용하여 유저와 아이템의 각도(얼마나 비슷한지)가 얼마나 차이나는지 계산한다
둘의 유사도가 클수록 해당 아이템이 유저에게 관련성이 높다는 것이고
추천을 할 때는 유사도가 높은순으로 추천(Top-K 추천)하게 된다.
Rating 예측
여기서 Rating 까지 예측할 순 없을까 의문이 든다.
유저가 선호하는 아이템의 Vector를 활용하여 새로운 item의 평점을 예측해보자.
우선 새로운 아이템 와 유저가 선호하는 아이템집합에 속한 아이템 의 유사도를 구한다.
이 유사도를 가중치로 사용하여 의 평점을 추론
