Simple Linear Regression

• 독립 변수가 하나인 경우 단순회귀분석(Simple Linear Regression)이라 한다.

Best-Fit Line

• 실제 점들(실측값) 사이의 거리를 고려하여 생성되어야 함.
• best-fit line과 예측된 점들(예측값)들간의 거리는 오차(error)이다.

직선의 방적식 (The equation of line)

• $a : 기울기(slope)$
• $b : y절편(y-intercept)$

평균 제곱 오차 (MSE:Mean Squared Error)

• MSC(Mean Squared Error) : 평균 제곱 오차

  $MSE = \frac{1}{n} \sum_{i=1}^n (y_i - \tilde{y_i})^2$

• $y_i : 예측값$

• $\tilde{y_i} : 실측값$

• 1차 정리

  $MSE = (y_1 - (ax_1+b))^2+(y_2-(ax_2+b))^2+...+ (y_n-(ax_n+b))^2$

• 2차 정리

  $MSE = y_1^2 - 2y_1(ax_1+b) + (ax_1+b)^2+...+ y_n^2-2y_n(ax_n+b)+(ax_n+b)^2$

• 3차 정리 (괄호 풀기)

  $MSE = y_1^2-2y_1ax_1-2y_1b+a^2x^2+2ax_1b+b^2+...+y_n^2-2y_nax_n-2y_nb+a^2x_n^2+2ax_n+b+b^2$

• 4차 정리

  $MSE = (y_1^2+...+y_n^2)-2a(x_1y_1+...+x_ny_n)-2b(y1+...+y_n)+a^2(x_1^2+...+x_n^2)+2ab(x_1+...+x_n)+nb^2$

• $y,xy,x,x^2$의 모든 제곱값의 평균을 취함

  $\bar{y^2}=\frac{y_1^2+y_2^2+...+y_n^2}{n}$

• 방정식의 양쪽을 n으로 곱하여 다음을 얻는다.

  $\bar{y^2}n = y_1^2+y_2^2+...+y_n^2$

최종 MSE 공식

MSE함수를 최소화하는 a(기울기)와b(y-절편)를 구하는 것이 목표임.
👉🏻 a에 대한 편미분, b에 대한 편미분 수행
👉🏻 최소점(Global Minima)를 찾고있으므로 편미분을 취하고 0과 비교함

편미분 공식

편미분 공식 적용

방정식 빼기

• 해당 방정식에서 분모를 없애봄
  $a= \frac{\bar{y}-\frac{\bar{xy}}{\bar{x}}}{\bar{x}-\frac{\bar{x^2}}{\bar{x}}} ∗ \frac{\bar{x}}{\bar{x}} =\frac{\bar{x}\bar{y}-\bar{xy}}{(\bar{x})^2-\bar{x^2}}$

📌 a(기울기) 최종 방정식

$a=\frac{\bar{x}\bar{y}-\bar{xy}}{(\bar{x})^2-\bar{x^2}}$

📌 b(y-절편) 최종 방정식

$b=\bar{y}-a\bar{x}$

📌 $\bar{x}$ 최종 공식

$\bar{x}=\frac{x_1+x_2+..+x_n}{n}$

📌 $\bar{x^2}$ 최종 공식

$\bar{x^2}=\frac{x_1^2+x_2^2+..+x_n^2}{n}$

📌 $\bar{xy}$ 최종 공식

$\bar{xy}=\frac{x_1y_1+x_2y_2+...+x_ny_n}{n}$

📌 $\bar{y}$ 최종 공식

$\bar{y}=\frac{y_1+y_2+...+y_n}{n}$

Global Minima

• 오류가 최소가 된 곳
• 오차(Error)를 최소화하는 M(기울기)와 B(y절편)을 찾아야 함.

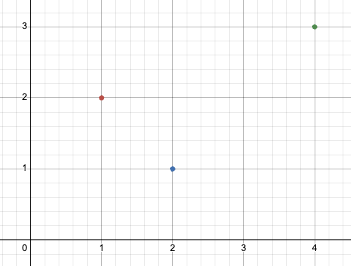
Example 1

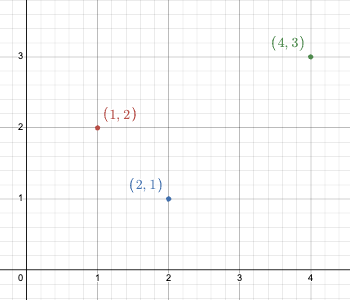
• 3 points
  (1,2),(2,1),(4,3)

Example 1 예제 - $\bar{x}$ 구하기

• $\bar{x} = \frac{1+2+4}{3}=\frac{7}{3}$

Example 1 예제 - $\bar{y}$ 구하기

• $\bar{y} = \frac{2+1+3}{3}=\frac{6}{3}=2$

Example 1 예제 - $\bar{xy}$ 구하기

• $\bar{xy} = \frac{1*2+2*1+4*3}{3}=\frac{16}{3}$

Example 1 예제 - $\bar{x^2}$ 구하기

• $\bar{x^2} = \frac{1^2+2^2+4*2}{3}=\frac{21}{3}=7$

Example 1 예제 - a, b 방정식에 대입

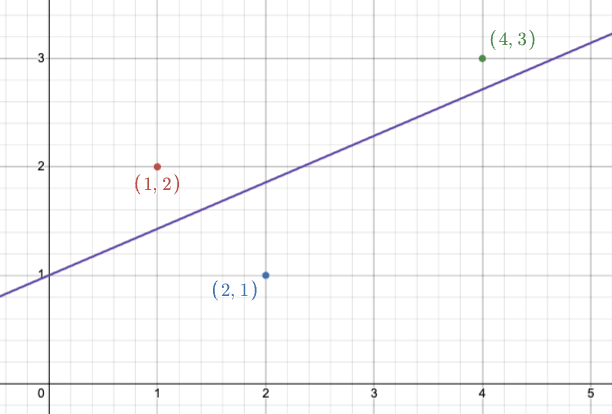
🔥 Example 1 예제 - 최종 대입 결과

Example 2

• 4 points
  (-2,-3),(-1,-1),(1,2),(4,3)
  

Example 2 예제 - $\bar{x}$ 구하기

• $\bar{x} = \frac{(-2)+(-1)+1+4}{4}=\frac{1}{2}$

Example 2 예제 - $\bar{y}$ 구하기

• $\bar{y} = \frac{(-3)+(-1)+2+3}{4}=\frac{1}{4}$

Example 2 예제 - $\bar{xy}$ 구하기

Example 2 예제 - $\bar{x^2}$ 구하기

• $\bar{x^2} = \frac{4+1+1+16}{4}=\frac{11}{2}$

Example 2 예제 - a, b 방정식에 대입

🔥 Example 2 예제 - 최종 대입 결과