문제 난이도에 비해서 좀 오래 헤맸다...
잘 이해가 안돼서 풀어 써 보려고 한다. 이해가 될 때까지...
고민하기
이 문제는 dp 문제다. 부분 문제의 해답으로 전체 문제의 해답을 유도할 수 있다.
dp 문제라는 걸 알기 전까지 (풀다가 안 풀려서 문제 유형 뜯어보고 알았다) 일반식을 만들어셔 풀려고 했다.
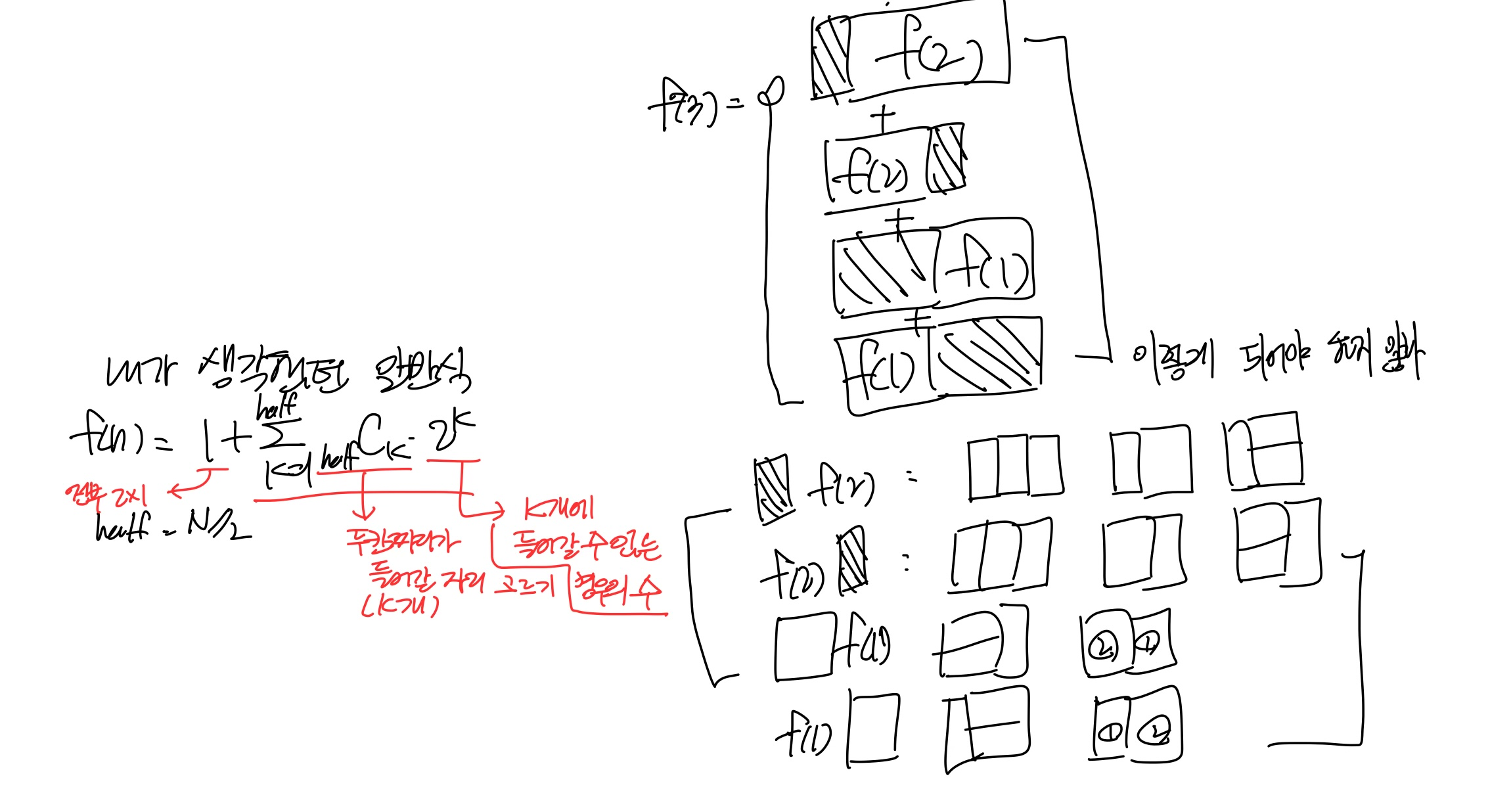
내가 생각했던 일반식은 아래와 같다:
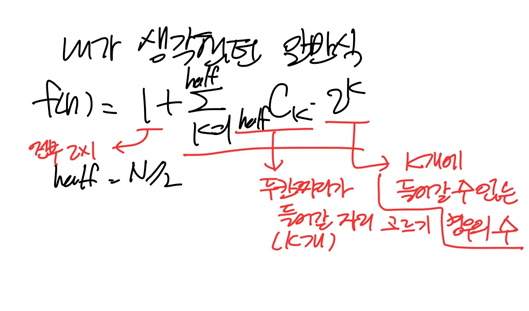
크게 두 부분으로 나뉘어진다.
(1) 1: 전체가 2x1인 경우를 뜻함
(2) 두 칸 짜리 (1x2, 2x2)가 들어갈 자리를 고르고, 각 자리에 들어갈 경우의 수를 고르는 부분
- 여기서 조합을 사용하는데, itertools의 combination을 슬쩍 보니까 iteratable한 객체의 ㄹㅇ 조합 가능한 경우를 다 털어주는 메소드길래... len() 쓰면 될 것도 같았지만 시간이 무쟈게 오래 걸릴 것 같아서 팩토리얼로 구현했었다.
- 문제는 이렇게 풀면 진짜 으마으마하게 큰 수가 나온다. 솔직히 이게 왜 틀린 답인지 아직 이해 못했다. 숫자와 그림 사이에 매핑이 잘 안된다...
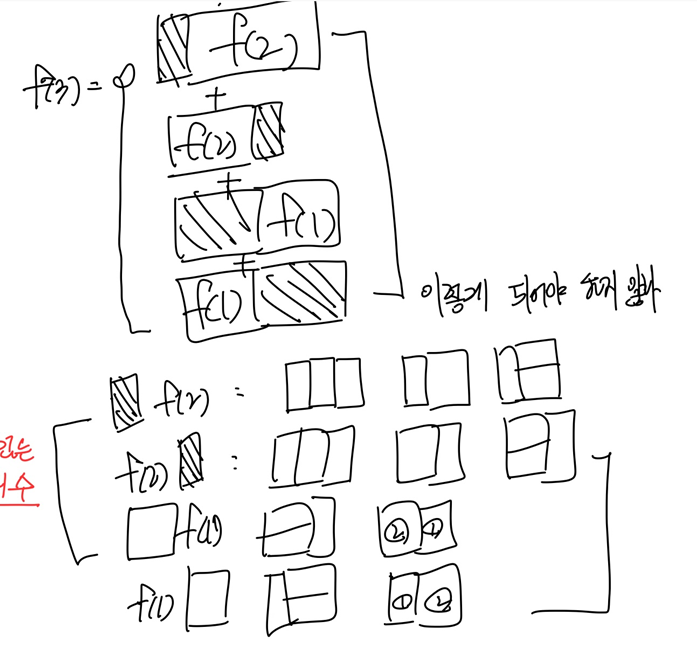
이 문제의 실제 해답은 이렇다: f(n) = 2 * f(n-2) + f(n-1) (when n >= 3)
- 전체에 2칸짜리를 넣었을 때 남는 경우의 수 f(n-2), 1x2 두 개로 채우는 경우와 2x2 하나로 채우는 경우, 두 가지 경우의 수가 있으므로 2를 곱한다
- 전체에 한 칸짜리를 넣었을 때 남는 경우의 수 f(n-1)
- 이 둘을 합해서 답을 얻는다.
내가 이해 못한 부분
전체에 x(x=1, 2)칸짜리를 하나 집어넣으면 앞에 넣을지 뒤에 뒤에 넣을지 중간에 넣을지 결정해야 하지 않나?
그래서 f(3)의 경우의 수를 그려 봤다. 근데 놀랍게도... 2 * f(1)와 f(2)는 연결해놓은 대로라면 서로 중복되지 않는다.
쓰면서 생각난 건데 f(n-1)과 2x1의 위치 관계를 고려하지 않아도 되는 이유는 f(n-1)과 f(n-2)에서 이미 고려되어 있기 때문인 것 같다.
먼저 부분 문제의 정답으로 등록되어 있는 애들은 블록 간의 위치 관계를 모두 고려한 정답을 가지고 있다. f(1)과 f(2)를 그냥 상수값으로 미리 넣어두니까...
f(3)을 그림으로 표현한 것에서 확인할 수 있듯이 f(3)에는 2 * f(1)과 f(2) 에서 f(2)와 2 * 1의 위치 관계를 고려한 경우의 수가 모두 포함되어 있다.
그러면 f(4)는 f(3)의 타일 배열과 다른 타일의 위치 관계를 고려하지 않아도 된다. (셀 필요 없다는 뜻, 어차피 이미 고려되어 있으니까)
나아가서 f(n)에서는 f(n-1)과 다른 타일의 위치 관계를 고려할 필요가 없다. 그래서 저렇게 단순한 점화식을 얻어낼 수가 있다. (조합으로 자리 넣고 이런 짓하지 않아도...)
신기하네
세상은 정말 넓고 똑똑한 사람은 많고 갈 길은 멀구나