난리 바가지
회의실 배정
https://www.acmicpc.net/problem/1931
풀이
- 주어진 회의 시간을 끝나는 시간 기준으로 & 끝나는 시간이 같다면 시작하는 시간을 기준으로 정렬한다.
- 마지막으로 회의가 끝난 시간과 가장 가까운 시간에 시작하는 회의를 선택 (여러 개 있으면 짧은 것을 선택함)
- 마지막 회의가 끝난 시간을 갱신, 2로 돌아감
import sys
N = int(sys.stdin.readline())
timeTable = []
answer = 0
for _ in range(N):
a, b = map(int, sys.stdin.readline().split())
timeTable.append((a,b))
timeTable.sort(key=lambda x:(x[1], x[0]))
last = 0
for elem in timeTable:
if elem[0] >= last:
last = elem[1]
answer += 1
print(answer)왜 이렇게 풀어야 할까?
지금은 일단... 많은 문제를 접하고 생각해 보기 위해서 한 문제를 진득하게 풀기 보다는 좀 생각해 보고 각 안 나오면 질문 게시판을 뒤져보는 식으로 풀고 있다.
이 문제는 좀 뒤적거리다가 풀이가 생각이 잘 안 나길래 질문 게시판을 봤다. 슥슥 읽다가 시작 시간이 이른 순/끝나는 시간이 늦은 순... 이런 키워드를 보고 슉슉 풀었다. 그래서 왜 회의 시간을 정렬해야 되는지 이해를 못했다. 이런 괴랄한 풀이도 탄생시켰다.
풀이 1: 틀렸습니다
import sys
N = int(sys.stdin.readline())
timeTable = []
answer = 0
for _ in range(N):
a, b = map(int, sys.stdin.readline().split())
timeTable.append((a,b))
timeTable.sort(key=lambda x:(x[1], x[0]), reverse=True)
last = 2 ** 31
for elem in timeTable:
if elem[1] <= last:
last = elem[0]
answer += 1
print(answer)
풀이 2: 시간 초과
import sys
N = int(sys.stdin.readline())
timeTable = []
answer = 0
for _ in range(N):
a, b = map(int, sys.stdin.readline().split())
timeTable.append((a,b))
timeTable.sort(key=lambda x:(x[1], x[0]), reverse=True)
# 늦게 끝나는 회의부터 주머니에 넣을 것이다 (reverse=True)
start = 0
while start < N:
last = 2 ** 31
# 마지막으로 선택한 회의가 끝나는 시간
# 문제에서 시간은 최대 2^31 -1 의 값을 갖는다고 하였으므로...
temp = timeTable[start:]
# 이런 식으로 풀게 된 이유는... 아래 반례에서 따로 설명함
thisAnswer = 0
for elem in temp:
if elem[1] <= last:
last = elem[0]
thisAnswer += 1
answer = max(answer, thisAnswer)
# slicing해서 찾은 답과 지금까지의 답 중 큰 값을 answer에 넣는다
start += 1
if N - start <= answer:
# 만약 다음에 돌리려는 리스트의 크기가 answer보다 작으면 어차피 answer 이상의 값을 얻을 수 없다. => break
break
print(answer)슬픈 풀이의 원인
- 원래의 풀이 (늦게 끝나는 회의부터, 끝나는 시간이 같으면 시작하는 시간이 늦은 것부터 선택)에서는 아래와 같은 반례를 해결할 수 없었다:
- 6 / 1 10 / 2 3 / 4 5 / 6 7 / 8 9 / 10 11
- 답은 5 (1 10 제외한 나머지를 선택)
- 하지만 슬픈 while문을 돌지 않으면 뒤에서부터 고르기 때문에 답이 1이 된다.
- 이것을 해결하기 위해 리스트를 하나씩 slicing해가면서 답을 찾도록 했다.
- 결과적으로 여러 반례를 해결했으나 IDE에서는 영원히 돌아가는 테케들이 있었고 백준에서는 시간 초과가 나오게 된다.
그래서 구글링을 했어요
회의실 배정 문제는 그리디 알고리즘의 대표적인 문제라고 한다. 그래서 꼭 백준의 이 문제가 아니더라도 그리디 알고리즘을 이해하기 위해 이론적으로 설명해둔 자료들이 많았다. 여기저기 찾아보고 좀 쳐다본 내용을 정리해 보려고 한다.
가장 기본적인 대전제는 이것이다:
같은 시간표를 가지고 있다면, 더 긴 시간을 쓸 수 있을 때 더 많은 회의를 진행시킬 수 있다.
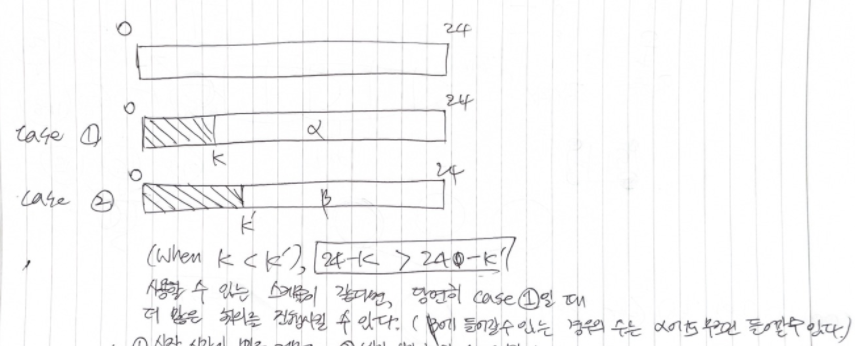
0시부터 24시까지 진행할 수 있는 회의 수의 최댓값을 구하려고 한다.
만약 0시부터 K시, K`시까지 진행하는 어떤 회의가 각각 있다고 생각하자. K < K`이라면, 24 - K > 24 - K`이 된다.
K시까지 진행하는 회의를 선택한 case 1과 K`시까지 진행하는 회의를 선택한 case 2가 있다면, case 2에서 선택할 수 있는 나머지 경우의 수는 case 1에서도 반드시 선택할 수 있다.
따라서 (1) 끝나는 시간이 빠른 회의부터 선택하고, (2) (끝나는 시간이 같다면) 빨리 시작하는 회의부터 선택함으로써 최대값을 구할 수 있다.
정리하면서 생각한 것
- 막대를 앞에서부터 채우고 싶으면 시작하는 시간을 기준으로 생각해야 할 것 같았는데, 끝나는 시간을 기준으로 생각해야 하는구만
- 이 문제에서는 0시~24시 같은 상식이 통하지 않으니까 (시간의 최댓값은 2^31-1) 그냥 마구마구 비교해 주면 된다. 끝나는 시간이 빠르다는 건 시작하는 시간도 빠르다는 뜻임 (시작하는 시간 <= 끝나는 시간)
- 그리디 알고리즘은 어떤 순간에 최적이라고 생각되는 해가 최종적으로 최적이 되는 상황에 쓴다.
앞에서부터 시간표를 채워 나가면서 여백의 시간표를 가장 많이 남겨둘 수 있는 선택지를 그때그때 선택하는 식으로 이해하면 될 것 같다.- 근데 이러면 회의가 늦게 시작하는 순으로 선택하면서 나아가도 되는 거 아닌가?

챗지한테 물어보니까 이런 대답을 하는데... 잘 이해가 안된다. 근데 실제로 뚜드려 보면 시작하는 시간이 늦은 순서로 풀었을 땐 틀린 답이 나옴. 학교 가서 고인물들을 괴롭혀 봐야겠다...
- 근데 이러면 회의가 늦게 시작하는 순으로 선택하면서 나아가도 되는 거 아닌가?
