본인이 공부하기 위한 목적의 글 입니다.

Abstract

복잡한 RNN or CNN 기반의 dominant 시퀀스 변환 모델들이 인코더와 디코더를 포함하고, 가장 성능이 좋은 모델들은 인코더와 디코더를 어텐션 메커니즘을 통해 연결하는 것을 보여주었다.

저자들은 완전히 재귀적인 처리와 합성곱을 배제하고 어텐션 메커니즘만을 기반으로 하는 새로운 단간한(?) 네트워크 아키텍처인 Transformer를 제안한다.

두 가지 기계 번역 작업세어의 실험 결과는 이 모델이 훨씬 더 병렬화가 가능하며 훈련에 걸리는 시간도 매우 적고 동시에 품질도 더 우수하다는 것을 보여준다.
저자들은 Transformer가 대규모 및 제한된 훈련 데이터를 사용하여 영어 구문 분석에도 성공적으로 적용됨을 보여줌으로써 이 모델이 다른 작업에 대해서도 잘 일반화된다는 것을 입증하였다.

서론

CNN, 특히 LSTM과 게이트된 RNN은 시퀀스 모델링에서 최점단 기술로 확립되어 왔다.
이 논문의 저자들은 RNN 대신 Self-Attention을 사용하여 Transformer 모델을 설계하였다.

순환 모델은 일반적으로 입력과 출력 시퀀스의 심볼 위치를 따라 계산을 분해한다.
계산 시간 단계에 위치를 맞추어, 이전 숨겨진 상태

와 t 위치의 입력을 함수로 사용하여 숨겨진 상태

시퀀스를 생성한다.
이러한 본질적으로 순차적인 특성으로 인해 훈련 예제 내에서 병렬화가 불가능하며, 긴 시퀀스 길이에서는 메모리 제한으로 인해 예제 간 배치가 제한됩니다.

어텐션 메커니즘은 입력 또는 출력 시퀀스에서의 거리에 관계없이 종속성을 모델링하여 다양한 작업에서 매력적인 시퀀스 모델링 및 변환 모델링의 필수 구성 요소가 되었다.
그러나 이러한 어텐션 메커니즘은 몇 가지 예외를 제외하고는 순환 네트워크와 함께 사용된다.

본 논문에서는 순환을 배제하고 어텐션 메커니즘만을 사용하여 입력과 출력 간의 전역 종속성을 그리는 모델 아키텍처인 Transformer를 제안한다.
Transformer는 훨씬 더 많은 병렬화가 가능하며, 8개의 P100 GPU에서 12시간만 훈련하더라도 번역 품질의 새로운 최첨단 기술에 도달할 수 있다.

Background

Self-attention은 시퀀스의 여러 위치를 관련시켜 시퀀스의 표현을 계산하는 어텐션 메커니즘이다.
Self-attention은 읽기 이해, 추상적 요약, 텍스트 기술 및 태스크 독립적인 문장 표현 학습 등 다양한 작업에서 성공적으로 사용되었다.
End-to-end 메모리 네트워크는 순차적 계산 대신 재귀적인 어텐션 메커니즘을 기반으로 하며 간단한 언어 질문 응답 및 언어 모델링 작업에서 잘 수행되었다.

모델 아키텍처

경쟁력 있는 대부분의 신경망 시퀀스 변환 모델은 인코더-디코더 구조를 가지며, 인코더는 심볼 표현의 입력 시퀀스(x1, ..., xn)를 연속적인 표현 z = (z1, ..., zn)의 시퀀스로 매핑하고, 디코더는 z를 입력으로 받아 기호 출력 시퀀스(y1, ..., ym)를 한 번에 하나씩 생성한다.

모델은 자기 회귀적이며, 다음을 생성할 때 이전에 생성된 기호를 추가 입력으로 사용한다.

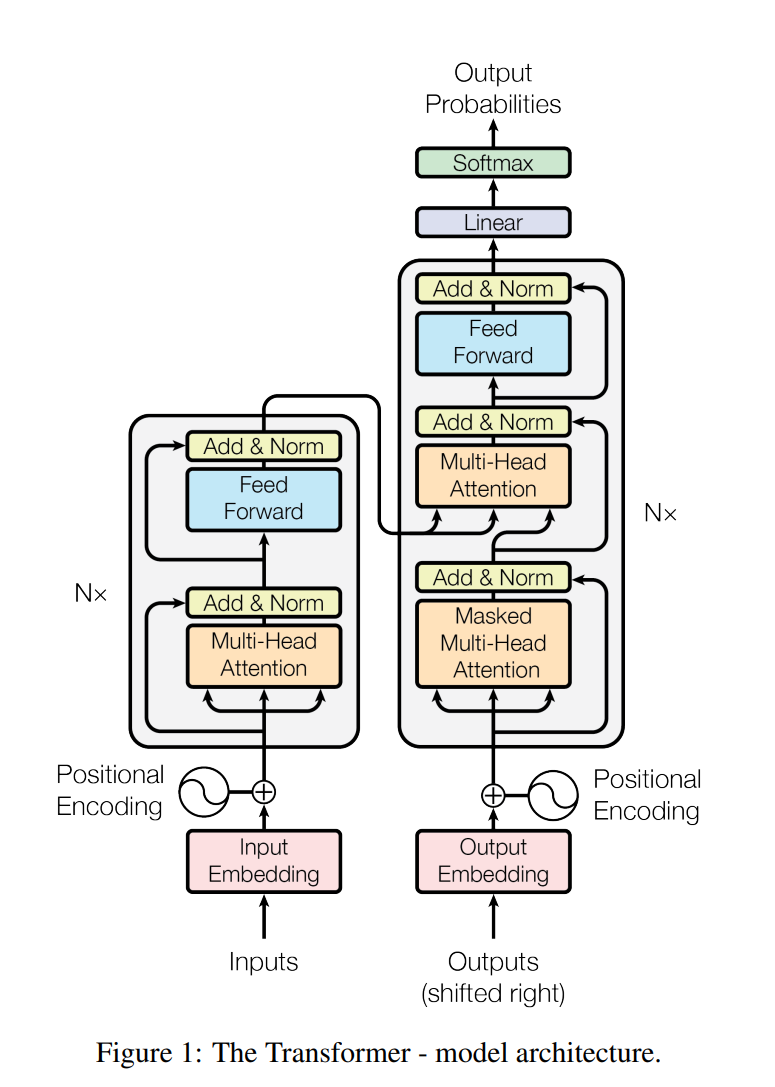
Transformer는 이러한 전체적인 아키텍처를 따르며, 인코더와 디코더 모두에 대해 적층된 self-attention 및 포인트-와이즈, 완전히 연결된 레이어를 사용합니다.

이는 그림 1의 왼쪽과 오른쪽 반에 나타나 있다.

인코더와 디코더의 스택

인코더(그림 왼쪽)

인코더는 N = 6개의 동일한 레이어로 구성된다. 각 레이어는 두 개의 서브레이어로 이루어져 있다.
첫 번째는 멀티 헤드 self-attention 메커니즘이고, 두 번째는 간단한 position-wise 완전히 연결된 피드 포워드 네트워크이다.
각각의 서브레이어 주위에는 잔차 연결(residual connection)과 레이어 정규화가 적용된다.
즉, 각 서브레이어의 출력은 LayerNorm(x + Sublayer(x))이다.
여기서 Sublayer(x)는 서브레이어가 구현한 함수다.
이러한 잔차 연결을 용이하게 하기 위해 모델의 모든 서브레이어 및 임베딩 레이어는 dmodel = 512 차원의 출력을 생성합니다.

디코더

디코더도 N = 6개의 동일한 레이어로 구성된다.
각 인코더 레이어에 두 개의 서브레이어가 있을 뿐만 아니라, 디코더는 인코더 스택의 출력에 대한 멀티 헤드 어텐션을 수행하는 세 번째 서브레이어를 추가한다.
인코더와 마찬가지로 각 서브레이어 주위에는 잔차 연결이 적용되고, 이어서 레이어 정규화가 이루어진다.
또한 디코더 스택에서 self-attention 서브레이어를 수정하여 위치가 이후 위치를 참조하지 못하도록 막는다.
이러한 마스킹은 출력 임베딩이 하나의 위치만큼 offset되므로, 위치 i의 예측은 i보다 작은 위치의 알려진 출력에만 의존할 수 있도록 보장한다.

Attention

어텐션 함수는 쿼리(query)와 키-값(key-value) 쌍 세트를 출력(output)으로 매핑하는 함수로서, 여기서 쿼리, 키, 값 및 출력은 모두 벡터이다.
출력은 값(value)들의 가중 합으로 계산되며, 각 값에 할당된 가중치는 쿼리와 해당 키(key)의 호환성 함수에 의해 계산된다.

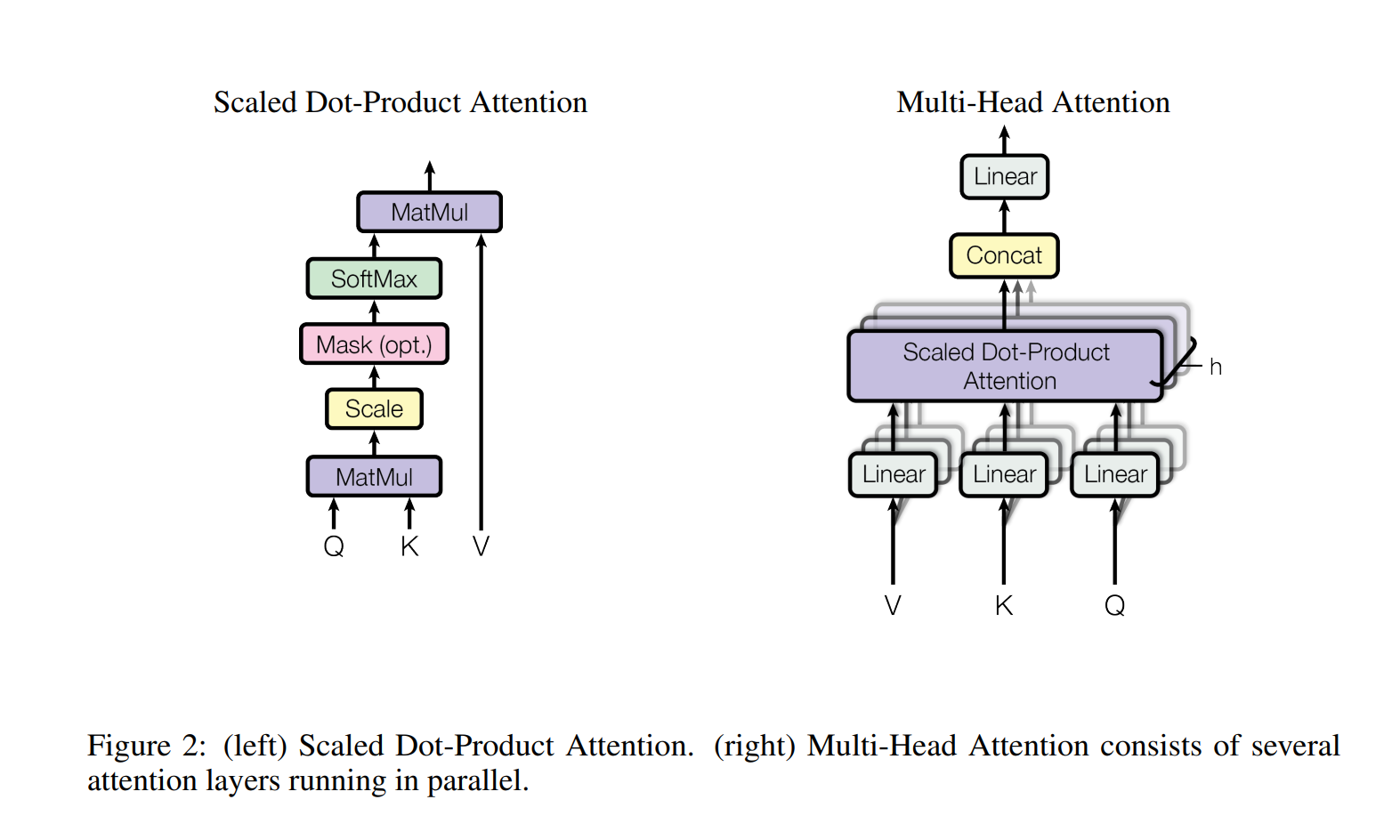
Scaled Dot-Product Attention

우리는 어텐션 함수를 "Scaled Dot-Product Attention"이라고 부른다.
입력은 각각 차원이

인 쿼리(query)와 키(key) 그리고 차원이

인 값(value)으로 이루어져 있다.
우리는 쿼리와 모든 키(key) 간의 점곱(dot product)을 계산하고,

로 나눈 다음 softmax 함수를 적용하여 값을 가중치로 변환한다.

실제로는, 우리는 쿼리들을 행렬 Q로 묶어 한 번에 어텐션 함수를 계산한다.
키(key)와 값(value)도 행렬 K와 V로 묶어 계산한다.
출력의 행렬은 다음과 같이 계산된다.

가장 일반적으로 사용되는 어텐션 함수는 가산 어텐션과 도트 곱 어텐션이다.
도트 곱 어텐션은 우리의 알고리즘과 동일하지만

의 스케일링 요소가 다르다.
가산 어텐션은 단일 은닉층을 가진 피드 포워드 네트워크를 사용하여 호환성 홤수를 계산한다.
이 두가지 방법은 이론적 복잡성에서는 유사하지만, 도트 곱 어텐션은 고도로 최적화된 행렬 곱셈 코드를 사용하여 훨씬 더 빠르고 공간 효율적이다.

의 작은 값에 대해서는 두 가지 메커니즘이 유사하게 작동하지만,

의 값이 클수록 가산 어텐션은 도트 곱 어텐션보다 우수한 성능을 보인다.

의 값이 큰 경우 도트 곱이 매우 큰 크기를 가지므로, 소프트맥스 함수가 기울기가 매우 작은 영역으로 밀어넣을 가능성이 있다.
이러한 영향을 상쇄하기 위해 우리는 도트 곱의 값을

로 스케일링한다.

Multi-Head Attention

차원의 키(key), 값(value) 및 쿼리(query)를 사용하여 단일 어텐션 함수를 수행하는 대신, 논문의 저자들은 서로 다른 학습된 선형 투영을 사용하여 쿼리, 키 및 값 h번 선형 투영하여 각각 dk, dk 및 dv 차원으로 매핑하는 것이 유익하다는 것을 발견했다.

멀티 헤드 어텐션은 모델이 서로 다른 위치에서 서로 다른 표현 부분 공간(representation subspace)의 정보를 함께 어텐션 할 수 있도록 한다.
하나의 어텐션 헤드(head)만 사용하면, 평균화가 이를 방해한다.

Applications of Attention in our Model

Transformer는 멀티 헤드 어텐션을 세 가지 다른 방식으로 사용한다.

• "인코더-디코더 어텐션" 레이어에서 쿼리는 이전 디코더 레이어에서 가져오고, 메모리 키(key)와
  값(value)은 인코더 출력에서 가져온다.
  이를 통해 디코더의 모든 위치에서 입력 시퀀스의 모든 위치에 어텐션을 할 수 있다.
  이것은 [38, 2, 9]와 같은 seq2seq 모델의 전형적인 인코더-디코더 어텐션 메커니즘을 모방합니다.
• 인코더에는 self-attention 레이어가 있다.
  self-attention 레이어에서 모든 키(key), 값(value), 쿼리는 동일한 위치에서 가져온다.
  이 경우, 인코더의 이전 레이어 출력이다.
  인코더의 각 위치는 인코더 이전 레이어의 모든 위치에 어텐션을 할 수 있다.
• 마찬가지로, 디코더의 self-attention 레이어는 디코더의 각 위치가 해당 위치를 포함한 이전 디코더의 모든 위치에 어텐션 할 수 있도록 한다.
  자가 회귀 속성을 보존하려면 디코더에서 좌측 정보 흐름을 방지해야 한다.
  이를 위해 스케일드 닷-프로덕트 어텐션 내에서 softmax의 입력에서 잘못된 연결에 해당하는 모든 값을 마스킹(−∞로 설정)한다.

Position-wise Feed-Forward Networks

어텐션 서브 레이어에 추가로, 우리의 인코더와 디코더 각 레이어는 각 위치에 대해 독립적으로 적용되는 fully connected feed-forward 네트워크를 포함한다.
이것은 ReLU 활성화 함수를 거친 두 개의 선형 변환으로 구성된다.

선형 변환은 서로 다른 위치에서 동일하지만, 레이어 간에는 다른 파라미터를 사용한다.
이를 다른 방법으로 설명하면 커널 크기가 1인 두 개의 컨볼루션(convolution)으로 볼 수 있다.
입력과 출력의 차원은 d{model} = 512이며, 내부 레이어는 d{f f} = 2048의 차원을 가진다.

Embeddings and Softmax

다른 시퀀스 전이 모델과 마찬가지로, 입력 토큰과 출력 토큰을 d_{model} 차원의 벡터로 변환하기 위해 학습된 임베딩을 사용한다.
또한 디코더 출력을 예측된 다음 토큰 확률로 변환하기 위해 보통의 학습된 선형 변환과 소프트맥스 함수를 사용한다.
우리 모델에서는 두 임베딩 레이어와 프리-소프트맥스 선형 변환 사이에서 동일한 가중치 행렬을 공유하며, 이는 [30]과 유사합니다.
임베딩 레이어에서는 이러한 가중치를

로 곱한다.

Positional Encoding

Transformer 모델은 순환 및 합성곱을 포함하지 않으므로 시퀀스의 순서를 활용하기 위해 상대적이거나 절대적인 위치에 대한 정보를 주입해야한다.
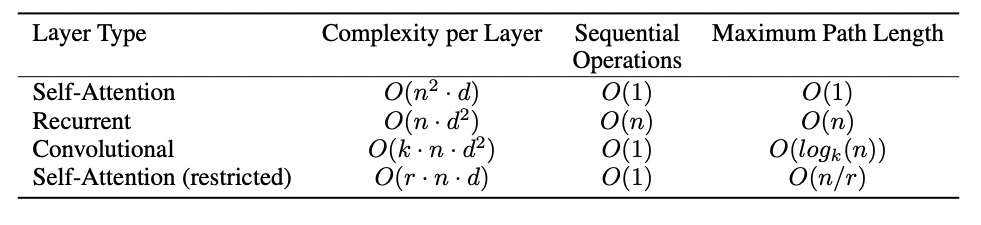
테이블 1은 다양한 레이어 유형에 대한 최대 경로 길이, 각 레이어의 복잡성 및 최소 순차 작업 수를 보여준다.
여기서 n은 시퀀스의 길이이고, d는 표현 차원이다.
합성곱의 커널 크기는 k이며, 제한된 self-Attention 에서의 이웃의 크기는 r입니다.

모델이 순서를 고려하려면, 임베딩을 통해 입력 순서의 상대적인 또는 절대적인 위치에 대한 정보를 추가해야 한다.
이를 위해, 우리는 인코더와 디코더 스택의 맨 아래쪽에 "위치 인코딩"을 추가한다.
위치 인코딩은 임베딩과 동일한 d_{model} 차원을 가지고 있으므로 두 값을 더할 수 있다.
위치 인코딩에는 학습 가능한 것과 고정된 것이 여러 가지 선택지가 있다.

본 연구에서는 다른 주파수의 사인 및 코사인 함수를 사용합니다:

이 작업에서는 다음과 같은 사인 및 코사인 함수를 사용합니다.

pos, i는 각각 위치와 차원을 나타낸다.
즉, 위치 인코딩의 각 차원은 사인파에 해당한다.
파장은 2π에서 10000·2π까지의 기하급수적 진행으로 형성된다.
이 함수를 선택한 이유는 상대적 위치에 대해 쉽게 학습할 수 있도록 모델이 참조를 수행하게 할 것이라고 가정했기 때문이다.
즉, 고정된 k 오프셋에 대해 P E{pos+k}는 P E{pos}의 선형 함수로 표현될 수 있다.
또한 학습된 위치 임베딩을 사용하기도 했지만, 두 버전이 거의 동일한 결과를 내놓았기 때문에 (표 3의 E 행 참조) 사인 함수 버전을 선택했다.
사인 함수 버전은 훈련 중 경험한 시퀀스 길이보다 더 긴 시퀀스 길이로 추정하는 것이 가능하기 때문이다.

Why Self-Attention

이 섹션에서는 심볼 표현 (x1, ..., xn)으로 이루어진 변수 길이의 하나의 시퀀스를 같은 길이의 다른 시퀀스 (z1, ..., zn)로 매핑하는 일반적인 시퀀스 변환 인코더 또는 디코더의 히든 레이어와 같이 사용되는 재귀 및 합성곱 레이어와 self-attention 레이어의 다양한 측면을 비교한다.
Self-attention을 사용하는 동기는 세 가지이다.

1. 첫 번째는 각 레이어당 총 계산 복잡성이다.
2. 두 번째는 순차적으로 실행되어야 하는 최소 연산 수에 따라 측정된 것처럼 병렬화할 수 있는 계산 양이다.
3. 세 번째는 네트워크 내에서 장거리 종속성 간 경로 길이이다.

장거리 종속성을 학습하는 것은 많은 시퀀스 변환 작업에서 핵심적인 과제 중 하나이다.
이러한 종속성을 학습하는 능력에 영향을 미치는 주요 요인 중 하나는 신호가 네트워크 내에서 이동해야 하는 순방향 및 역방향 경로의 길이이다.
입력 및 출력 시퀀스의 모든 위치 조합 간의 최대 경로 길이를 비교하여 다른 레이어 유형으로 구성된 네트워크의 두 지점 간 최대 경로 길이를 비교한다.

위의 표에서 볼 수 있듯이, self-attention layer는 일련의 실행 작업에서 모든 위치를 연결하지만, 순환 레이어는 O(n) 시간 순차적인 작업이 필요하다.
계산 복잡도 측면에서, self-attention layer는 대부분의 경우 기계 번역에서 사용되는 문장 표현에 대해 사용되는 word-piece 및 byte-pair 표현과 같이 시퀀스 길이 n이 표현 차원 d보다 작을 때, 순환 레이어보다 빠르다.
매우 긴 시퀀스를 사용하는 작업의 경우, self-attention은 해당 출력 위치를 중심으로 입력 시퀀스의 크기 r의 이웃만 고려하도록 제한함으로써 계산 성능을 향상시킬 수 있다.
이렇게 하면 최대 경로 길이가 O(n/r)로 증가한다.

커널 너비 k < n인 단일 컨볼루션 레이어는 모든 입력 및 출력 위치 쌍을 연결하지 않는다.
연속적인 커널의 경우, O(n/k)개의 컨볼루션 레이어가 필요하며, 확장 컨볼루션의 경우 O(logk(n))이 필요하다.
이는 네트워크 내의 어떤 두 위치 사이의 가장 긴 경로의 길이를 증가시킨다.
컨볼루션 레이어는 일반적으로 재귀 레이어보다 계산 비용이 더 많이 든다.
하지만 분리 가능한 컨볼루션은 계산 복잡도를 크게 줄이며, O(k · n · d + n · d2)의 계산 복잡도를 가진다.
그러나 k = n인 경우라도 분리 가능한 컨볼루션의 복잡도는 우리 모델에서 취하는 self-attention 레이어와 point-wise feed-forward 레이어의 조합과 동일하다.
부수적인 이점으로, self-attention은 더 해석 가능한 모델을 제공할 수 있다.
Transformer 모델에서 attention 분포를 조사하고 그 예시를 제시하고 논의한다.
개별 attention head는 명확히 다른 작업을 수행하는 것으로 나타나며, 많은 attention head는 문장의 문법 및 의미 구조와 관련된 동작을 나타내는 것으로 나타났다.

Training

이 섹션은 모델의 학습 과정을 설명한다.

Training Data and Batching

이 섹션에서는 우리 모델의 훈련 방법에 대해 설명한다.

대략 4.5백만 개의 문장 쌍으로 구성된 표준 WMT 2014 영어-독일어 데이터셋을 사용하여 훈련 했다.
문장은 바이트 페어 인코딩을 사용하여 인코딩되었으며, 공유 소스-타겟 어휘는 약 37,000개의 토큰으로 구성되었다.
영어-프랑스어의 경우, 약 3600만 개의 문장으로 구성된 WMT 2014 영어-프랑스어 데이터셋을 사용했으며, 토큰을 32000 개의 워드 피스로 분할했다.
문장 쌍은 대략적인 시퀀스 길이에 따라 배치되었다.
각 훈련 배치는 대략 25,000개의 소스 토큰과 25000개의 타겟 토큰을 포함하는 문장 쌍의 집합을 포함했다.

Hardware and Schedule

우리는 8개의 NVIDIA P100 GPU가 장착된 한 대의 컴퓨터에서 모델을 훈련했다.
논문 전체를 통해 설명된 하이퍼파라미터를 사용한 기본 모델의 경우, 각 훈련 단계는 약 0.4초가 걸렸다.
우리는 기본 모델을 총 10만 단계 또는 12시간 동안 훈련시켰다.
대형 모델의 경우(표 3의 마지막 줄에 설명되어 있음), 각 단계 시간은 1.0초였다.
대형 모델은 30만 단계(3.5일) 동안 훈련되었다.

Optimizer

학습에 Adam optimizer를 사용했으며, 하이퍼파라미터는 β1=0.9, β2=0.98, ε=10^(-9)로 설정했다.
학습 중에는 다음 공식을 사용하여 학습률을 조정했다.

이는 처음 warmup_steps 회 학습시키면서 선형적으로 학습률을 증가시키고, 그 이후로는 단계 번호의 역제곱에 비례하여 학습률을 감소시키는 공식에 따라 학습률을 변화시키는 것과 일치하다. warmup_steps 값으로는 4000을 사용했다.

Regularization

학습 중에 세 가지 유형의 정규화를 사용한다.

1. Residual Dropout

2. BLEU

3. Label Smoothing