DFS vs BFS 탐색

코딩테스트에 통과하려면 무조건 풀어야 하는 문제유형은 DFS,BFS인것 같다😂😂😂
그래서 참 많은 유튜브와 블로그의 글들을 보고 개념은 이해했지만,
문제에 적용해서 코딩하는거까지는 쉽지않은과정이라고 생각한다.
(개인적으로 해당 유튜브가 개념을 이해하는데 가장 쉬움 -> 유튜브 링크)

그래서 일단 차근차근 개념부터 제대로 이해해보자!
우선 DFS와 BFS를 이해하기전에 간단하게 그래프를 알아야한다.

그래프(Graph)

정점과 간선으로 이루어진 자료구조

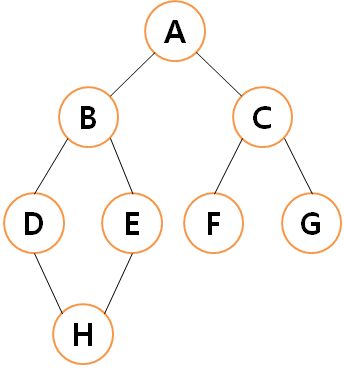
그래프 탐색이란?

하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한번씩 방문하는 것이다.
곧 DFS와 BFS는 그래프탐색의 일종이다.

DFS(Depth-First Search) 깊이 우선 탐색

DFS란?

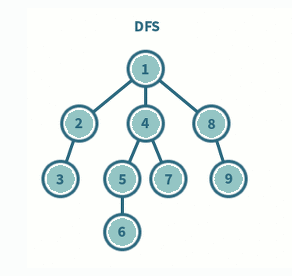
• 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법 (자식들을 우선적으로 탐색하는 방법)
• 스택 또는 재귀함수로 구현
• 한 노드에서 제일 마지막 자식까지 탐색하고 돌아오는 과정을 '백트리킹(Backtracking)'
• ⚠방문한 노드는 확실하게 확인해줘야한다. 그렇치 않으면 무한루프에 빠지게 된다.

BFS(Breadth-First Search) 너비 우선 탐색

BFS란?

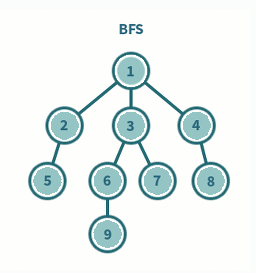
• 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드부터 방문하는 방법
• 큐를 이용하여 구현
• 최단거리를 구하는 문제에서 자주 사용된다.

---

DFS vs BFS 비교

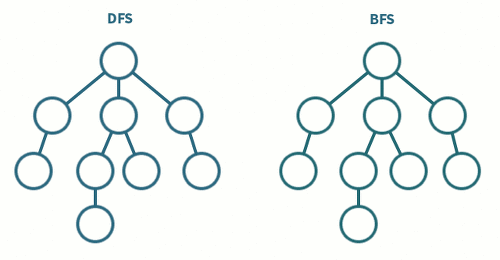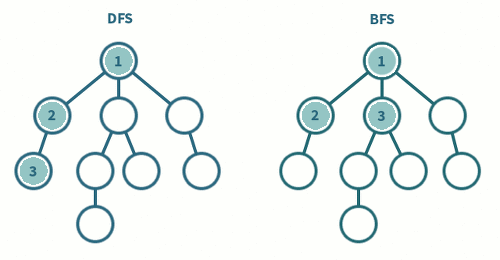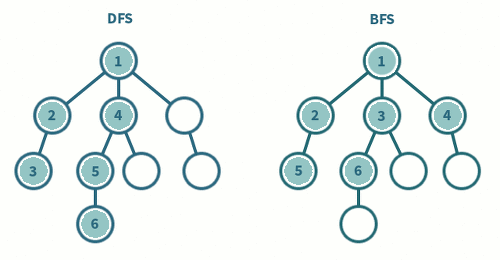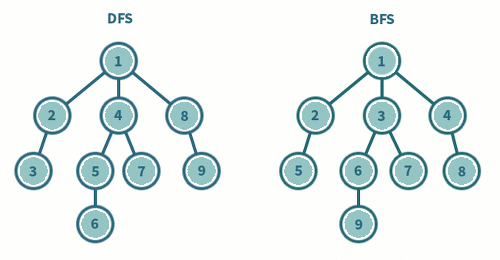
1. 속도 : DFS < BFS (여기서 표현하는 부등호는 크기가 아니라 더 좋은쪽을 표시)

• 속도면에서는 DFS보다 BFS가 훨씬 빠르다. 왜냐하면, DFS같은 경우 모든 노드를 방문하기 때문이다.
  
  

2. 구현방법

• DFS : 스택이나 재귀함수(인접행렬)로 구현
• BFS : 큐를 이용하여 구현

3. DFS와 BFS 선택방법은???

• DFS : 이동한 정점의 값을 가지고 계속 연산을 하는 경우(재귀적으로 호출되는경우)
• BFS : 최단거리 문제

ex1) 지구 상에 존재하는 모든 친구 관계를 그래프로 표현한 후 Ash 와 Vanessa 사이에 존재하는 경로를 찾는 경우

• DFS - 모든 친구 관계를 다 살펴봐야할지도 모름
• BFS - Ash와 가까운 관계부터 탐색
  
  

💡 이제 개념을 알았으니 코딩으로 DFS와 BFS를 이해해보자!

DFS vs BFS 문제로 이해하기

문제예제는 기본적인 코딩을 공부하기위해 백준 126번 문제 DFS와 BFS로 선택했다.

DFS, BFS탐색순으로 결과를 출력하면 된다.

문제 예시

// 입력1      
4 5 1
1 2
1 3
1 4
2 4
3 4
// 출력1 
3 1 2 5 4 (DFS)
3 1 4 2 5 (BFS)

문제 접근

1. 시작정점을 시작으로 map[][]==1인 경우이면서, 아직 방문하지 않은 경우(visited[]==false)
2. • (DFS) 1번을 만족하는 경우 break문으로 빠져나온다.
   • (BFS) 1번을 만족하면, for안에서 끝까지 탐색한다.

DFS의 경우 , 인접행렬, 인접리스트 , 스택 총 3가지 방법을 이용해 구현해보았다.

1. 인접행렬 : 정점의 개수가 적은 경우에만 사용하는 것을 권장한다. 왜냐하면, 정점n개에 대해 행렬의 크기가 n*n만큼 차지하기 때문에 n의 수가 시간복잡도 O(n^2)가 된다.
2. 인접리스트 : 모든 정점을 탐색하는 최악의 경우를 제외한 나머지 경우 인접행렬보다는 빠른 시간복잡도인 O(n+E)이다. (E는 간선의 개수)
3. 스택 : 1,2번과 달리 재귀호출을 하지 않는 방식으로 구현가능하다.

BFS는 큐를 이용하여 구현해보았다.

소스코드

static int map[][];		    // 정점과 간선을 표현하는 행렬
                                    // 입력1로 예를 들면 map[1][2] == 1
                                    // 사이즈는 n+1로 지정 
static ArrayList<TreeMap<Integer, Integer>> arrayList;	// 인접리스트 표현
static LinkedList<Integer>[] adjList;			// 인접리스트 표현(LinkedList([]))
static boolean[] visited;		
static int n,m,v;			// 정점의 개수, 간선의 개수, 시작 정점
static String answer = "";
    
// 인접행렬로 구현한 DFS (정점의 개수가 작은 경우에만 사용하는걸 권장)
public static void dfs_adjacency_matrix(int v) {
	visited[v] = true;
	answer += v+" ";
	System.out.println(answer);
	for(int i=1;i<m;i++) {
		if(map[v][i] == 1 && !visited[i]) {
			dfs_adjacency_matrix(i);
		}
	}
}

// 인접리스트로 구현한 DFS
public static void dfs_adjacency_list(int v) {
	visited[v] = true;
	answer += v+" ";
	
	TreeMap<Integer, Integer> tmap = arrayList.get(v);
	for(int i : tmap.keySet()) {
		if(!visited[i]) {
			dfs_adjacency_list(i);
		}
	}
	
}

// 스택으로 구현한 DFS
public static void dfs_stack(int v) {
	Stack<Integer> stack = new Stack<Integer>();
	stack.push(v);
	
	while(!stack.isEmpty()) {
		int vv= stack.pop();
		visited[vv] = true;	
		answer += vv+" ";
		
		for(int i=1; i<n+1;i++) {
			if(map[vv][i] == 1 && !visited[i]) {
				stack.push(i);			// stack에 담고 빠져나온다.
				break;
			}
		}
	}
	
}

// 큐로 구현한 BFS (인접행렬)
public static void bfs_queue_adjacency_matrix(int v) {
	Queue<Integer> q = new LinkedList<Integer>();
	q.offer(v);
	visited[v] = true;
	
	while(!q.isEmpty()) {
		int vv = q.poll();
		answer += vv+" ";
		
		for(int i=1; i<n+1 ; i++) {
			if(map[vv][i] == 1 && !visited[i]) {
				q.offer(i);			// queu에 담고 계속 진행 map[vv][i~n] 끝까지 탐색
				visited[i] = true;
			}
		}
	}
}

// 큐로 구현하는 BFS (인접리스트)
public static void bfs_queue_adjacency_list(int v){
	Queue<Integer> q = new LinkedList<Integer>();
	visited[v] = true;
	q.add(v);

	while(!q.isEmpty()){
		v = q.poll();
		answer += v +" ";
		
		Iterator<Integer> it = adjList[v].listIterator();
		while(it.hasNext()){
			int w = it.next();
			if(!visited[w]){
				visited[w]=true;
				q.add(w);
			}
		}
	}
}

전체 소스보기

dfs를 스택으로 구현하는 방식과 bfs를 큐로 구현한 소스를 비교해보니 사실 큰 차이점은 없었다.🙄🙄🙄.....?? 당연히 그래프탐색에서 방향성만 다른거니까,,,,당연한거지만😂 그래서 정리를 해보자면

for문을 돌면서 탐색해야하는 정점이면서 방문하지 않은 경우,
break으로 빠져나오면 DFS, 그렇지 않고 계속해서 정점을 탐색한다면 BFS

---

[참조블로그]

그래프 이미지
DFS vs BFS gif
깊이 우선 탐색(DFS) 과 너비 우선 탐색(BFS)
DFS와 BFS - JAVA 정리 및 해설
BFS 너비 우선 탐색 - 인접리스트 / 인접행렬로 구현