Greedy Algorithm

chaming·2021년 1월 8일

알고리즘 개념알기

목록 보기

3/8

탐욕법(Greedy Algorithm)

순간의 최적의 해를 구해 결과를 도출하는 법

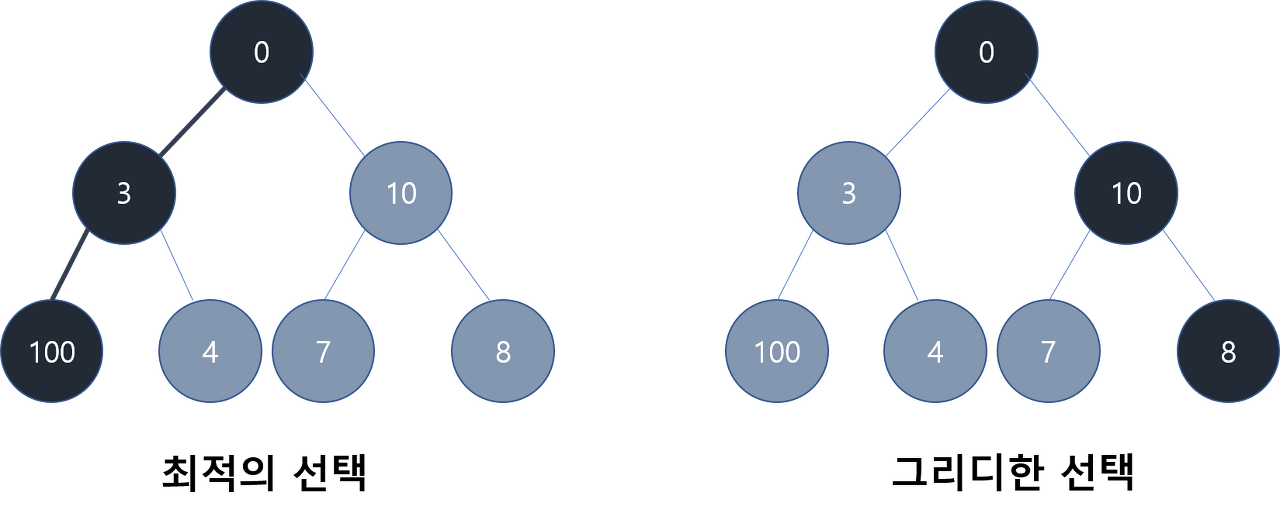
위의 그림에서 가장 큰값을 구하라하면, 정답은 100이다.
하지만, Greedy 알고리즘을 적용한다면 1depth에서 Max(3,10) = 10를 선택할것이고,_
2depth에서는 Max(7,8) = 8를 선택하여 최종 8라는 결과가 나온다.

위의 예제에서 알수 있듯, Greedy 알고리즘은 최적의 방법은 아니다!🙅‍♀️🙅‍♀️🙎‍♀️

✍단, 모든 노드를 탐색하지 않기 때문에 빠른 속도로 해를 구할수 있다는 장점을 가지고 있다.

탐욕법은 최적의해를 구하는 방법이 아니지만 코딩테스트에서 종종 출제되는 유형이다.
그렇다면 탐욕법을 이용하여 어떤 문제들을 접근하는게 좋은지 알아보자.

탐욕법은 언제 사용하면 좋을까?

활동선택문제
거스름돈 문제 (가장 대표적인 탐욕법 문제유형)
최소 신장문제
제약조건이 많은 대부분의 문제
다익스트라 알고리즘
... 등등 많은 문제

탐욕법 문제로 이해하기

문제는 해당 링크를 통해 확인가능하다.

HackerRank > Greedy >Candies

문제 제약조건

모두 1개의 캔디는 가져야한다.
나란히 앉은 경우, 옆의 학생의 점수가 더 높으면 캔디를 더 많이 줘야한다.

문제 예시

// 예제1 입력1 
int n = 8;
int[] arr = {2,4,3,5,2,6,4,5};
// 출력
long answer = 12

문제 접근

앞에서부터 뒤의 학생의 점수가 더 높으면 캔디를 더 많이줘야함.
그렇다면 맨뒤(n-1)의 학생인 경우, 바로 앞(n-2)학생보다 점수가 더 높으면, 캔디를 줌.

결론부터 이야기하자면, 이렇게 풀면 틀린다. 위의 예제1은 통과할 수 있다.

// 예제2 입력
int[] arr={ 1, 2, 3, 4, 5, 4, 3, 2, 1}

예제2와 같은 문제를 접근하기 위해서는
"앞에서 뒤로 비교, 그리고 뒤에서 앞으로 총 2번의 비교가 필요하다".

소스코드

public static long candies(int n, int[] arr) {
	long answer = n;

	int[] num = new int[n];
		
	// i는 0부터 n-1까지 , 다음수가 크면 num[i+1] =num[i]+1
	for(int i=0;i<n-1;i++){
		if(arr[i+1]>arr[i]){
			num[i+1] = num[i]+1;
		}
	}
		
	// i는 n-1부터 0까지, 이전수가 크면 num[i]+1와 num[i-1]중의 큰수를 선택
	for(int i=n-1;i>=1;i--) {
		if(arr[i] < arr[i-1]) {
			num[i-1] = Math.max(num[i]+1, num[i-1]);
		}
	}
	for(int i : num) {
	//	System.out.println(i);
		answer +=i;
	}
	System.out.println("answer : "+answer);
	return answer;
    }