Kruskal(크루스칼) 알고리즘

chaming·2021년 2월 3일

알고리즘 개념알기

목록 보기

7/8

크루스칼 알고리즘은 최소신종트리 알고리즘의 일종이다.
우선 신장트리가 무엇인지부터 알아보자!

🔊 신장트리(Spannig Tree)란?

그래프 중 모든 정점이 간선으로 연결되어 있고, 간선간의 사이클이 없는 그래프.

정점의 수 = 간선의 수 + 1

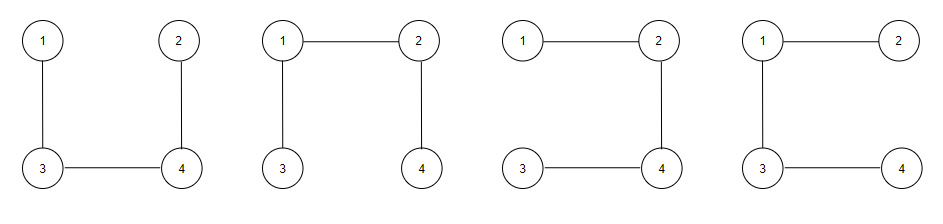
정점의 개수가 4개인 경우, 4개의 신장트리가 나온다.

최소신장트리(Minimum Spanning Tree) 알고리즘이란?

각 정점을 모두 연결하면서 가장 낮은 비용으로 연결된 신장트리
종류 : Kruskal , Prim 알고리즘

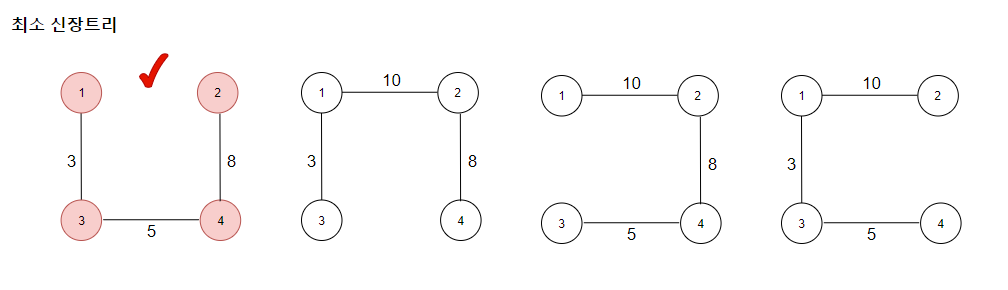
4개의 신장트리 중 비용이 가장 작은 첫번째 신장트리가 최소 신장트리가 된다.
MST알고리즘 중 크루스칼 알고리즘부터 공부해보자.

Kruskal(크루스칼) 알고리즘

Greedy 알고리즘의 일종으로 유니온 파인드 자료구조를 사용하는 알고리즘이다.
▶ 유니온 파인드 알고리즘 알아보기
해당 알고리즘은 간선을 기준으로 정점은 방문했는지 여부만 판단, '무방향 그래프'이다.

Kruskal 구현방법

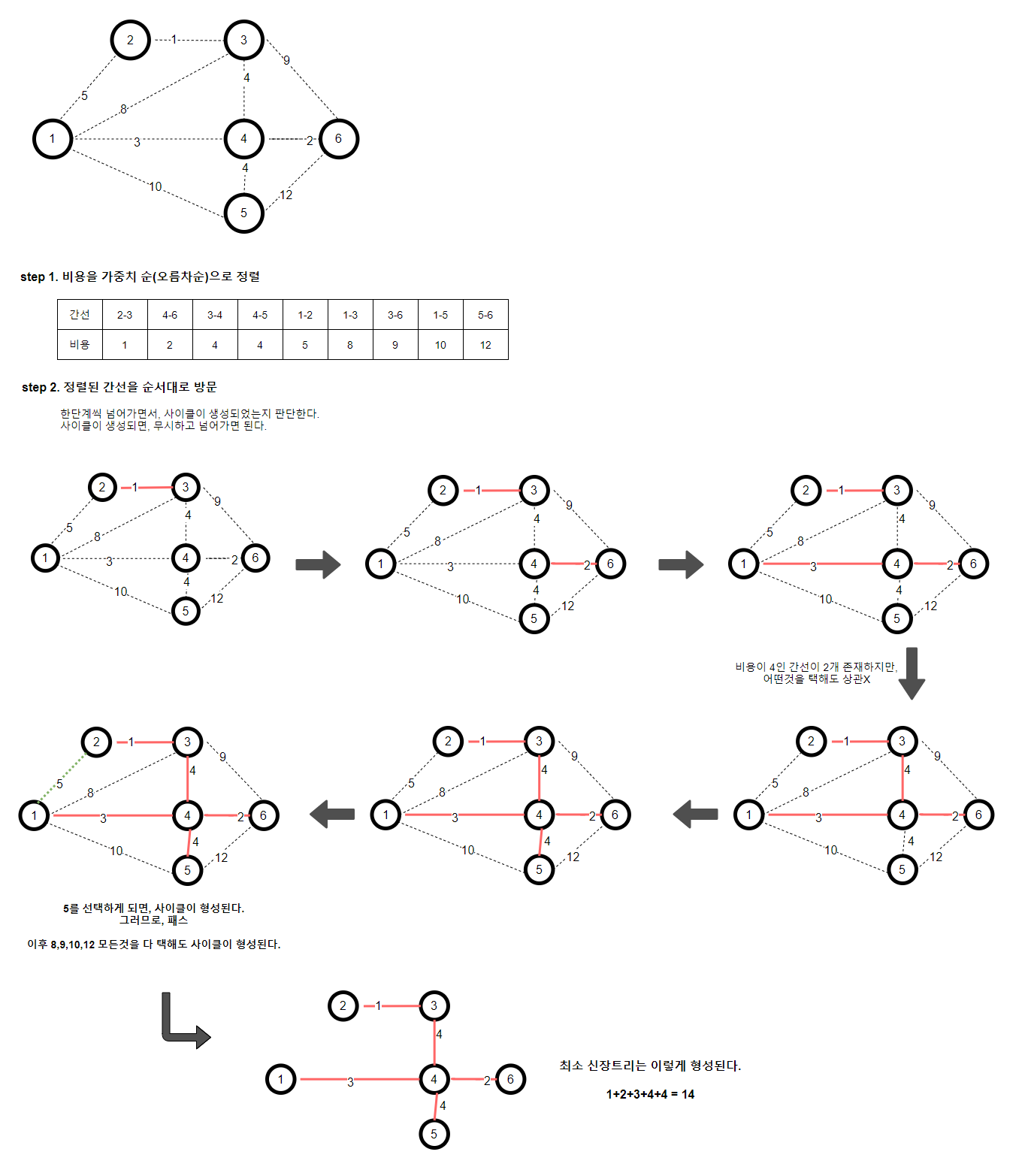
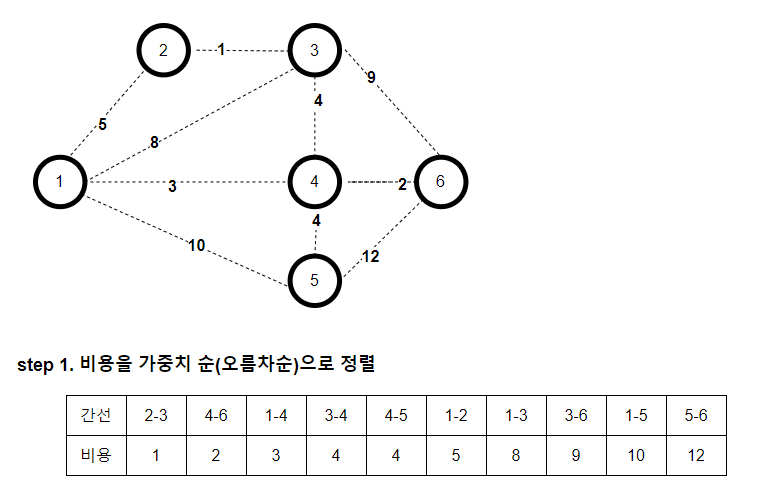각 정점을 잇는 간선들의 비용을 오름차순으로 정렬한다.
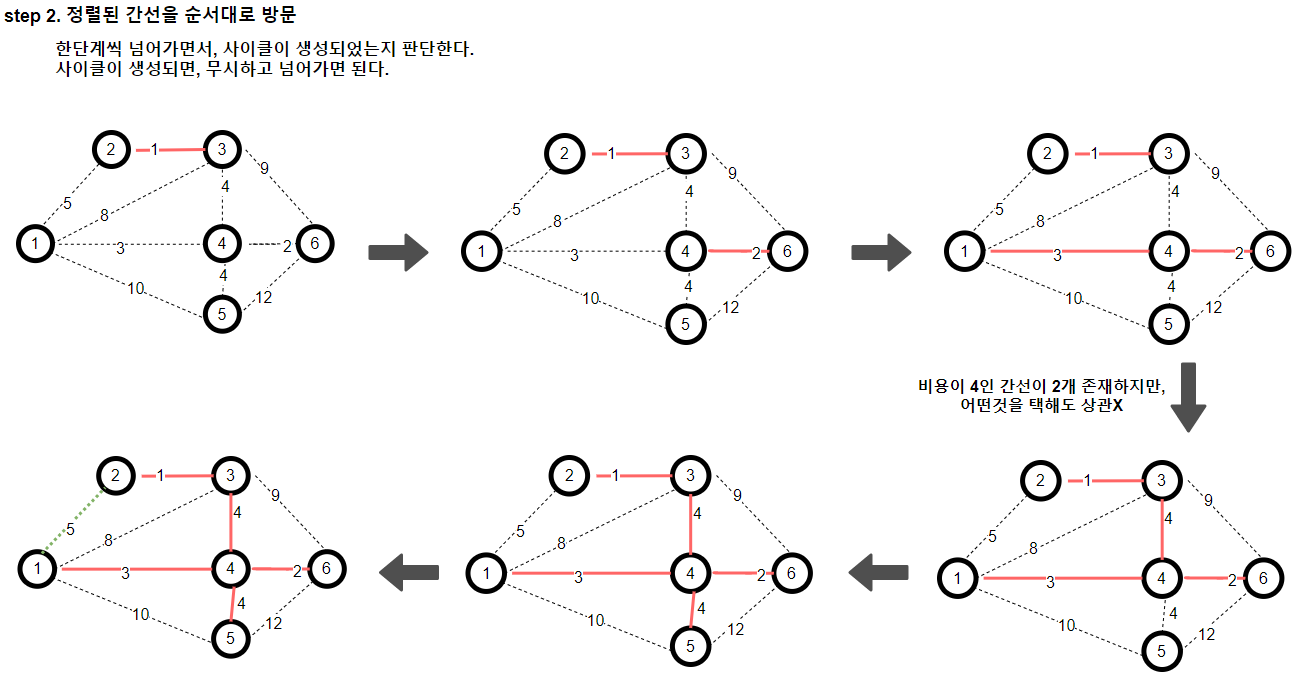순서대로 간선을 선택하면서 사이클이 생성되는지 여부를 확인한다.
❗ 5(초록색) 간선을 택하게 되는 경우 사이클이 발생한다.
이후 8,9,10,12 대한 간선 모두가 사이클이 형성되므로 패스한다.
그럼 최종적으로 MST는 아래와 같이 생긴다.

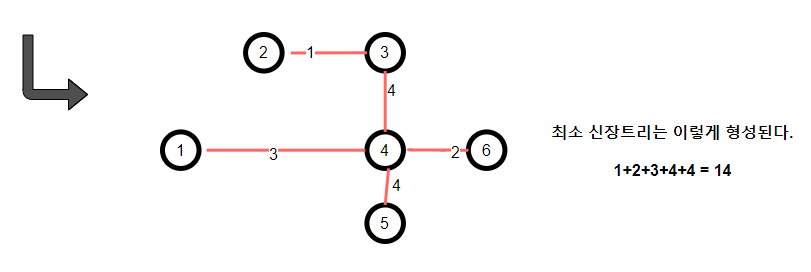
항상 그렇듯이 개념은 쉽게 이해가 된다.
이와 함께 부모노드값이 어떻게 변화하는지 다음단계에서 살펴보자.

Kruskal 간선 연결시 부모노드 변화

step0. 우선 부모노드가 자기 자신으로 설정한다.

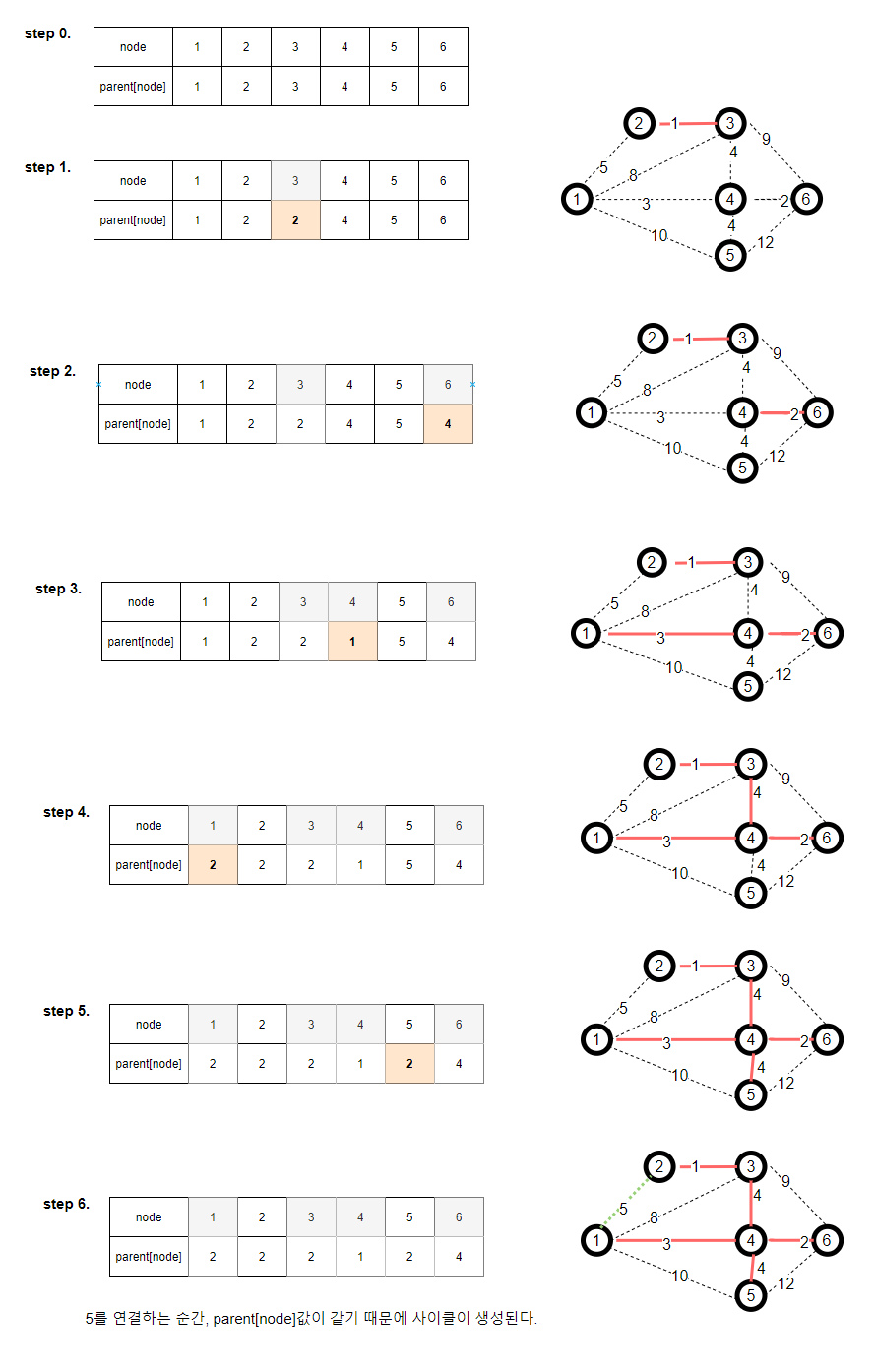
Kruskal 코드로 구현하기

간선에 대한 가중치를 정렬 후,
간선을 순서대로 선택하면서, 사이클이 형성되었는지 확인을 해야한다고 했다.
👉 이때 유니온 파인드 알고리즘을 이용하면 된다.

class Edge implements Comparable<Edge> {
    int n1;         // 정점1 (무방향 그래프라 시작, 종료 정점 구분 X)
    int n2;         // 정점2
    int cost;       // 비용

    Edge(int n1, int n2, int cost){
        this.n1 = n1;
        this.n2 = n2;
        this.cost = cost;
    }

    // 비용으로 오름차순 정렬하기 위한 Comparable method
    @Override
    public int compareTo(Edge edge) {
        return edge.cost >= this.cost ? -1 : 1;
    }
}

public class Kruskal {
    public static ArrayList<Edge> list = new ArrayList<Edge>();
    public static int[] parent;

    public static void main(String args[]){
        list.add(new Edge(1, 2, 5));
        list.add(new Edge(2, 3, 1));
        list.add(new Edge(3, 6, 9));
        list.add(new Edge(1, 4, 3));
        list.add(new Edge(1, 3, 8));
        list.add(new Edge(1, 5, 10));
        list.add(new Edge(4, 5, 4));
        list.add(new Edge(5, 6, 12));
        list.add(new Edge(4, 6, 2));
        list.add(new Edge(4, 3, 4));

        parent = new int[6+1];          // 1로 인덱스 맞추기 위함

        // 부모노드 자기 자신으로 초기화
        for(int i=1;i<parent.length;i++){
            parent[i] = i;
        }
	
    	// 비용을 오름차순으로 정렬
        Collections.sort(list);

        int sum = 0;
        for(int i=0;i<list.size();i++){
            Edge edge = list.get(i);
            // 사이클이 형성되어 있는지 체크
            if(!isConnect(edge.n1, edge.n2)){
                sum += edge.cost;               // 비용 +
                union(edge.n1, edge.n2);        // 간선 연결
            }
        }
    }
}