Prim(프림) 알고리즘

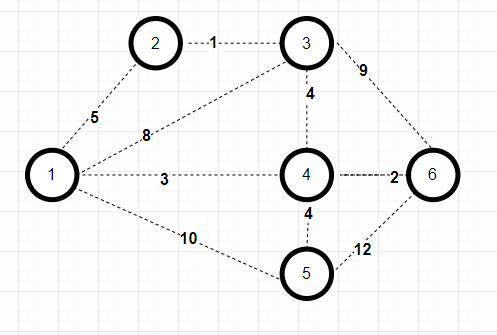
Prim 알고리즘 역시 MST 알고리즘의 일종이다.

Prim(프림) 알고리즘이란?

MST를 찾는 알고리즘. '무방향 그래프'
인접한 정점 중 최소비용으로 이동가능한 정점을 선택하면서 방문하는 알고리즘.
크루스칼 알고리즘과 같은 용도지만, 응용상황에 따라 두 알고리즘의 효율성이 달라질 수 있다.

🟢🟡🔴 Krusakl알고리즘과의 차이는 간선을 기준으로 하는것이 아닌 정점을 기준으로 판단하는 것이다.

Prim 알고리즘 그림으로 이해하기

앞서 Kruskal에서 이용했던 그래프를 그대로 이용해본다.


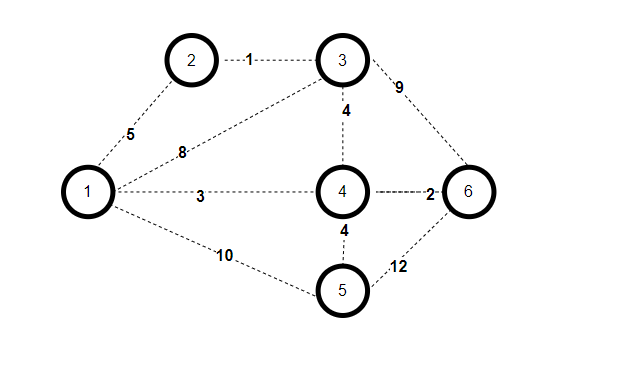
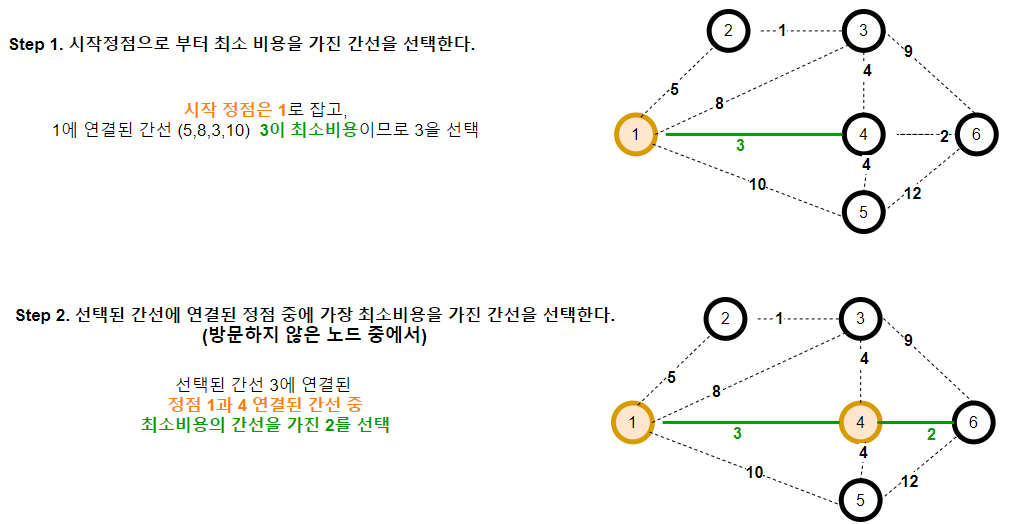
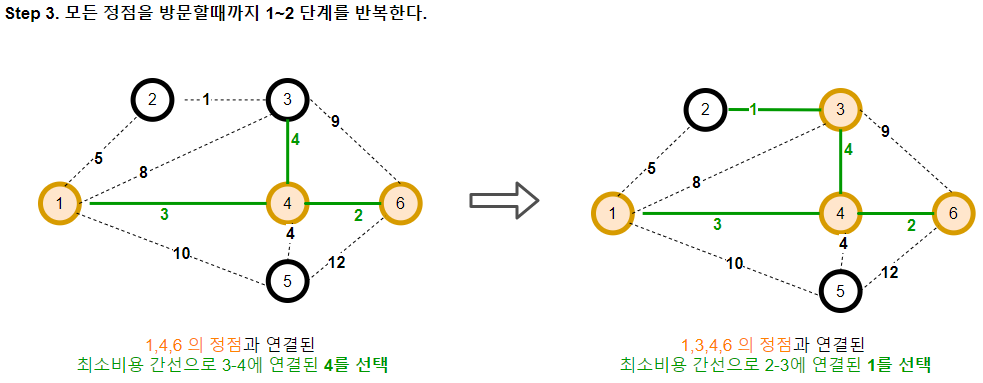
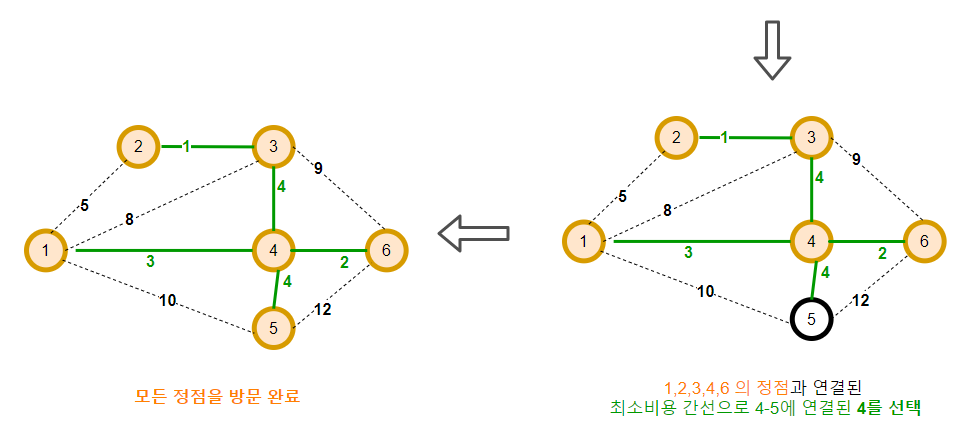
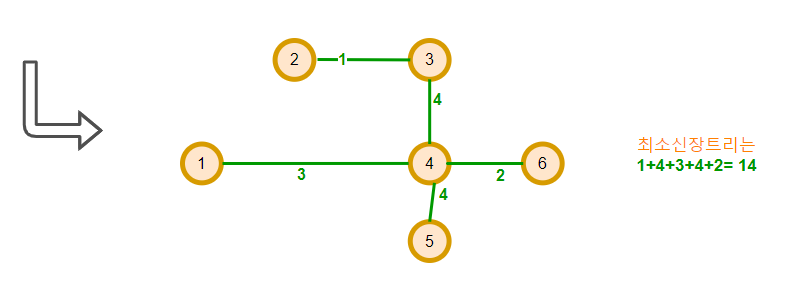
최종적으로 아래와 같은 MST가 완성된다.

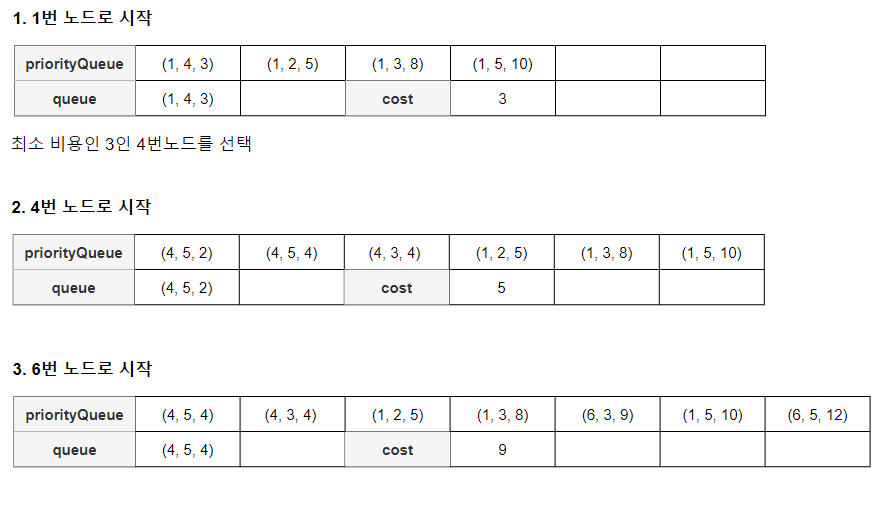
Prim 알고리즘 정점 선택시 Queue 변화

정점을 선택하는 경우 PriorityQueue, Queue의 변화를 살펴보자.
큐는 Node(start, end, cost)로 표현. (참고로 Queue는 한칸만 사용한다.)

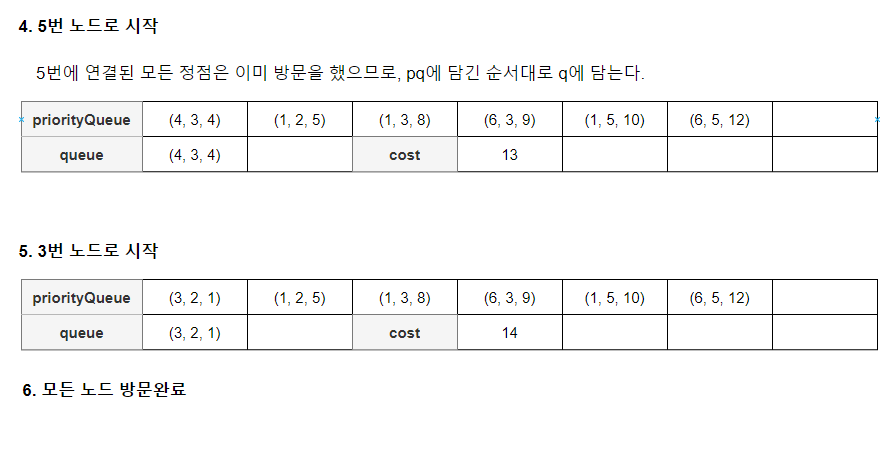
Prim 알고리즘 코드로 이해하기

연결리스트와 큐를 이용하여 구현한 Prim 알고리즘이다.
PriorityQueue는 비용을 오름차순으로 보기위해 사용.

public class Prim {

    public static ArrayList<Node> list = new ArrayList<Node>();
    public static ArrayList<Node>[] nodeList;                   // 연결리스트
    public static int costs = 0;
    public static boolean[] visited;

    public static void main(String args[]){
        // 그래프 설정 ( 정점, 간선 , 비용)
        list.add(new Node(1, 2, 5));
        list.add(new Node(2, 3, 1));
        list.add(new Node(3, 6, 9));
        list.add(new Node(1, 4, 3));
        list.add(new Node(1, 3, 8));
        list.add(new Node(1, 5, 10));
        list.add(new Node(4, 5, 4));
        list.add(new Node(5, 6, 12));
        list.add(new Node(4, 6, 2));
        list.add(new Node(3, 4, 4));

        visited = new boolean[6+1];          // 1로 인덱스 맞추기 위함
        Arrays.fill(visited, false);         // 방문여부 초기화

        nodeList = new ArrayList[6+1];
        for(int i=1;i<7;i++){     // 연결리스트 초기화
            nodeList[i] = new ArrayList<Node>();
        }

        // 연결리스트에 간선과 비용 설정
        for(int i=0;i<list.size();i++){
            int start = list.get(i).start;
            int end = list.get(i).end;
            int cost = list.get(i).cost;
            nodeList[start].add(new Node(start, end, cost));
            nodeList[end].add(new Node(end, start, cost));
        }

        mst_prim(1);        // 시작 정점 1
    }

    public static void mst_prim(int p){
        PriorityQueue<Node> pq = new PriorityQueue<Node>();     // 비용을 오름차순으로 정렬하는 Queue
        Queue<Integer> q = new LinkedList<>();

        // 시작노드
        q.offer(p);

        while(!q.isEmpty()){
            int node = q.poll();
            visited[node] = true;

            // node에 연결된 정점들에 대한 정보 중에서
            // 방문하지 않은 Node를 pq에 담는다.
            for(Node n : nodeList[node]){
                // 종료노드 
                if(!visited[n.end]){
                    pq.add(n);
                }
            }

            // pq에 담긴 정보들을 순차적으로 mst에 담는다.
            while(!pq.isEmpty()){
                Node e = pq.poll();

                if(!visited[e.end]){
                    q.add(e.end);
                    visited[e.end] = true;
                    costs += e.cost;                  
                    break;
                }
            }
        }
    }
}

class Node implements Comparable<Node>{
    int start;      // 시작 정점
    int end;        // 종료 정점
    int cost;       // 비용

    Node(int start, int end, int cost){
        this.start = start;
        this.end = end;
        this.cost = cost;
    }

    // 비용으로 오름차순 정렬하기 위한 Comparable method
    @Override
    public int compareTo(Node node) {
        return node.cost >= this.cost ? -1 : 1;
    }
}

전체 소스보기(git)

[참조]

#알고리즘_프림(Prim Algorithm) - Java
Prim 알고리즘 [프림][MST][JAVA]
최소 비용 신장 트리, 프림 알고리즘 JAVA로 구현하기