11-1. 탐색의 이해와 보간 탐색
탐색의 이해
탐색(Search)이란, 데이터를 찾는 방법이다.
앞에서 배운 '순차 탐색(linear search)'이나 '이진 탐색(binary search)'와 같은 탐색 알고리즘을 주로 배우는 것이 아닌 이번 Chapter에서는 Chapter 08에서 배운 트리의 연장선이라 볼 수 있다.
따라서 굳이 따지자면 탐색은 알고리즘이라기 보단 자료구조에 더 가까운 주제다.
효율적인 탐색을 위해서는 '어떻게 찾을까'만 생각하는 것이 아닌 '효율적인 탐색을 위한 저장방법이 무엇일까'에 대해 우선 고민해야한다.
그리고 이 효율적인 탐색이 가능한 대표적인 저장 방법은 '트리'다.
이 다음 Chapter에서는 '테이블과 해쉬'에 관해 배우게 되는데 이도 탐색과 관련이 있는 내용이다.
앞에서 배운 정렬도 탐색을 목적으로 하는 경우가 대부분인 만큼 탐색은 자료구조에서 (더 넓게는 컴퓨터 공학에서) 매우 중요한 부분을 차지하고 있다.
보간 탐색 (Interpolation Search)
'보간 탐색(interpolation search)'은 앞에서 배운 순차 탐색(정렬되지 않은 대상을 기반으로 하는 탐색)과 이진 탐색(정렬된 대상을 기반으로 하는 탐색) 중에서 이진 탐색의 비효율성을 개선시킨 알고리즘이다.
이진 탐색은 중앙에 위치한 데이터를 탐색한 후 이를 기준으로 탐색 탐색을 진행하는 알고리즘이다.
찾는 대상이 중앙에 위치하든 맨 앞에 위치하던 상관하지 않고 일관되게 반씩 줄여가면서 탐색을 진행해 나간다.
때문에 찾는 대상의 위치에 따라서 탐색의 효율에 차이가 발생했다.
보간 탐색은 이진 탐색처럼 그냥 중앙에서 탐색을 시작하는 것이 아닌 탐색 대상이 앞쪽에 위치해 있으면 앞쪽에서 탐색을 시작하는 것이다.
예를 들어 오른차순으로 정렬된 배열을 대상으로 앞쪽에 위치한 데이터를 찾고자 할 때 이진 탐색과 보간 탐색의 첫 번째 탐색 위치는 다음과 같이 차이가 난다.
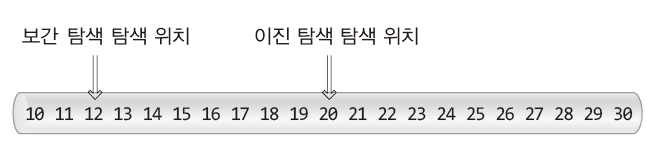
위 그림은 정수 12를 찾을 때의 첫 번째 탐색위치를 보여준다.
이진 탐색은 값에 상관없이 탐색위치를 결정하지만 보간 탐색은 그 값이 상대적으로 앞에 위치한다고 판단하면 앞쪽에서 탐색을 진행한다.
따라서 '데이터'와 데이터가 저장된 위치의 '인덱스 값'이 직선의 형태로 비례하면(선형의 형태로 비례하면), 보간 탐색의 경우 단번에 데이터를 찾기도 한다.
단번에 찾지 못하더라도 탐색의 위치가 찾는 데이터와 가깝기 때문에 탐색 대상을 줄이는 속도가 이진 탐색보다 뛰어나다.
이제 고민해야하는 것은 보간 탐색의 탐색위치를 결정하는 방법이다.
이는 수학적으로 접근할 수 있다.
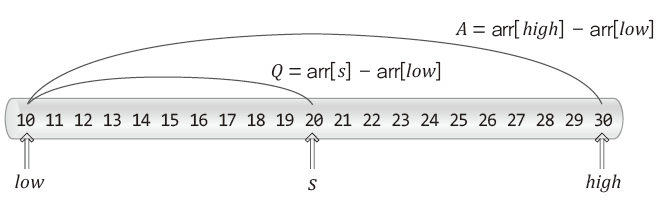
위 그림에서 와 는 탐색대상의 시작과 끝에 해당하는 인덱스 값이고, 는 찾는 데이터가 저장된 위치의 인덱스 값이다.
그런데 보간 탐색은 데이터의 값과 그 데이터가 저장된 위치의 인덱스 값이 비례한다고 가정하기 때문에 위 그림을 근거로 다음의 비례식을 구성한다.
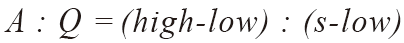
이 식에서 는 찾고자 하는 데이터의 인덱스 값이므로 위의 비례식을 에 대한 식으로 다음과 같이 정리할 수 있다.
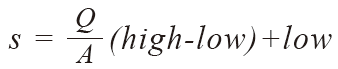
그리고 찾는 데이터의 값 를 라 하면 위의 식은 최종적으로 다음과 같이 정리가 된다.
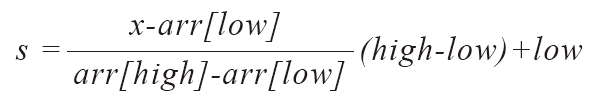
이로써 찾는 값을 에 삽입하여 탐색위치 를 구하는 식을 얻을 수 있다.
이 식은 단순하지만 나눗셈 연산이 들어가고 오차율을 최소화하기 위해서 정수형 나눗셈이 아닌 실수형 나눗셈을 한다는 것에 주목해야 한다.
이는 보간 탐색의 단점이기 때문이다.
탐색 키 (Search Key)와 탐색 데이터 (Search Data)
위에서 설명한 보간탐색의 원리를 구현할 차례다.
보간 탐색의 구현에 앞서 구조체 하나를 살펴보자.
typedef int key; // 탐색 티에 대한 typedef 선언
typedef double Data; // 탐색 데이터에 대한 typedef 선언
typedef struct item
{
key searchKey; // 탐색 키 (search key)
Data searchData; // 탐색 데이터 (search data)
} Item;여기서 정의된 구조체 Item의 멤버는 '탐색 키'와 '탐색 데이터'로 이루어져 있다.
예를 들어 '사번이 7인 직원의 정보를 찾는다'고 했을 때 사번이 '탐색 키 (search key)'가 디고 직원의 정보가 '탐색 데이터 (search data)'가 된다.
때문에 일반적인 상황에서는 위의 구조체 정의에서 보이듯이 탐색 키와 탐색 데이터를 묶는 형태의 구조체를 정의하게 되고, 정렬이나 탐색이나 그 탐색의 대상을 탐색 키에 맞추게 된다.
실제 프로그램 개발에 있어서 탐색의 대상은 데이터가 아닌 키이고 학습의 편의를 위해 여태까지는 데이터를 찾는 형태로 배웠을 뿐이다.
그리고 중요하게 기억해야 하는 부분은 "탐색 키는 그 값이 고유해야 한다"는 것이다.
키에는 그 값이 유일하다는 의미가 담겨 있고 NULL과 같은 값이 채워질 수 없다는 의미도 담겨있다.
보간 탐색의 구현
이론적으로 보간 탐색과 이진 탐색의 유일한 차이점은 탐색의 대상을 선정하는 방법에 있다.
따라서 보간 탐색 구현을 위해 이진 탐색을 다시 한번 살펴보자.
(이진 탐색이 잘 기억 나지 않는다면 Chapter 02. 재귀(Recursion)글을 다시 한번 읽어 보자.😉)
// RecursiveBinarySearch.c
#include <stdio.h>
int BSearchRecur(int ar[], int first, int last, int target)
{
int mid;
if(first > last)
return -1; // -1의 반환 = 탐색의 실패
mid = (first+last)/2; // 탐색 대상의 중앙 찾기.
if(ar[mid]==target)
return mid; // 탐색된 타겟의 인덱스 값 반환.
else if(target < ar[mid])
return BSearchRecur(ar, first, mid-1, target);
else
return BSearchRecur(ar, mid+1, last, target);
}
int main()
{
....
return 0;
}BSearchRecur 함수는 mid = (first + last) / 2; 문장을 통해서 탐색의 위치를 계산한다.
그런데 이진 탐색과 보간 탐색의 유일한 차이점은 탐색의 대상을 선택하는 방법에 있으니 이를 아까 구한 찾고자 하는 데이터의 인덱스 값 구하는 정리로 바꾸면 보간 탐색의 구현이 완료가 된다.

위의 문장에서는 나눗셈의 피연산자를 double 형으로 형 변환하여 모든 연산들이 실수형으로 진행되어 오차를 최소화하도록 했다.
그럼 완성된 보간 탐색 구현 코드를 살펴보자.
#include <stdio.h>
int ISearch(int ar[], int first, int last, int target)
{
int mid;
if(first > last)
return -1; // -1의 반환 = 탐색의 실패
// 보간 탐색의 탐색 대상 선택 방법
mid = ((double)(target-ar[first]) / (ar[last]-ar[first]) * (last-first)) + first;
if(ar[mid]==target)
return mid; // 탐색된 타겟의 인덱스 값 반환.
else if(target < ar[mid])
return ISearch(ar, first, mid-1, target);
else
return ISearch(ar, mid+1, last, target);
}
int main()
{
int arr[] = {1, 3, 5, 7, 9};
int idx;
idx = ISearch(arr, 0, sizeof(arr)/sizeof(int)-1, 7);
if(idx==-1)
printf("search fail. \n");
else
printf("target index: %d \n", idx);
idx = ISearch(arr, 0, sizeof(arr)/sizeof(int)-1, 10);
if(idx==-1)
printf("search fail. \n");
else
printf("target index: %d \n", idx);
return 0;
}
> 출력
target index: 3
search fail.여기서 만약에 배열에 저장되어 있지 않은 2를 찾으려고 하면 main 함수를 대상으로 ISearch 함수가 제대로 동작하지 않는다.
문제는 ISearch 함수의 if(first > last) return -1;이라는 탈출조건을 만족시키지 못해서 발생한 오류다.
따라서 오류를 해결하기 위해서 함수의 탈출조건을 if(ar[first]>target || ar[last]<target) return -1;로 변경해야 한다.
탐색대상이 존재하지 않는 경우 ISearch 함수가 재귀적으로 호출됨에 따라 target에 저장된 값은 first와 last가 가리키는 값의 범위를 넘어서게 된다.
정렬된 탐색대상의 범위를 좁혀가면서 정렬을 진행하기 때문에 당연히 발생하는 현상이다.
따라서 이러한 특성을 기반으로 변경된 탈출조건과 같이 구성해야 한다.
탈출 조건을 만족하지 않는 이유
우선, 탈출 조건이 만족되지 않는 상황에 대해서 알아보자.
다음과 같이 ISearch 함수가 호출되었다고 가정해보자.
int main()
{
int arr[] = {1, 3, 5, 7, 9};
....
ISearch(arr, 1, 4, 2); // 배열 arr의 인덱스 1~4 범위 내에서 2 탐색
....
}위와 같이 ISearch 함수가 호출되는 상황을 인위적으로 만들면 탐색위치를 계산하는 다음 문장에 값을 대입해 봤을 때 mid에 0이 저장됨을 알 수 있다.
인덱스 1~4의 범위 내에서 최댓값과 최솟값은 각각 3과 9다.
그런데 타겟은 2다.
즉, 그 값이 탐색 범위 내에 위치하지 못할 만큼 작다.
그러니 가장 왼쪽에 있는 값과 비교하라는 의미로 0을 반환하는 것이 맞지 않을까?
하지만 이 결과가 다음에 오는 코드들과 결합되면서 문제가 된다.
if(ar[mid]==target)
return mid; // 탐색된 타겟의 인덱스 값 반환.
else if(target < ar[mid])
return ISearch(ar, first, mid-1, target);
else
return ISearch(ar, mid+1, last, target); // 이 문장이 실행됨.조건에 의해서 마지막 else 구문의 ISearch 함수 호출문이 실행이 되면서 무한루프에 빠지게 된다.
그래서 아까 변경한 조건과 같이 '탐색 대상이 존재하지 않을 경우, 탐색 대상의 값은 탐색 범위의 값을 넘어선다'라고 수정해준 것이다.
11-2. 이진 탐색 트리
이번에 배울 이진 탐색 트리는 앞에서 배운 이진 트리 바탕의 탐색에 효율적인 자료구조다.
이진 탐색 트리의 이해
이진 트리의 구조를 보면 저장된 데이터의 수가 10억 개가 된다고 해도 트리의 높이는 30을 넘지 않는다는 것을 보아 탐색에 있어 효율적이라는 것을 금방 알 수 있다.
즉, 데이터에 이르는 길을 알고 있다면 루트 노드에서부터 단말 노드에 이르기까지 총 30개 노드를 지나는 과정에서 원하는 데이터를 찾을 수 있다는 것이다.
따라서 이진 트리는 단말 노드에 이르는 길의 갈래가 매우 많기 때문에 찾는 데이터가 존재하는 제대로 된 길을 선택할 수 있어야 한다.
이진 탐색 트리에는 데이터를 저장하는 규칙이 있어 그 규칙은 특정 데이터의 위치를 찾는데 사용할 수 있다.
쉽게 말해서 이진 트리에 데이터 저장 규칙을 더해놓은 것이 이진 탐색 트리다.
이진 탐색 트리에는 몇 가지 조건이 있는데 참고로 '탐색 키'는 정수라 가정하였고 이러한 탐색 키를 간단하게 키라고 언급했다.
- 이진 탐색 트리의 노드에 저장된 키는 유일하다.
- 루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 크다.
- 루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키보다 작다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리다.
이러한 조건들을 만족하는 트리의 예시를 하나 보자.
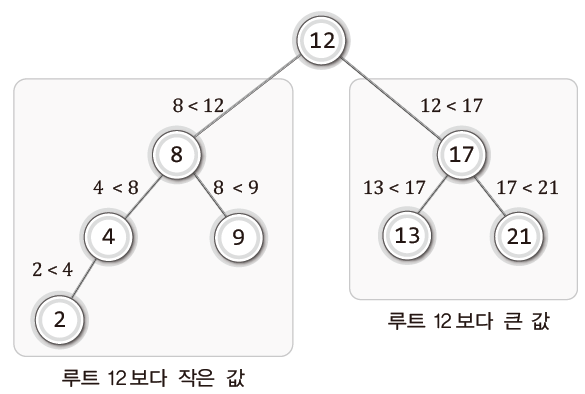
위 그림에서 볼 수 있듯 루트 노드의 왼쪽 서브 트리에 저장된 값들은 12보다 작고,
오른쪽 서브 트리에 저장된 값들은 12보다 크다. (왼쪽 자식 노드의 키 < 부모 노드의 키 < 오른쪽 자식 노드의 키)
그리고 이 수식이 이진 탐색 트리의 구현에 더 직접적으로 도움이 되는 결론이다.
예를 들어 위 이진 탐색 트리를 대상으로 숫자 10을 저장한다고 가정하자.
그러면 루트 노드를 시작으로 다음의 과정을 거쳐 저장될 위치를 결정하게 된다.
- 10 < 12 : 왼쪽 자식노드로 이동
- 10 > 8 : 오른쪽 자식 노드로 이동
- 10 > 9 : 오른쪽 자식 노드로 이동
- 아무것도 없으니 그 위치에 저장.
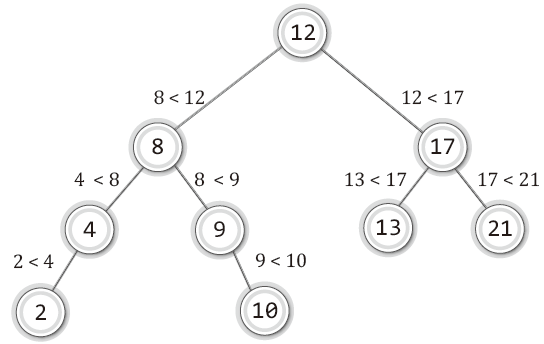
따라서 위 그림과 같이 10이 위치하게 된다.
이진 탐색 트리는 작으면 왼쪽, 크면 오른쪽으로 라는 원칙을 기준으로 데이터를 삽입하고 탐색한다.
이진 탐색 트리의 구현
이진 탐색 트리를 구현할 수 있는 방법에는 2가지가 있다.
- 이전에 구현한 이진 트리를 참조하여 처음부터 완전히 다시 구현.
- 이전에 구현한 이진 트리를 활용하여 구현.
우선 첫 번째 방법을 이용하면, 이전에 공부한 이진 트리의 이해 없이 코드를 바로 분석할 수 있다. 그리고 이전에 경험했던 이진 트리를 코드 레벨에서 다시 한번 복습할 수 있다.
(이것들이 과연 장점일까...?😂)
두 번째 방법을 이용하면, 이진 탐색 트리가 이진 트리의 확장이라는 사실을 코드 레벨에서 확인할 수 있다.
앞서 구현한 이진 탐색 트리를 점검하는 기회가 되며, 이진 트리의 ADT를 통해서 정의한 함수들이 기능적으로 부족한 부분에 있어 코드 리펙토링할 수 있다.
이진 트리를 활용한 이진 탐색 트리의 구현을 경험하는 것은 좋은 프로그래밍 모델을 경험하는 기회도 된다.
사실 이전에도 이진 트리를 활용하여 이진 트리의 일종인 '수식 트리'를 구현한 경험이 있다.
그때 활용한 방법을 이번에도 적용하여 이진 탐색 트리를 구현해볼 것이다.
그러기 위해서는 이전에 작성한 파일 2개가 필요하다.
- BinaryTree2.h : 이진 트리 정의한 헤더파일
- BinaryTree2.c : 이진 트리 구현한 소스파일
헤더파일(BinaryTree2.h) 선언된 함수들에 대해서도 다시 한번 간단하게 리마인드 해보자.
BTreeNode * MakeBTreeNode(void);
: 노드를 동적으로 할당해서 그 노드의 주소 값을 반환BTData GetData(BTreeNode * bt);
: 노드에 저장된 데이터를 반환void SetData(BTreeNode * bt, BTData data);
: 인자로 전달된 데이터를 노드에 저장BTreeNode * GetLeftSubTree(BTreeNode * bt);
: 인자로 전달된 노드의 왼쪽 자식 노드의 주소 값을 반환BTreeNode * GetRightSubTree(BTreeNode * bt);
: 인자로 전달된 노드의 오른쪽 자식 노드의 주소 값을 반환void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
: 인자로 전달된 노드의 왼쪽 자식 노드를 교체void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
: 인자로 전달된 노드의 오른쪽 자식 노드를 교체
이제 이 함수들을 이용해서 이진 트리의 일종인 이진 탐색 트리를 구현해보자.
1) 헤더파일 (BinarySearchTree.h)
#ifndef __BINARY_SEARCH_TREE_H__
#define __BINARY_SEARCH_TREE_H__
#include "BinaryTree2.h"
typedef BTData BSTData;
// BST의 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot);
// 노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode * bst);
// BST를 대상으로 데이터 저장(노드의 생성과정 포함)
void BSTInsert(BTreeNode ** pRoot, BSTData data);
// BST를 대상으로 데이터 탐색
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target);
#endif이진 탐색 트리의 핵심 연산 세 가지는 다른 자료구조들과 마찬가지로 삽입, 삭제, 그리고 탐색이다.
그런데 삭제는 별도로 고민해야 할 문제이기 때문에 우선 삽입과 탐색에 대한 함수를 각각 정의했다.
- 삽입 :
void BSTInsert(BTreeNode ** pRoot, BSTData data) {...} - 탐색 :
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target) {...}
간단한 main 함수를 통해서 위 두 함수와 헤더파일에 선언된 또 다른 두 함수의 사용방법을 살펴보자. (실제로 실행파일을 만들진 않을 것이다. 실제 실행파일은 소스파일 작성 이후 만들 예정.)
int main(void)
{
BTreeNode * bstRoot; // bstRoot는 BST의 루트 노드를 가리킨다.
BTreeNode * sNode;
BSTMakeAndInit(&bstRoot); // Binary Search Tree의 생성 및 초기화
BSTInsert(&bstRoot, 1); // bstRoot에 1을 저장
BSTInsert(&bstRoot, 2); // bstRoot에 2을 저장
BSTInsert(&bstRoot, 3); // bstRoot에 3을 저장
// 1 탐색
sNode = BSTSearch(bstRoot, 1);
if(sNode == NULL)
printf("search fail. \n");
else
printf("key value: %d \n", BSTGetNodeData(sNode));
return 0;
}위 main 함수에서 보이듯이 다음과 같이 BSTMakeAndInit 함수가 호출되고 나면, 이진 탐색 트리의 생성 및 초기화가 완료된 것으로 간주한다.
그때부터 bstRoot는 생성된 이진 탐색 트리를 지칭하는 이름이 된다.
그래서 트리에 데이터를 추가할 때는 다음과 같이 BSTInsert(&bstRoot, 1); 함수를 호출한다.
이진 탐색 트리에 데이터를 저장하기 위해서 직접 노드를 생성할 필요가 없다.
노드의 생성과 위치 선정 및 저장은 BSTInsert 함수 내에서 이뤄지기 때문이다.
탐색도 유사한 방법으로 진행된다.
sNode = BSTSearch(bstRoot, 1); 문장이 실행되고 탐색의 결과, 목표한 대상을 찾았다면 이를 저장하고 있는 노드의 주소 값이 반환된다.
그리고 main 함수에서 보였듯이 BSTGetNodeData 함수를 통해서 노드에 저장된 값을 얻을 수도 있다.
2) 소스파일
[1] 삽입과 탐색 (BinarySearchTree.c)
이진 탐색 트리에서 삽입과 탐색은 어렵지 않다.
그래도 몇몇 사례를 통해서 그 과정을 살펴보자.
먼저 세 개의 노드로 구성된 트리에 숫자 11과 10의 추가과정을 순서대로 보자.
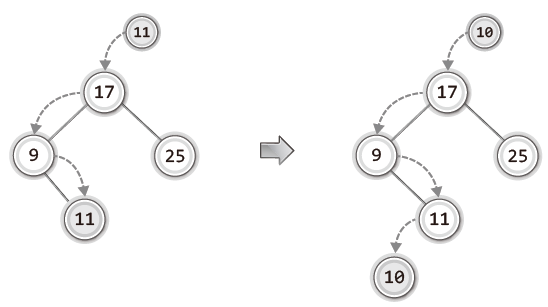
비교대상보다 값이 작으면 왼쪽 자식 노드로, 값이 크면 오른쪽 자식 노드로 이동하는데 여기서 추가로 알아야 할 점이 "비교대상이 없을 때까지 내려가고, 비교대상이 없는 그 위치가 새 데이터가 저장될 위치다."라는 것이다.
위 그림에 이어서 29와 22를 저장하는 예를 살펴보자.
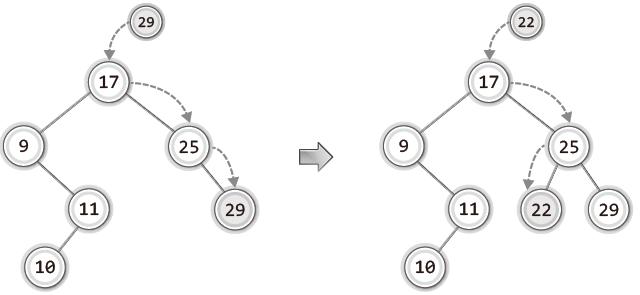
여기서도 동일한 규칙이 적용되어 데이터들이 저장되는 것을 확인할 수 있다.
이제 새 데이터의 저장을 담당하는 BSTInsert 함수에 대해 알아보자.
void BSTInsert(BTreeNode ** pRoot, BSTData data)
{
BTreeNode * pNode = NULL; // parent node
BTreeNode * cNode = *pRoot; // current node
BTreeNode * dNode = NULL; // new node
// 새로운 노드(새 데이터 담긴 노드)가 추가될 위치 찾기
while(cNode != NULL)
{
if(data == GetData(cNode))
return; // already inserted
pNode = cNode;
if(GetData(cNode) > data)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
// pNode의 자식 노드로 추가할 새 노드의 생성
nNode = MakeBTreeNode(); // 새 노드 생성
SetData(nNode, data); // 새 노드에 데이터 저장
// pNode의 자식 노드로 새 노드를 추가
if(pNode != NULL) // 새 노드가 루트 노드가 아니라면
{
if(data < GetData(nNode))
MakeLeftSubTree(pNode, nNode);
else
MakeRightSubTree(pNode, nNode);
}
else // 새 노드가 루트 노드라면
{
*pRoot = nNode;
}
}여기서 while문의 역할은 저장할 값의 크기에 따라 왼쪽 또는 오른쪽 자식 노드로 이동하면서 새 노드의 저장위치를 찾는 것이다.
따라서 이 while문을 빠져나오면 cNode에는 새 노드가 저장될 위치정보가 담긴다.
그런데 이 위치에 노드를 저장하기 위해 필요한 것은 이 위치를 자식으로 하는 부모 노드의 주소 값이다. (부모 노드에 자식 노드의 주소 값이 저장되기 때문이다.)
실제로 이어지는 if~else 구문에서 부모 노드의 주소 값이 담긴 pNode를 기반으로 자식 노드가 추가되고 있다.
이어서 탐색을 담당하는 BSTSearch 함수를 보자.
탐색의 과정은 삽입의 과정을 근거로 하기에 별도의 설명이 필요 없을 것이다.
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target)
{
BTreeNode * cNode = bst; // current node
BSTData cd; // current data
while(cNode != NULL)
{
cd = GetData(cNode);
if(target == cd)
return cNode;
else if(target < cd)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
return NULL; // 탐색대상이 저장되어 있지 않음.
}위 함수에 삽입된 while문에서도 비교대상의 노드보다 값이 작으면 왼쪽 자식 노드로, 값이 크면 오른쪽 자식 노드로 이동하고 있다.
그럼에도 불구하고 찾는 데이터가 없으면 NULL을 반환하도록 했다.
위 내용과 BST를 초기화 하는 함수, 데이터를 가져오는 함수 등을 추가로 소스파일을 정리하면 아래와 같다.
#include <stdio.h>
#include "BinaryTree2.h"
#include "BinarySearchTree.h"
void BSTMakeAndInit(BTreeNode ** pRoot)
{
*pRoot = NULL;
}
BSTData BSTGetNodeData(BTreeNode * bst)
{
return GetData(bst);
}
void BSTInsert(BTreeNode ** pRoot, BSTData data)
{
BTreeNode * pNode = NULL; // parent node
BTreeNode * cNode = *pRoot; // current node
BTreeNode * nNode = NULL; // new node
// 새로운 노드(새 데이터 담긴 노드)가 추가될 위치 찾기
while(cNode != NULL)
{
if(data == GetData(cNode))
return; // already inserted
pNode = cNode;
if(GetData(cNode) > data)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
// pNode의 자식 노드로 추가할 새 노드의 생성
nNode = MakeBTreeNode(); // 새 노드 생성
SetData(nNode, data); // 새 노드에 데이터 저장
// pNode의 자식 노드로 새 노드를 추가
if(pNode != NULL) // 새 노드가 루트 노드가 아니라면
{
if(data < GetData(pNode))
MakeLeftSubTree(pNode, nNode);
else
MakeRightSubTree(pNode, nNode);
}
else // 새 노드가 루트 노드라면
{
*pRoot = nNode;
}
}
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target)
{
BTreeNode * cNode = bst; // current node
BSTData cd; // current data
while(cNode != NULL)
{
cd = GetData(cNode);
if(target == cd)
return cNode;
else if(target < cd)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
return NULL; // 탐색대상이 저장되어 있지 않음.
}- 실행파일 (BinarySearchTreeMain.c)
위 함수들이 제대로 잘 작동하는지 확인하기 위한 실행파일은 다음과 같다.
#include <stdio.h>
#include "BinarySearchTree.h"
int main()
{
BTreeNode * bstRoot;
BTreeNode * sNode;
BSTMakeAndInit(&bstRoot);
BSTInsert(&bstRoot, 9);
BSTInsert(&bstRoot, 1);
BSTInsert(&bstRoot, 6);
BSTInsert(&bstRoot, 2);
BSTInsert(&bstRoot, 8);
BSTInsert(&bstRoot, 3);
BSTInsert(&bstRoot, 5);
sNode = BSTSearch(bstRoot, 1);
if(sNode == NULL)
printf("search failed.\n");
else
printf("key data : %d\n", BSTGetNodeData(sNode));
sNode = BSTSearch(bstRoot, 4);
if(sNode == NULL)
printf("search failed.\n");
else
printf("key data : %d\n", BSTGetNodeData(sNode));
sNode = BSTSearch(bstRoot, 6);
if(sNode == NULL)
printf("search failed.\n");
else
printf("key data : %d\n", BSTGetNodeData(sNode));
sNode = BSTSearch(bstRoot, 7);
if(sNode == NULL)
printf("search failed.\n");
else
printf("key data : %d\n", BSTGetNodeData(sNode));
return 0;
}
> gcc .\BinarySearchTree.c .\BinarySearchTreeMain.c .\BinaryTree2.c
> .\a.exe
> 출력
key data : 1
search failed.
key data : 6
search failed.위 main 함수에서는 이진 탐색 트리에 다수의 값을 저장한 다음에 그 값의 저장유무를 확인하는 정도에서 마무리했다.
다음에 배울 내용은 트리의 순회를 이용해서 트리에 저장된 값을 전반적으로 확인해 볼 것이다.
[2] 삭제 1 : 이론적 설명과 일부 구현
이진 탐색 트리의 삭제는 단순하지 않은데 그 과정이 복잡한 이유 대해서 알아보자.
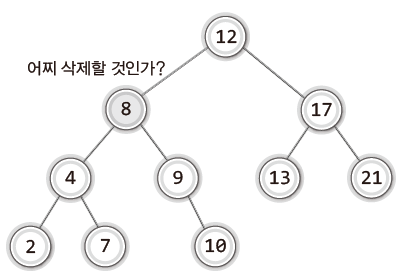
위 이진 탐색 트리에서 8이 담긴 노드를 삭제한다고 가정해보자.
이 상황에서 그냥 이 노드만 삭제하면 그만일까?
그 자리를 누군가 대신 채워줘야만 이진 탐색 트리가 유지된다.
즉, 이진 탐색 트리에서 임의의 노드를 삭제하는 경우, 삭제 후에도 이진 탐색 트리가 유지되도록 빈자리를 채워야되기 때문에 어려운 것이다.
물론 모든 삭제의 경우에 있어서 이 문제를 고민해야 하는 것은 아니다.
삭제 대상이 단말 노드라면 간단하지만, 단말노드가 아니라면 무엇으로 대신할지 고민해야 한다.
이진 탐색 트리의 삭제에 대한 경우의 수는 다음과 같다.
- 상황 1) 삭제할 노드가 단말 노드인 경우
- 상황 2) 삭제할 노드가 하나의 자식 노드(하나의 서브 트리)를 갖는 경우
- 상황 3) 삭제할 노드가 두 개의 자식 노드(두 개의 서브 트리)를 갖는 경우
이렇게 삭제에 대한 경우의 수는 세 가지다.
하지만 구현방법에 따라서 삭제 대상이 루트 노드인 경우와 그렇지 않은 경우를 나눠야 하기 때문에 삭제에 대한 경우의 수는 최대 여섯 가지로 구분할 수도 있다.
이제 상황별 삭제 방법을 그림을 통해 이해해보자.
- 상황 1) 삭제할 노드가 단말 노드인 경우
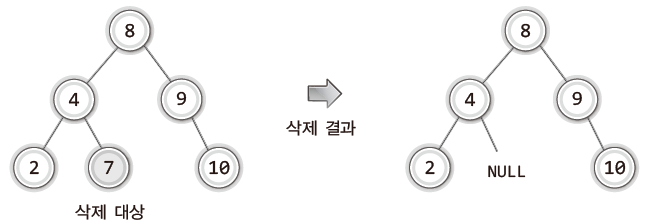
삭제 대상인 단말 노드를 삭제하는 것으로 삭제 과정이 완료되기 때문에 비교적 간단하며 코드로 구현하면 다음과 같다.
// dNode와 pNode는 각각 삭제할 노드와 이의 부모 노드를 가리키는 포인터 변수
if(삭제할 노드가 단말 노드)
{
if(GetLeftSubTree(pNode) == dNode) // 삭제할 노드가 왼쪽 자식 노드라면
RemoveLeftSubTree(pNode); // 왼쪽 자식 노드 트리에서 제거
else
RemoveRightSubTree(pNode); // 오른쪽 자식 노드 트리에서 제거
}위에서 호출한 Remove~ 로 시작하는 두 함수는 아직 정의한 바 없는 함수들인데,
이들에 대해서는 잠시 후 선언 및 정의할 예정이고 각각의 함수호출이 의미하는 바는 다음과 같다.
- RemoveLeftSubTree(pNode) : pNode가 가리키는 노드의 왼쪽 자식 노드 트리에서 제거
- RemoveRightSubTree(pNode) : pNode가 가리키는 노드의 오른쪽 자식 노드 트리에서 제거
- 상황 2) 삭제할 노드가 하나의 자식 노드(하나의 서브 트리)를 갖는 경우
이 상황 역시 비교적 쉽다.
상황 1에서 부모 노드와 자식 노드를 연결하는 작업만 추가하면 된다.

하지만 여기에도 한 가지 주의해야할 사항이 있다.
위 그림의 왼쪽 트리에서 10이 저장된 노드가 왼쪽 자식 노드이건 오른쪽 자식 노드이건 이에 상관 없이 10이 저장된 노드는 8이 저장된 노드의 오른쪽 자식 노드가 되어야 한다.
따라서 이를 코드로 구현하면 다음과 같다.
// dNode와 pNode는 각각 삭제할 노드와 이의 부모 노드를 가리키는 포인터 변수
if(삭제할 노드가 하나의 자식 노드 갖고 있음)
{
BTreeNode * dcNode; // 삭제 대상의 자식 노드를 가리키는 포인터 변수
// 삭제 대상의 자식 노드 찾기
if(GetLeftSubTree(dNode) != NULL) // 자식 노드가 왼쪽에 있다면
dcNode = GetLeftSubTree(dNode);
else
dcNode = GetRightSubTree(dNode);
// 삭제 대상의 부모 노드와 자식 노드를 연결
if(GetLeftSubTree(pNode) == dNode) // 삭제 대상이 왼쪽 자식 노드라면
ChangeLeftSubTree(pNode, dcNode); // 왼쪽으로 연결
else // 삭제 대상이 오른쪽 자식 노드라면
ChangeRightSubTree(pNode, dcNode); // 오른쪽으로 연결
}위 코드에서도 Change~로 시작하는 두 함수는 아직 정의한 바 없는 함수들인데,
이들에 대해서도 잠시 후 선언 및 정의할 예정이고 각각의 함수호출이 의미하는 바는 다음과 같다.
- ChangeLeftSubTree : MakeLeftSubTree 함수와 유사한 함수
- ChangeRightSubTree : MakeRightSubTree 함수와 유사한 함수
위의 두 함수와 BinaryTree2.h에 선언된 Make~로 시작하는 두 함수와의 유일한 차이점은,
기존 자식 노드의 메모리 소멸 과정을 동반하느냐 안하느냐에 있다.
- 상황 3) 삭제할 노드가 두 개의 자식 노드(두 개의 서브 트리)를 갖는 경우
마지막 상황을 살펴보기 위해 다음 그림을 보면서 삭제로 인해 비는 위치를 무엇으로 채울지 한번 생각해보자.
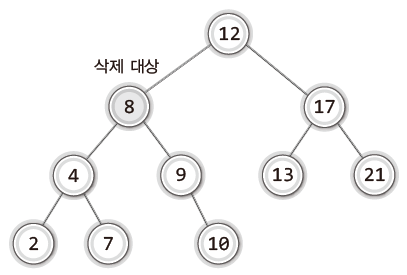
8을 삭제하는 경우 이를 대체할 후보로 다음 두 개의 노드를 꼽을 수 있다.
- 8이 저장된 노드의 왼쪽 서브 트리에서 가장 큰 값인 7을 저장한 노드
- 8이 저장된 노드의 오른쪽 서브 트리에서 가장 작은 값인 9를 저장한 노드
삭제 대상을 7 또는 9를 저장한 노드로 각각 대체했을 때의 결과는 다음과 같다.
| 7이 저장된 노드로 대체한 경우 | 9가 저장된 노드로 대체한 경우 |
|---|---|
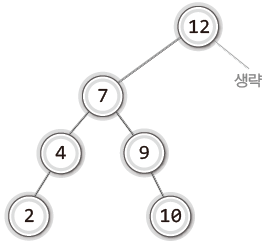 | 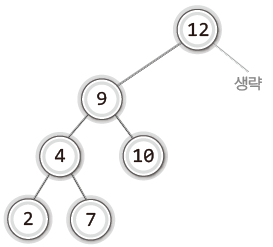 |
이렇듯 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 값이나, 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값을 저장한 노드로 대체하면 된다.
서브 트리에서 가장 큰 값이나 가장 작은 값을 저장한 노드를 찾는 것은 어렵지 않다.
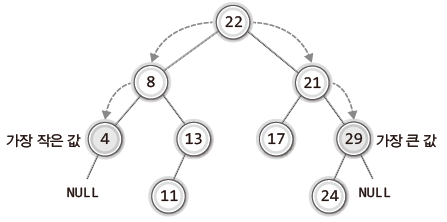
가장 큰 값을 찾을 때는 NULL을 만날 때까지 계속해서 오른쪽 자식 노드로 이동하면 되고,
가장 작은 값을 찾을 때는 NULL을 만날 때까지 계속해서 왼쪽 자식 노드로 이동하면 된다.
위 두 가지 방법 중 "삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값을 지니는 노드를 찾아서 이것으로 삭제할 노드를 대체하는 것"을 선택할 것이다.
이 방법으로 이진 탐색 트리의 삭제 전과 후의 모습을 보면 다음과 같다.
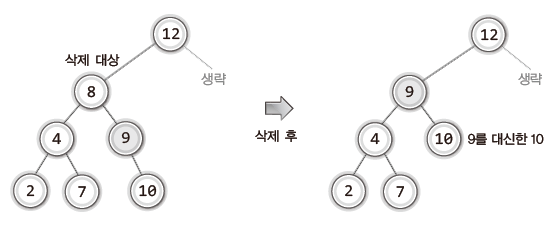
삭제의 결과를 이루기 위해 해야 할 일은 다음과 같다.
삭제가 되는 8이 저장된 노드를 9가 저장된 노드로 대체한다.
그리고 이로 인해서 생기는 빈자리는 9가 저장된 노드의 자식 노드로 대체한다.
위 과정을 위해 8이 저장된 노드의 위치에 9가 저장된 노드를 가져다 놓지 않고,
값의 대입을 통해 노드의 교체를 대신하는 방법을 적용할 것이다.
이 방법을 사용하게 되면, 삭제 대상인 8이 저장된 노드의 부모 노드와 자식 노드의 연결을 위해서 별도의 코드를 삽입할 필요가 없어지기 때문에 여러모로 편리하다.
위 과정을 다시 한번 정리하면 다음과 같다.
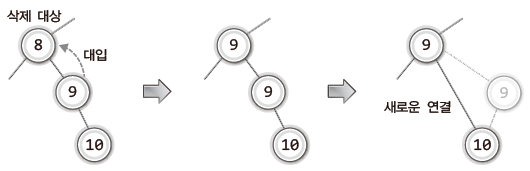
- 단계 1) 삭제할 노드를 대체할 노드 찾기
- 단계 2) 대체할 노드에 저장된 값을 삭제할 노드에 대입
- 단계 3) 대체할 노드의 부모 노드와 자식 노드 연결
이 단계들을 코드로 구현하면 다음과 같다.
// dNode와 pNode는 각각 삭제할 노드와 이의 부모 노드를 가리키는 포인터 변수
if(삭제할 노드가 두 개의 자식 노드 갖고 있음)
{
BTreeNode * mNode = GetRightSubTree(dNode); // mNode는 대체 노드
BTreeNode * mpNode = dNode; // mpNode는 대체 노드의 부모 노드
// 단계 1
while(GetLeftSubTree(mNode) != NULL)
{
mpNode = mNode;
mNode = GetLeftSubTree(mNode);
}
// 단계 2
SetData(dNode, GetData(mNode));
// 단계 3
if(GetLeftSubTree(mpNode) == mNode) // 대체할 노드가 왼쪽 자식 노드라면
{
// 대체할 노드의 자식 노드를 부모 노드의 왼쪽에 연결
ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
}
else // 대체할 노드가 오른쪽 자식 노드라면
// 대체할 노드의 자식 노드를 부모 노드의 오른쪽에 연결
ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
}단계 3에서 GetRightSubTree 함수가 두 번 호출된 것이 어색하다고 생각이 들 수 있다.
이 중 하나는 GetLeftSubTree 함수가 호출되어야 뭔가 짝이 맞을거 같다는 생각이다.
하지만 대체할 노드의 자식 노드는 항상 오른쪽에 존재하기 때문에 이 코드가 맞다.
삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값을 지니는 노드를 찾아서 이것으로 삭제할 노드를 대체하기 때문에 가장 값을 지니는 노드를 찾으려면 NULL을 만날 때까지 왼쪽 자식 노드로 계속해서 이동해야 한다.
그리고 그 노드이에 자식 노드가 있다면 그것은 오른쪽 노드일 것이기 때문이다!
[3] 삭제 2 : 이진 트리 확장
삭제를 포함한 이진 탐색 트리의 완성을 위해서 우선 BinaryTree2.h와 BinaryTree2.c에 다음 네 개의 함수를 추가로 선언 및 정의하려 한다.
BTreeNode * RemoveLeftSubTree(BTreeNode * bt);
: 왼쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값 반환BTreeNode * RemoveRightSubTree(BTreeNode * bt);
: 오른쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값 반환void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub);
: 메모리 소멸을 수반하지 않고 main의 왼쪽 자식 노드를 변경void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub);
: 메모리 소멸을 수반하지 않고 main의 오른쪽 자식 노드를 변경
이전에 구현한 이진 탐색 트리는 이미 구현한 이진 트리의 함수만으로는 그 도구가 충분하지 않았다.
노드의 제거에 대한 기능이 정의되지 않았고, MakeLeftSubTree와 MakeRightSubTree 함수는 교체되는 노드의 소멸까지 진행했기 때문이다.
그래서 단순히 자식 노드의 교체를 목적으로 함수 두 가지를 추가로 정의했다.
그리고 당시에는 이진 트리의 구성에 초점을 맞췄기 때문에 삭제에 대한 기능을 정의하지 않았다.
삭제에 관련된 함수 두 가지를 추가로 정의했다.
이 네 가지 함수를 구현하면 다음과 같다.
// 왼쪽 자식 노드 제거, 제거된 노드의 주소 값 반환
BTreeNode * RemoveLeftSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->left;
bt->left = NULL;
}
return delNode;
}
// 오른쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값 반환
BTreeNode * RemoveRightSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->right;
bt->right = NULL;
}
return delNode;
}
// 메모리 소멸을 수반하지 않고 main의 왼쪽 자식 노드를 변경
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
main->left = sub;
}
// 메모리 소멸을 수반하지 않고 main의 오른쪽 자식 노드를 변경
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
main->right = sub;
}보통 삭제 또는 제거라고 하면 반드시 메모리의 해제까지 담당해야 한다고 생각하는 경우가 많다.
하지만 삭제와 메모리의 해제는 별개의 것이며 삭제 과정에서 메모리의 해제를 포함하는 경우도 있지만 반드시 필요한 것은 아니며 포함해서는 안되는 경우도 존재한다.
위에 새로 정의한 함수 네 가지는 BinaryTree3.h와 BinaryTree3.c로 기존 함수에 더해서 저장해보려고 한다.
- 헤더 파일 (BinaryTree3.h)
#ifndef __BINARY_TREE3_H__
#define __BINARY_TREE3_H__
typedef int BTData;
typedef struct _bTreeNode
{
BTData data;
struct _bTreeNode * left;
struct _bTreeNode * right;
} BTreeNode;
BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);
BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
// 순회 방법 함수
typedef void (*VisitFuncPtr)(BTData data);
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action);
// 노드 삭제 관련 함수 추가
BTreeNode * RemoveLeftSubTree(BTreeNode * bt);
BTreeNode * RemoveRightSubTree(BTreeNode * bt);
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub);
#endif- 소스 파일 (BinaryTree3.c)
#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree3.h"
BTreeNode * MakeBTreeNode(void)
{
BTreeNode * nd = (BTreeNode *)malloc(sizeof(BTreeNode));
nd->left = NULL;
nd->right = NULL;
return nd;
}
BTData GetData(BTreeNode * bt)
{
return bt->data;
}
void SetData(BTreeNode * bt, BTData data)
{
bt->data = data;
}
BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
return bt->left;
}
BTreeNode * GetRightSubTree(BTreeNode * bt)
{
return bt->right;
}
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->left != NULL)
free(main->left);
main->left = sub;
}
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->right != NULL)
free(main->right);
main->right = sub;
}
// 중위 순회
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
InorderTraverse(bt->left, action);
action(bt->data);
InorderTraverse(bt->right, action);
}
// 후위 순회
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
PostorderTraverse(bt->left, action);
PostorderTraverse(bt->right, action);
action(bt->data);
}
// 전위 순회
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
action(bt->data);
PreorderTraverse(bt->left, action);
PreorderTraverse(bt->right, action);
}
BTreeNode * RemoveLeftSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->left;
bt->left = NULL;
}
return delNode;
}
BTreeNode * RemoveRightSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->right;
bt->right = NULL;
}
return delNode;
}
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
main->left = sub;
}
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
main->right = sub;
}[4] 삭제 3 : 완전한 구현
삭제 기능을 추가한 이진 탐색 트리의 완전한 구현결과를 보기 위해서 다음 두 개의 파일을 작성하자.
- BinarySearchTree2.h : 이진 탐색 트리의 헤더파일
- BinarySearchTree2.c : 이진 탐색 트리의 소스파일
이전에 구현한 이진 탐색 트리(BinarySearchTree.h, BinarySearchTree.c)의 확장판이다.
- 헤더 파일 (BinarySearchTree2.h)
#ifndef __BINARY_SEARCH_TREE2_H__
#define __BINARY_SEARCH_TREE2_H__
#include "BinaryTree3.h"
typedef BTData BSTData;
// BST의 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot);
// 노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode * bst);
// BST를 대상으로 데이터 저장(노드의 생성과정 포함)
void BSTInsert(BTreeNode ** pRoot, BSTData data);
// BST를 대상으로 데이터 탐색
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target);
// ㅌ리에서 노드를 제거하고 제거된 노드의 주소 값 반환
BTreeNode * BSTRemove(BTreeNode ** pRoot, BSTData target);
// 이진 탐색 트리에 저장된 모든 노드의 데이터 출력
void BSTShowAll(BTreeNode * bst);
#endif- 소스 파일 (BinarySearchTree2.c)
거의 BinarySearchTree.c 함수와 동일하고 마지막 함수 3개만 추가되었다.
#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree3.h"
#include "BinarySearchTree2.h"
void BSTMakeAndInit(BTreeNode ** pRoot)
{
*pRoot = NULL;
}
BSTData BSTGetNodeData(BTreeNode * bst)
{
return GetData(bst);
}
void BSTInsert(BTreeNode ** pRoot, BSTData data)
{
BTreeNode * pNode = NULL; // parent node
BTreeNode * cNode = *pRoot; // current node
BTreeNode * nNode = NULL; // new node
// 새로운 노드(새 데이터 담긴 노드)가 추가될 위치 찾기
while(cNode != NULL)
{
if(data == GetData(cNode))
return; // already inserted
pNode = cNode;
if(GetData(cNode) > data)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
// pNode의 자식 노드로 추가할 새 노드의 생성
nNode = MakeBTreeNode(); // 새 노드 생성
SetData(nNode, data); // 새 노드에 데이터 저장
// pNode의 자식 노드로 새 노드를 추가
if(pNode != NULL) // 새 노드가 루트 노드가 아니라면
{
if(data < GetData(pNode))
MakeLeftSubTree(pNode, nNode);
else
MakeRightSubTree(pNode, nNode);
}
else // 새 노드가 루트 노드라면
{
*pRoot = nNode;
}
}
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target)
{
BTreeNode * cNode = bst; // current node
BSTData cd; // current data
while(cNode != NULL)
{
cd = GetData(cNode);
if(target == cd)
return cNode;
else if(target < cd)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
return NULL; // 탐색대상이 저장되어 있지 않음.
}
BTreeNode * BSTRemove(BTreeNode ** pRoot, BSTData target)
{
// 삭제 대상이 루트 노드인 경우 별도로 고려
BTreeNode * pVRoot = MakeBTreeNode(); // 가상의 루트 노드
BTreeNode * pNode = pVRoot; // parent node
BTreeNode * cNode = *pRoot; // current node
BTreeNode * dNode; // delete node
// 루트 노드를 pVRoot가 가리키는 노드의 오른쪽 자식 노드가 되게
ChangeRightSubTree(pVRoot, *pRoot);
// 삭제 대상인 노드를 탐색
while(cNode != NULL && GetData(cNode) != target)
{
pNode = cNode;
if(target < GetData(cNode))
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
// 삭제 대상이 존재하지 않다면
if(cNode == NULL)
return NULL;
// 삭제 대상 dNode 가리키게
dNode = cNode;
// 경우 1) 삭제 대상이 단말 노드
if(GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode) == NULL)
{
if(GetLeftSubTree(pNode) == dNode)
RemoveLeftSubTree(pNode);
else
RemoveRightSubTree(pNode);
}
// 경우 2) 삭제 대상이 하나의 자식 노드
else if(GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode) == NULL)
{
// 삭제 대상의 자식 노드
BTreeNode * dcNode;
if(GetLeftSubTree(dNode) != NULL)
dcNode = GetLeftSubTree(dNode);
else
dcNode = GetRightSubTree(dNode);
if(GetLeftSubTree(pNode) == dNode)
ChangeLeftSubTree(pNode, dcNode);
else
ChangeRightSubTree(pNode, dcNode);
}
// 경우 3) 삭제 대상이 두 개의 자식 노드
else
{
// 대체 노드 가리킴
BTreeNode * mNode = GetRightSubTree(dNode);
// 대체 노드의 부모 노드
BTreeNode * mpNode = dNode;
int delData;
// 삭제 대상의 대체 노드 찾기
while(GetLeftSubTree(mNode) != NULL)
{
mpNode = mNode;
mNode = GetLeftSubTree(mNode);
}
// 대체 노드에 저장된 값을 삭제 노드에 대입
delData = GetData(dNode);
SetData(dNode, GetData(mNode));
// 대체 노드의 부모 노드와 자식 노드 연결
if(GetLeftSubTree(mpNode) == mNode)
ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
else
ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
dNode = mNode;
SetData(dNode, delData);
}
// 삭제된 노드가 루트 노드인 경우
if(GetRightSubTree(pVRoot) != *pRoot)
*pRoot = GetRightSubTree(pVRoot); // 루트 노드의 변경 반영
free(pVRoot); // 가상 루트 노드 소멸
return dNode; // 삭제된 노드 반환
}
void ShowIntData(int data)
{
printf("%d ", data);
}
void BSTShowAll(BTreeNode * bst)
{
// 중위 순회
InorderTraverse(bst, ShowIntData);
printf("\n");
}위 함수 중 BSTRemove 함수에 대한 이해를 돕기 위해 그림을 하나 살펴보자.
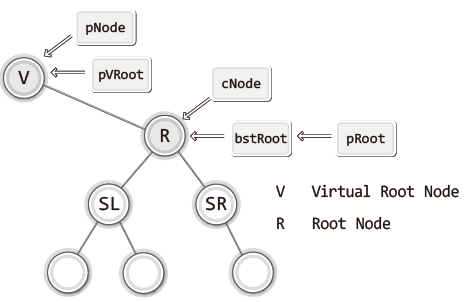
V라는 노드를 하나 생성해서 실제 루트 노드인 R이 V의 오른쪽 자식 노드가 되게 한다.
이는 삭제할 노드가 루트 노드인 경우의 예외적인 삭제흐름을 일반화 하기 위함이다.
루트 노드를 삭제할 경우 코드에서는 cNode와 pNode가 연결되어 있어 삭제할 때 부모와 자식을 연결시키는 가정이 있기 때문에 cNode의 부모 노드를 언제든 가리키고 있어야 한다.
따라서 V라는 가상의 노드를 만들어 부모 노드와 자식 노드의 연결을 만들어주는 것이다.
(과정을 일반화 하기 위함)
그리고 삭제 대상을 탐색하기 위해서 while문을 사용했는데 BSTSearch 함수를 사용하지 않은 이유는 반복문을 실행하게 되면 cNode는 삭제할 노드를 가리키게 되는데, BSTSearch 함수를 사용하면 cNode의 부모 노드를 pNode가 가리킬 수 없게 되기 때문이다.
따라서 pNode가 가리키는 대상의 갱신을 위해서 별도의 반복문을 구성한 것이다.
마지막으로, 이진 탐색 트리를 대상으로 중위 순회를 할 경우 정렬된 순서대로 데이터를 참조 및 출력할 수 있다.
- 실행 파일 (BinarySearchTreeDelMain.c)
#include <stdio.h>
#include <stdlib.h>
#include "BinarySearchTree2.h"
int main()
{
BTreeNode * bstRoot;
BTreeNode * sNode;
BSTMakeAndInit(&bstRoot);
BSTInsert(&bstRoot, 5);
BSTInsert(&bstRoot, 8);
BSTInsert(&bstRoot, 1);
BSTInsert(&bstRoot, 6);
BSTInsert(&bstRoot, 4);
BSTInsert(&bstRoot, 9);
BSTInsert(&bstRoot, 3);
BSTInsert(&bstRoot, 2);
BSTInsert(&bstRoot, 7);
BSTShowAll(bstRoot);
sNode = BSTRemove(&bstRoot, 3);
free(sNode);
BSTShowAll(bstRoot);
sNode = BSTRemove(&bstRoot, 8);
free(sNode);
BSTShowAll(bstRoot);
sNode = BSTRemove(&bstRoot, 1);
free(sNode);
BSTShowAll(bstRoot);
sNode = BSTRemove(&bstRoot, 6);
free(sNode);
BSTShowAll(bstRoot);
return 0;
}
> gcc .\BinarySearchTree2.c .\BinarySerachTreeDelMain.c .\BinaryTree3.c > .\a.exe
> 출력
1 2 3 4 5 6 7 8 9
1 2 4 5 6 7 8 9
1 2 4 5 6 7 9
2 4 5 6 7 9
2 4 5 7 9<Review>
탐색에 대한 부분이 절반 정도 끝이 났다.
사실 마지막 이진 탐색 트리의 삭제에 대한 부분은 아직도 이해가 잘 안가서 그림을 그리면서 다시 복습해봐야겠다.
(어차피 삭제되도 오른쪽 자식을 가져온다는 부분이 이해가 안된달까....)
그래도 여기까지 온 내 자신이 대견하다...!
앞으로 chapter 3개가 남았는데 그 때까지 화이팅!!


