Chapter 08. 트리(Tree)

김민정·2024년 11월 4일

c언어 tree 개발 기술블로그 코딩 트리

윤성우 열혈 자료구조

목록 보기

8/14

08-1. 트리의 개요

이번에 배우게 될 트리(Tree)는 고급 자료구조로 구분된다.
이전에 배운 선형 자료구조들과 달리 트리는 비선형 자료구조다.
집중해서 알아보자~!

트리(Tree)의 접근

트리(Tree)는 계층적 관계(Hierarchical Relationship)를 표현하는 자료구조다.
이번에 배울 트리는 '계층적 관계'라는 점도 중요하지만 '표현'하는 자료구조라는 점도 매우 중요하다.
데이터의 저장과 삭제가 아닌 '표현'에 초점이 맞춰서 트리에 대해 배울 것이기 때문에 이 점을 꼭 기억하면서 학습하면 좋다.
따라서 트리의 ADT를 정의하거나 배울 때 "트리의 구조로 이뤄진 무엇인가를 표현하기에 적절히 정의되어 있나?"를 생각하며 트리를 표현하는 것이 좋다.

트리가 표현할 수 있는 것들

그렇다면 트리는 무엇을 표현하기 위한 자료구조일까?
사실 트리도 큐와 비슷하게 주변에서 쉽게 찾아 볼 수 있는 자료구조다.
컴퓨터의 디렉터리 구조, 집안의 족보, 기업 및 정부의 조직도도 트리의 예시다.

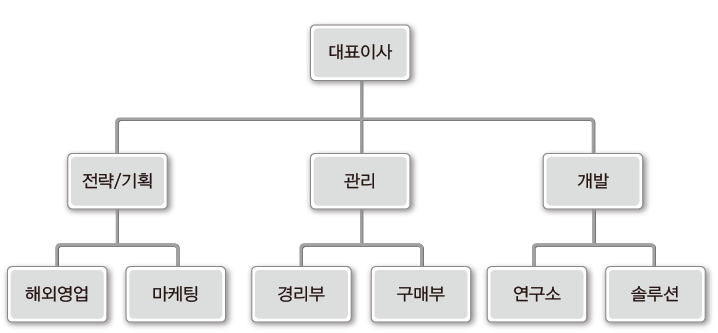
따라서 트리 구조라는 것은 나무처럼 가지를 늘려가며 뻗어나가는 것이다.
트리는 어떠한 데이터를 저장하고 꺼내서 사용하는 것이 아닌 무엇인가를 대표하는 도구라 생각하고 학습하면 편하다~!

트리 관련 용어

트리와 관련해서 많은 용어가 정의되어 있다.

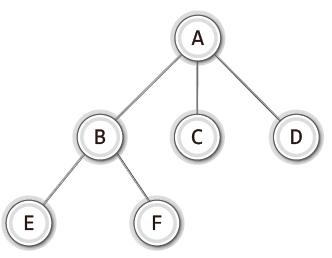
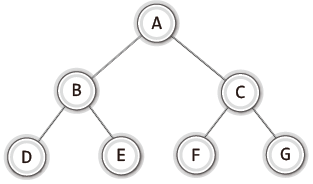
노드(node)
: 트리의 구성요소에 해당하는 A, B, C, D, E, F와 같은 요소
간선(edge)
: 노드와 노드를 연결하는 연결선
루트 노드(root node)
: 트리 구조에서 최상위에 존재하는 A와 같은 노드
단말 노드(terminal node)_입사귀 노드(leaf node)
: 아래로 또 다른 노드가 연결되어 있지 않은 E, F, C, D와 같은 요소
내부 노드(internal node)_비단말 노드(nonterminal node)
: 단말 노드를 제외한 모든 노드로 A, B와 같은 노드

트리 내 노드간에는 부모(parent), 자식(child), 형제(sibling)의 관계가 성립되어 다음과 같은 표현도 할 수 있다.
(참고로 트리의 구조상 위에 있을수록 촌수가 높다.)

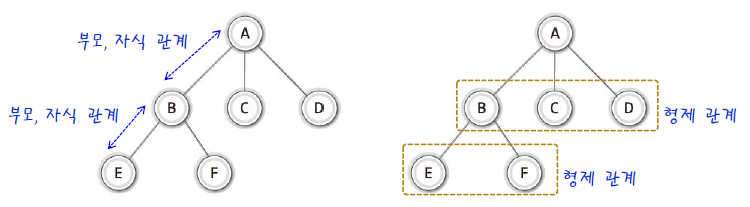
노드 A는 노드 B, C, D의 부모 노드(parent node)다.
노드 B, C, D는 노드 A의 자식 노드(child node)다.
노드 B, C, D는 부모 노드가 같으므로 서로가 서로에게 형제 노드(sibling node)다.

부모와 자식의 관계는 상대적이므로 노드 B는 노드 A에게 자식 노드이면서 노드 E와 F의 부모 노드도 된다.

조금 더 확장해서 조상(Ancestor)과 후손(Descendant)의 관계도 있다.
특정 노드의 위에 위치한 모든 노드를 가리며 조상 노드라 하고,
특정 노드의 아래에 위치한 모든 노드를 가리켜 후손 노드라 한다.
즉, 노드 A와 B는 노드 E의 조상 노드고 B, C, D, E, F는 모두 노드 A의 후손 노드다.

트리에서는 각 층별로 숫자를 매겨서 이를 트리의 '레벨(level)'이라 하고 트리의 최고 레벨을 가리켜 '높이(height)'라 한다.

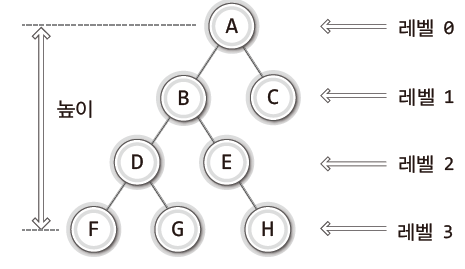
그림과 같이 트리는 레벨 0부터 시작해 최종 레벨이 3이고 이것이 트리의 높이가 된다.

트리의 종류

1) 서브 트리 (Sub Tree)

큰 트리는 작은 트리들로 구성되어 있다.
큰 트리에 속하는 작은 트리를 가리켜 '서브 트리(sub tree)'라 한다.

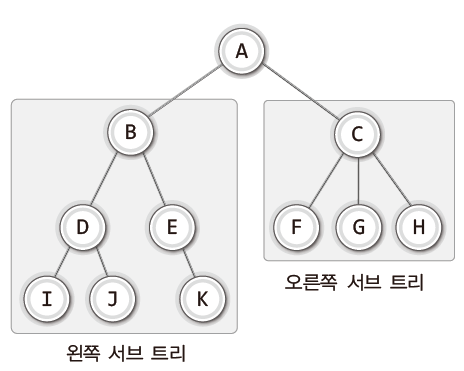
큰 트리 안에 노드 B를 루트 노드로 하는 서브 트리가 있다.
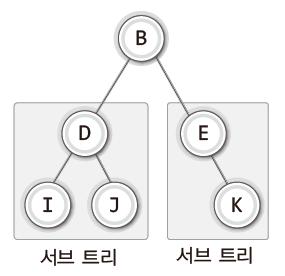
이 트리 안에도 노드 D를 루트 노드로 하는 서브 트리와 노드 E를 루트 노드로 하는 서브 트리가 있다.

2) 이진 트리 (Binary Tree)

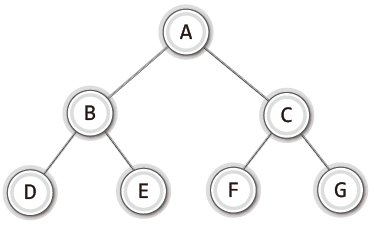
트리 중에서도 이진 트리(Binary Tree)라는 것이 있는데 이진 트리에 해당하기 위한 조건은 다음 두 가지와 같다.

루트 노드를 중심으로 두 개의 서브 트리로 나눠진다.
나눠진 두 서브 트리도 모두 이진 트리여야 한다.

정의 안에 이진 트리라는 단어가 들어가 있으므로 재귀적인 느낌을 받을 수 있다.
만약에 아래와 같은 트리가 있다면 이것은 이진 트리가 아닐까?

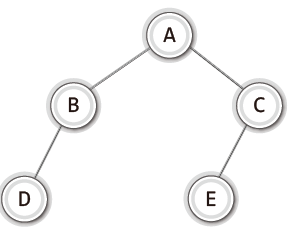
이것도 이진 트리가 맞다.
이진 트리를 정의할 땐 노드가 위치할 수 있는 곳에 노드가 존재하지 않을 경우 공집합(empty set) 노드가 존재하는 것으로 간주하기 때문이다.

따라서 이진 트리에서 말하는 공집합 노드를 추가해주면 아래와 같이 표현할 수 있다.

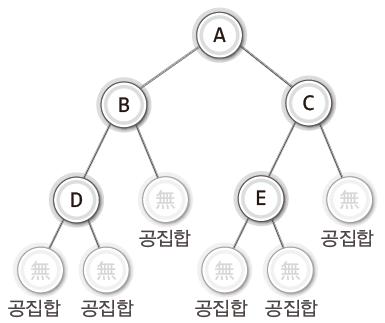
이러한 공집합 노드 덕분에 서브트리가 하나인 노드 B와 C도 그리고 단말 노드인 D와 E도 모두 이진 트리가 될 수 있다.

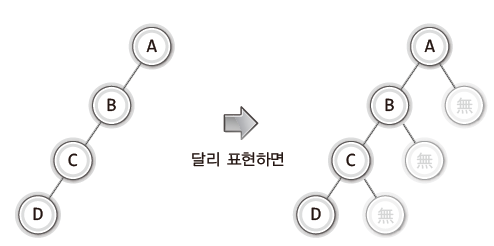
한줄로 되어있는 트리도 공집합을 넣어주면 이진 트리가 될 수 있다.

3) 포화 이진 트리 (Full Binary Tree)

위 그림과 같이 모든 레벨이 꽉 찬 이진 트리를 가리켜 '포화 이진 트리(Full Binary Tree)'라 한다.

4) 완전 이진 트리 (Complete Binary Tree)

위에서 예시를 든 포화 이진 트리에서 레벨을 하나 더 늘려서 노드 H와 I를 추가한 트리가 있다.

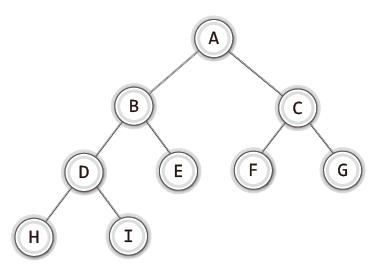
위 트리를 가리켜 '완전 이진 트리(Complete Binary Tree)'라 한다.
포화 이진 트리처럼 모든 레벨이 꽉 찬 상태는 아니지만 차곡차곡 빈 틈 없이 노드가 채워진 이진 트리를 말한다.
여기서 '차곡차곡 빈 틈 없이 채워졌다'라는 것은 "노드가 위에서 아래로, 그리고 왼쪽에서 오른쪽의 순서대로 채워졌다."라는 의미다.

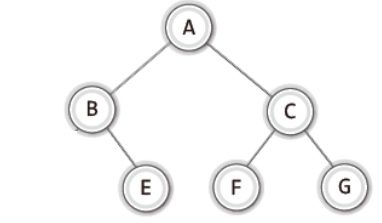
완전 이진 트리와 달리 그냥 이진 트리는 다음과 같은 구조를 말한다.

08-2. 이진 트리의 구현

트리에 대한 기본적인 것을 배웠으니 이제 트리 구현에 대해 배워보자!
이진 트리는 재귀적인 특성을 가지고 있다.
이러한 특성 때문에 이진 트리와 관련된 일부 연산은 재귀호출의 형태를 띈다.

배열 기반 구현 or 연결 리스트 기반 구현

이진 트리 역시 배열 기반으로도, 연결 리스트 기반으로도 구현이 가능하다.
하지만 트리를 표현하기에는 연결 리스트가 더 유연하기 때문에 연결 리스트 기반으로 구현하는 방법으로 배울 것이다.
단, 트리가 완성 된 이후부터 트리를 대상으로 매우 빈번하게 탐색이 이뤄지는 완전 이진 트리의 경우 배열 기반의 구현이 좀 더 용이하고 빠르다.
그 이유는 배열이 연결 리스트에 비해 탐색에 있어 매우 용이하고 빠르기 때문이다.
따라서 배열 기반으로 이진 트리를 구성하는 방법에 대해 간단하게 알아보고,
대부분의 학습을 연결 기반의 이진 트리 구현으로 할 것이다.

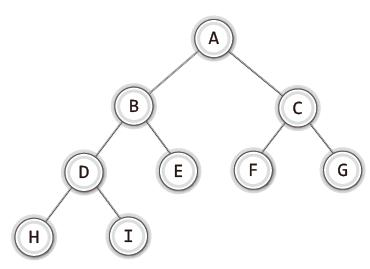
다음과 같이 이진 트리가 있다고 가정해보자.
이 이진 트리를 배열 기반으로 구현하려면 각 노드에 번호를 부여해야한다.
이 번호는 각 노드의 ㄷ이터가 저장되어야할 배열의 인덱스 값을 의미하게 된다.

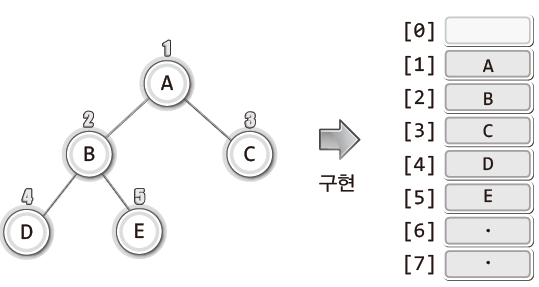
길이가 8인 배열을 선언하여 노드 번호 1부터 5까지의 노드에 저장된 데이터를 배열에 저장했다.
데이터가 저장되는 배열의 위치는 노드 번호 기준으로 결정되었다.

그렇다면 연결 리스트 기반으로 트리를 어떻게 구현할 수 있을까?

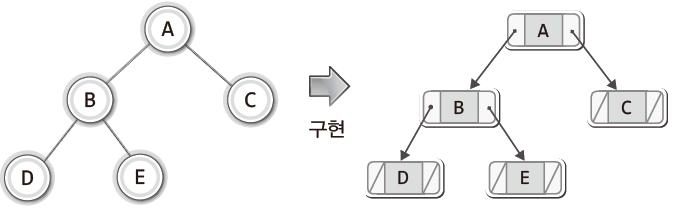
연결 리스트 기반으로 트리를 구현한다면 연결 리스트이 구성 형태가 실제 트리와 일치하기 때문에 용이하다~!

그렇다면 배열 기반 리스트는 사용하지 않을까?
아니다. 완전 이진 트리의 구조를 갖는 '힙(heap)'이라는 자료구조는 배열을 기반으로 구현하기 때문에 배열 기반의 트리와 연결 리스트 기반의 트리 모두 중요하다.
(힙은 다음 chapter에서 배울 예정이다.)

1) 헤더파일 정의

원래는 ADT를 정의한 다음에 헤더 파일을 정의한 다음 ADT를 정의하려한다.
ADT를 먼저 정의할 경우 이해하기 어려운 부분이 있기 때문이다.
연결리스트 기반의 트리 구현에서 헤더 파일은 다음과 같다.

// BinaryTree.h
#ifndef __BINARY_TREE_H__
#define __BINARY_TREE_H__

typedef int BTData;

typedef struct _bTreeNode
{
    BTData data;
    struct _bTreeNode * left;
    struct _bTreeNode * right;
} BTreeNode;

BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);

BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);

#endif

헤더파일에 정의되어 있는 구조체는 다음과 같다.

typedef struct _bTreeNode	// 이진 트리의 노드를 표현한 구조체
{
	BTData data;
    struct _bTreeNode * left;
    struct _bTreeNode * right;
} BTreeNode;

이진 트리를 표현하기 위함인데 노드의 구조체만 정의되어 있고 이진 트리를 표현한 구조체는 없다.
이는 노드가 위치할 수 있는 곳에 노드가 존재하지 않는다면 공집합(empty set) 노드가 존재하는 것으로 간주하고 공집합 노드도 이진 트리를 판단하는데 있어서 노드로 인정하기 때문이다.

위 그림과 같이 하나의 노드는 두 개의 공집합 노드를 자식으로 두고 있는 그 자체로도 이진 트리이다.
그러므로 구조체 BTreeNode는 노드를 표현함과 동시에 이진 트리를 표현한 결과가 된다.
구조체 포인터 변수의 이름은 BTreeNode * pnode;로 선언될 수 있지만, 어떻게 보면 BTreeNode * ptree;로 선언되는 것과 같은 것이다.
(이 문장의 의미는 BTreeNode는 노드의 표현 결과뿐만 아니라 이진 트리의 표현 결과도 된다는 것이다.)

2) 이진 트리 ADT 정의

위에서 정의한 헤더파일을 바탕으로 이진 트리의 구현 및 연산에 대해 생각해보자.
중요한 점은 이진 트리의 재귀적인 성향을 이해하는 것이다.

헤더파일에서 이진 트리를 만드는 도구가 되는 함수 3가지가 있다.

BTreeNode * MakeBTreeNode(void); : 노드의 생성
BTData GetData(BTreeNode * bt); : 노드에 저장된 데이터 반환
void SetData(BTreeNode * bt, BTData data); : 노드에 데이터 저장

여기서 노드의 생성을 담당하는 MakeBTreeNode함수는 호출되면 다음 그림과 같은 형태의 노드를 동적 할당 및 초기화하여 그 주소값을 반환한다.

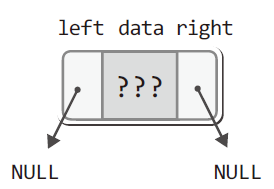
위 물음표는 데이터가 저장되는 부분이며 첫 초기화에서는 데이터가 저장되는 멤버 data를 대상으로 별도의 초기화를 진행하지 않는다.
그러나 왼쪽 서브 트리와 오른쪽 서브 트리를 가리키기 위한 멤버 left와 right은 NULL로 초괴화한다.

그 다음 왼쪽과 오른쪽 서브 트리의 주소 값을 반환하는 함수 2가지가 있다.

BTreeNode * GetLeftSubTree(BTreeNode * bt); : 왼쪽 서브 트리 주소 값 반환
BTreeNode * GetRightSubTree(BTreeNode * bt); : 오른쪽 서브 트리 주소 값 반환

루트 노드를 포함하여 어떠한 노드의 주소 값도 위 함수의 인자로 전달될 수 있다.
두 함수는 각각 인자로 전달된 이진 트리의 왼쪽 서브 트리, 오른쪽 서브 트리의 루트 노드의 주소 값(또는 그냥 노드의 주소 값)을 반환하는 함수다.

그리고 마지막으로 함수 2가지가 더 정의되어 있다.

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);

위 두 함수는 서브 트리의 연결을 담당한다.
첫 번째 함수는 매개 변수 sub으로 전달된 트리 또는 노드를 매개변수 main으로 전달된 노드의 왼쪽 서브 트리로 연결한다.
두 번째 함수는 마찬가지로 전달된 노드를 오른쪽 서브 트리로 연결한다.
이 두 함수는 연결을 담당할 뿐, 노드나 트리의 생성을 담당하지 않는다.

위 함수들의 역할을 이해하기 위해 예시를 보자.
"만약 노드 A, B, C를 생성해서 A를 루트로 하고 B와 C를 각각 A의 왼쪽과 오른쪽 자식 노드가 되도록 하려면 함수의 호출 흐름을 어떻게 하면 좋을까?"
순서는 다음가 같이 구성할 수 있다.

int main()
{
	BTreeNode * ndA = MakeBTreeNode();	// 노드 A 생성
    BTreeNode * ndB = MakeBTreeNode();	// 노드 B 생성
    BTreeNode * ndC = MakeBTreeNode();	// 노드 C 생성
    ....
    MakeLeftSubTree(ndA, ndB);	// 노드 A의 왼쪽 자식 노드로 노드 B 연결
    MakeRightSubTree(ndA, ndC);	// 노드 A의 오른쪽 자식 노드로 노드 C 연결
    ....
}

하나의 노드는 곧 하나의 이진 트리와 같다고 앞서 배웠기 때문에 노드를 루트노드에 연결할 때도 MakeLeft(Right)SubTree함수가 사용된다.

위에서 설명한 내용을 ADT 정의로 정리해보자.

✅Operations:

BTreeNode * MakeBRTreeNode(void);
- 이진 트리 노드를 생성하여 그 주소 값 반환
BTData GetData(BTreeNode * bt);
- 노드에 저장된 데이터를 반환
void SetData(BTreeNode * bt, BTData data);
- 노드에 데이터 저장. data로 전달된 값 저장
BTreeNode GetLeftSubTree(BTreeNode bt);
- 왼쪽 서브 트리의 주소 값을 반환
BTreeNode GetRightSubTree(BTreeNode bt);
- 오른쪽 서브 트리의 주소 값을 반환
void MakeLeftSubTree(BTreeNode main, BTreeNode sub);
- 왼쪽 서브 트리를 연결
void MakeRightSubTree(BTreeNode main, BTreeNode sub);
- 오른쪽 서브 트리를 연결

3) 소스파일 정의

위에서 정의한 ADT와 헤더파일을 바탕으로 소스파일을 정의해보자.

#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree.h"

BTreeNode * MakeBTreeNode(void)
{
    BTreeNode * nd = (BTreeNode *)malloc(sizeof(BTreeNode));
    nd->left = NULL;
    nd->right = NULL;
    return nd;
}

BTData GetData(BTreeNode * bt)
{
    return bt->data;
}

void SetData(BTreeNode * bt, BTData data)
{
    bt->data = data;
}

BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
    return bt->left;
}

BTreeNode * GetRightSubTree(BTreeNode * bt)
{
    return bt->right;
}

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main->left != NULL)
        free(main->left);

    main->left = sub;
}

void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main->right != NULL)
        free(main->right);
    
    main->right = sub;
}

여기서 MakeLeftSubTree와 MakeRightSubTree를 좀 더 살펴보자.
왼쪽 또는 오른쪽 서브 트리가 존재한다면, 해당 트리를 삭제하고 새로운 왼쪽 또는 오른쪽 서브 트리를 연결한다.
이는 함수 구현에 있어서 나름 의미를 부여할 수 있는 선택이다.
하지만 free 함수 호출이 한번만 이뤄지기 때문에 삭제할 서브 트리가 하나의 노드로 이뤄져 있다면 문제되지 않지만 그렇지 않다면 메모리 누수가 발생하게 된다.
따라서 둘 이상의 노드로 이뤄져 있는 서브 트리를 완전히 삭제하려면 서브 트리를 구성하는 모든 노드를 대상으로 free 함수를 호출해야한다.
모든 노드의 방문이 필요한 것이다.
이렇게 모든 노드를 방문하는 것을 '순회'라 하고 이진 트리의 순회는 연결 리스트의 순회와 달리 별도의 방법이 필요하다.
우선 이진 트리 구성의 예를 보이는 실행파일을 정의하고
이후에 순회에 대한 여러 방법에 대해 배워보자.

4) 실행파일 정의

#include <stdio.h>
#include "BinaryTree.h"

int main()
{
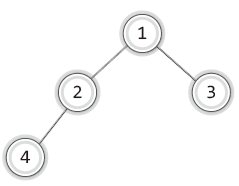
    BTreeNode * bt1 = MakeBTreeNode();     // 노드 bt1 생성
    BTreeNode * bt2 = MakeBTreeNode();     // 노드 bt2 생성
    BTreeNode * bt3 = MakeBTreeNode();     // 노드 bt3 생성
    BTreeNode * bt4 = MakeBTreeNode();     // 노드 bt4 생성

    SetData(bt1, 1);    // bt1에 1 저장
    SetData(bt2, 2);    // bt2에 2 저장
    SetData(bt3, 3);    // bt3에 3 저장
    SetData(bt4, 4);    // bt4에 4 저장

    MakeLeftSubTree(bt1, bt2);    // bt1의 왼쪽 자식 노드 bt2로 설정
    MakeRightSubTree(bt1, bt3);   // bt1의 오른쪽 자식 노드 bt3으로 설정
    MakeLeftSubTree(bt2, bt4);    // bt2의 왼쪽 자식 노드 bt4로 설정

    printf("bt1의 왼쪽 자식 노드의 데이터 출력\n");
    printf("%d \n", GetData(GetLeftSubTree(bt1)));

    printf("bt1의 왼쪽 자식 노드의 왼쪽 자식 노드의 데이터 출력\n");
    printf("%d \n", GetData(GetLeftSubTree(GetLeftSubTree(bt1))));

    return 0;
}

> gcc .\BinaryTree.c .\BinaryTreeMain.c
> .\a.exe   
> 출력
bt1의 왼쪽 자식 노드의 데이터 출력
2
bt1의 왼쪽 자식 노드의 왼쪽 자식 노드의 데이터 출력
4

위 실행파일을 통해 형성되는 이진 트리의 구조는 다음 그림과 같다.

08-3. 이진 트리의 순회(Traversal)

이진 트리의 순회가 필요한 부분은 앞에서 언급했다.
트리의 순회 방법은 총 3가지 있고 순회 방법 또한 재귀적이다.

순회 방법

중위 순회(Inorder Traversal) : 루트 노드를 중간에
후위 순회(Postorder Traversal) : 루트 노드를 마지막에
전위 순회(Preorder Traversal) : 루트 노드 먼저

루트 노드를 언제 방문하느냐에 따라 순회 방법은 3가지로 나뉜다.

다음 그림과 같은 순서 및 방향으로 순회할 경우 루트 노드는 중간에 방문하기 때문에 이러한 방식의 순회를 가리켜 '중위 순회'라 한다.

다음 그림과 같은 순서 및 방향으로 순회할 경우 루트 노드를 마지막에 방문하므로 이러한 방식의 순회를 가리켜 '후위 순회'라 한다.

다음 그림과 같은 순서 및 방향으로 순회할 경우 루트 노드를 가장 먼저 방문하기 때문에 이러한 방식의 순회를 가리켜 '전위 순회'라 한다.

순회 방법은 루트 노드와 이를 부모로 하는 두 자식 노드를 놓고 한쪽 방향으로 순서대로 방문하면 된다.

그럼 높이가 2 이상인 이진 트리는 어떻게 순회할까?
재귀적인 형태로 순회의 과정을 구성하면 높이에 상관없이 순회가 가능하다.

순회의 재귀적 표현

그럼 가장 먼저 중위 순회에 대한 함수를 정의해보자.
예시 이진 트리는 다음 그림과 같다.

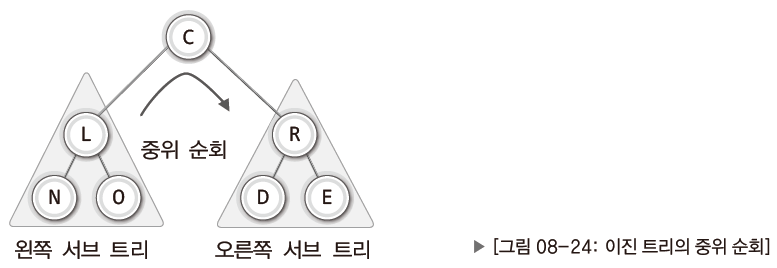
이 이진 트리를 대상으로 중위 순회를 할 경우 순회의 순서는 다음과 같다.

왼쪽 서브 트리의 순회
루트 노드의 방문
오른쪽 서브 트리의 순회

여기서 주목해야하는 순서는 1번, 3번이다.
각 서브 트리도 정한 순회 방법(중위 순회)으로 순회를 진행하면 된다.
따라서 이진 트리 전체를 중위 순회 하는 함수는 개략적으로 다음과 같이 정의할 수 있다.

void InorderTraverse(BTreeNode * bt)
{
	InorderTraverse(bt->left);		// 1. 왼쪽 서브 트리의 순회
    printf("%d \n", bt->data);		// 2. 루트 노드 방문
    InorderTraverse(bt->right);		// 3. 오른쪽 서브 트리의 순회
}

위 함수에 대해 다음과 같은 의문이 들 수 있다.
"재귀의 탈출 조건은 무엇인가?", "노드의 방문이 그저 데이터 출력인가?"
노드에 저장된 데이터의 출력으로 노드의 방문이 이뤄진 것으로 가정한 이유는
순회 방법에 초점을 두기 위함이다.
재귀의 탈출 조건에 관해서 다음 이진 트리를 예시로 이해해보자.

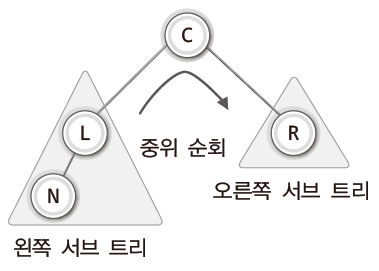
루트 노드가 L인 왼쪽 서브 트리에서는 다음의 과정을 거쳐서 순회를 진행하게 된다.

왼쪽 서브 트리의 순회 (노드 N 대상)
루트 노드의 방문 (노드 L 대상)
오른쪽 서브 트리의 순회 (공집합 노드 대상)

여기 3번 순서에서 노드 L의 오른쪽 서브 트리가 NULL이므로 함수에 NULL이 전달되기 때문에 재귀의 탈출 조건이 성립된다.
따라서 함수는 다음과 같이 정의되어야 한다.

void InorderTraverse(BTreeNode * bt)
{
	if(bt == NULL)	// bt가 NULL이면 재귀 탈출
    	return;
        
    InorderTraverse(bt->left);
    printf("%d \n", bt->data);
    InorderTraverse(bt->right);
}

위에서 배운 중위순회를 실행파일로 만들어서 확인해보자.
(이전에 정의한 헤더파일과 소스파일을 사용한다.)

#include <stdio.h>
#include "BinaryTree.h"

void InorderTraverse(BTreeNode * bt)
{
    if(bt == NULL)  // bt가 NULL이면 재귀 탈출
        return;

    InorderTraverse(bt->left);
    printf("%d \n", bt->data);
    InorderTraverse(bt->right);
}

int main()
{
    BTreeNode * bt1 = MakeBTreeNode();
    BTreeNode * bt2 = MakeBTreeNode();
    BTreeNode * bt3 = MakeBTreeNode();
    BTreeNode * bt4 = MakeBTreeNode();

    SetData(bt1, 1);
    SetData(bt2, 2);
    SetData(bt3, 3);
    SetData(bt4, 4);

    MakeLeftSubTree(bt1, bt2);
    MakeRightSubTree(bt1, bt3);
    MakeLeftSubTree(bt2, bt4);

    printf("<Inorder Traversal Check>\n");
    InorderTraverse(bt1);
    
    return 0;
}

> gcc .\BinaryTree.c .\BinaryTreeTraverseMain.c
> .\a.exe
> 출력
<Inorder Traversal Check>
4 
2 
1
3

중위 순회와 마찬가지로 후위 순회와 전위 순회도 비슷한 방식으로 함수를 정의할 수 있다.
함수는 다음과 같다.

// 후위 순회 (Postorder Traversal)
void PostorderTraverse(BTreeNode * bt)
{
    if(bt == NULL)
        return;
    
    PostorderTraverse(bt->left);
    PostorderTraverse(bt->right);
    printf("%d \n", bt->data);  // 후위 순회로 루트 노드 마지막 방문
}

// 전위 순회 (Preorder Traversal)
void PreorderTraverse(BTreeNode * bt)
{
    if(bt == NULL)
        return;
    
    printf("%d \n", bt->data);  // 전위 순회로 루트 노드 먼저 방문
    PreorderTraverse(bt->left);
    PreorderTraverse(bt->right);
}

노드의 방문 이유

노드의 방문목적은 데이터의 출력이 전부가 아니다.
방문 목적은 상황에 따라 달라진다.
방문했을 때 할 일을 결정할 수 있도록 앞에서 정의한 순회 함수 세 가지를 약간 변경해보자.
함수 포인터를 사용할 예정이다.

// 중위 순회 함수 변경
typedef void (*VisitFuncPtr)(BTData data);

void InorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
	if(bt == NULL)
    	return;
    
    InorderTraverse(bt->left, action);
    action(bt->data);	// 노드의 방문
    InorderTraverse(bt->right, action);
}

함수의 주소 값을 매개변수 action을 통해서 전달받도록 변경했다.
따라서 매개변수 action에 전달되는 함수의 내용에 따라서 노드의 방문 결과가 결정된다.
이와 관련된 예제는 다음과 같다.

헤더파일 정의 (BinaryTree2.h)
: 앞서 정의한 헤더파일 BinaryTree.h에 중위, 후위, 전위 순회 관련 함수 선언을 추가한 것이다.

#ifndef __BINARY_TREE2_H__
#define __BINARY_TREE2_H__

typedef int BTData;

typedef struct _bTreeNode
{
    BTData data;
    struct _bTreeNode * left;
    struct _bTreeNode * right;
} BTreeNode;

BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);

BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);

// 순회 방법 함수 추가
typedef void (*VisitFuncPtr)(BTData data);

void InorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action);

#endif

소스파일 정의 (BinaryTree2.c)
: 헤더파일과 동일하게 앞서 정의한 BinaryTree.c에서 순회 관련 함수의 정의를 추가한 것이다.

#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree2.h"

BTreeNode * MakeBTreeNode(void)
{
    BTreeNode * nd = (BTreeNode *)malloc(sizeof(BTreeNode));
    nd->left = NULL;
    nd->right = NULL;
    return nd;
}

BTData GetData(BTreeNode * bt)
{
    return bt->data;
}

void SetData(BTreeNode * bt, BTData data)
{
    bt->data = data;
}

BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
    return bt->left;
}

BTreeNode * GetRightSubTree(BTreeNode * bt)
{
    return bt->right;
}

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main->left != NULL)
        free(main->left);

    main->left = sub;
}

void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main->right != NULL)
        free(main->right);

    main->right = sub;
}

// 중위 순회
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
    if(bt == NULL)
        return;

    InorderTraverse(bt->left, action);
    action(bt->data);
    InorderTraverse(bt->right, action);
}

// 후위 순회
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
    if(bt == NULL)
        return;

    PostorderTraverse(bt->left, action);
    PostorderTraverse(bt->right, action);
    action(bt->data);
}

// 전위 순회
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
    if(bt == NULL)
        return;

    action(bt->data);
    PreorderTraverse(bt->left, action);
    PreorderTraverse(bt->right, action);
}

실행파일 정의 (BinaryTree2Main.c)
: 순회 관련 함수의 두 번째 인자로 전달되어 노드 방문의 결과를 결정하는 함수는 트리를 활용해서 프로그램을 구현하는 프로그램의 몫이 되어야 한다.
그래서 그러한 의미를 반영하기 위해 main 함수가 위치한 다음 소스파일에 두 번째 인자로 전달되는 함수를 정의했다.

#include <stdio.h>
#include "BinaryTree2.h"

// 노드 방문 결과 결정하는 함수
void ShowIntData(int data);

int main()
{
    BTreeNode * bt1 = MakeBTreeNode();
    BTreeNode * bt2 = MakeBTreeNode();
    BTreeNode * bt3 = MakeBTreeNode();
    BTreeNode * bt4 = MakeBTreeNode();
    BTreeNode * bt5 = MakeBTreeNode();
    BTreeNode * bt6 = MakeBTreeNode();

    SetData(bt1, 1);
    SetData(bt2, 2);
    SetData(bt3, 3);
    SetData(bt4, 4);
    SetData(bt5, 5);
    SetData(bt6, 6);

    MakeLeftSubTree(bt1, bt2);
    MakeRightSubTree(bt1, bt3);
    MakeLeftSubTree(bt2, bt4);
    MakeRightSubTree(bt2, bt5);
    MakeRightSubTree(bt3, bt6);

    printf("<Inorder Traversal>\n");
    InorderTraverse(bt1, ShowIntData);
    printf("\n");
    printf("<Postorder Traversal>\n");
    PostorderTraverse(bt1, ShowIntData);
    printf("\n");
    printf("<Preorder Traversal>\n");
    PreorderTraverse(bt1, ShowIntData);
    printf("\n");

    return 0;
}

void ShowIntData(int data)
{
    printf("%d ", data);
}

> gcc .\BinaryTree2.c .\BinaryTree2Main.c
> .\a.exe
> 출력
<Inorder Traversal>
4 2 5 1 3 6 
<Postorder Traversal>
4 5 2 6 3 1
<Preorder Traversal>
1 2 4 5 3 6

+) 이진 트리의 소멸

지금까지 구현한 이진 트리에서 소멸 관련 함수가 정의되어 있지 않다.
따라서 이진 트리를 완전히 소멸시키는 함수를 다음과 같이 선언하고 정의했다.

// 함수 선언 및 정의
void DeleteTree(BTreeNode * bt);

// 함수 호출
int main()
{
	BTreeNode * bt1 = MakeBTreeNode();
    ....
    DeleteTree(bt1);
    ....
}

위에서 작성한 BinaryTree2.h와 BinaryTree2.c에 함수를 선언하고 정의해보자.

// BinaryTreeDelete.h - BinaryTree2.h에 아래 코드 추가
void DeleteTree(BTreeNode * bt);

// BinaryTreeDelete.c - BinaryTree2.c에 아래 코드 추가
void DeleteTree(BTreeNode * bt)
{
    if(bt == NULL)
        return;
    
    DeleteTree(bt->left);
    DeleteTree(bt->right);

    printf("Delete tree data: %d \n", bt->data);
    free(bt);
}

// BinaryTreeDeleteMain.c
#include <stdio.h>
#include "BinaryTreeDelete.h"

// 노드 방문 결과 결정하는 함수
void ShowIntData(int data);

int main()
{
    BTreeNode * bt1 = MakeBTreeNode();
    BTreeNode * bt2 = MakeBTreeNode();
    BTreeNode * bt3 = MakeBTreeNode();
    BTreeNode * bt4 = MakeBTreeNode();
    BTreeNode * bt5 = MakeBTreeNode();
    BTreeNode * bt6 = MakeBTreeNode();

    SetData(bt1, 1);
    SetData(bt2, 2);
    SetData(bt3, 3);
    SetData(bt4, 4);
    SetData(bt5, 5);
    SetData(bt6, 6);

    MakeLeftSubTree(bt1, bt2);
    MakeRightSubTree(bt1, bt3);
    MakeLeftSubTree(bt2, bt4);
    MakeRightSubTree(bt2, bt5);
    MakeRightSubTree(bt3, bt6);

    // 이진 트리 소멸
    printf("Delete Binary Tree...\n");
    DeleteTree(bt1);

    return 0;
}

void ShowIntData(int data)
{
    printf("%d ", data);
}

> gcc .\BinaryTreeDelete.c .\BinaryTreeDeleteMain.c
> .\a.exe        
> 출력
Delete Binary Tree...
Delete tree data: 4 
Delete tree data: 5
Delete tree data: 2
Delete tree data: 6
Delete tree data: 3
Delete tree data: 1

트리 전체 삭제를 위한 함수에서의 핵심은 루트 노드가 마지막에 소멸되어야하기 때문에 후위 순회의 과정을 통해 데이터를 소멸해야한다는 것이다.
그리고 bt1을 소멸하므로써 루트 노드를 삭제했으므로 전체 이진 트리가 삭제된 것을 알 수 있다.

08-4. 수식 트리(Expression Tree)의 구현

이번에는 배운 이진 트리를 가지고 도구로 활용하여 이진 트리의 일종인 '수식 트리'에 대해 알아보자.

수식 트리의 이해

이진 트리를 이용해서 수식을 표현해 놓은 것을 가리켜 '수식 트리'라 한다.
(수식 트리는 이진 트리와 구분되는 별개의 것이 아니다.)

7 + 4 * 2 - 1이라는 수식이 있다.
이러한 수식을 컴퓨터는 스스로 알아서 인식할 수 없다.

int main()
{
	int result = 0;
    result = 7 + 4 * 2 - 1;
}

위와 같은 수식을 컴파일러는 바로 우리가 아는 수식으로 인식하여 계산하지 않는다.
우리가 인식하는 방법을 결정하여 컴파일러에게 알려줘야 코드가 실행되고 결과를 도출하게 된다.
컴퓨터의 유연한 판단을 유도하는 것은 쉽지 않다.
따라서 가급적 정해진 일련의 과정을 거쳐서 수식을 인식할 수 있도록 도와야 한다.
이를 위해 수식 트리라는 것을 활용하여 컴파일러의 수식해석을 좋아지게 할 수 있다.
컴파일러의 수식 이해를 위해 수식 트리를 사용한 예시는 다음과 같다.

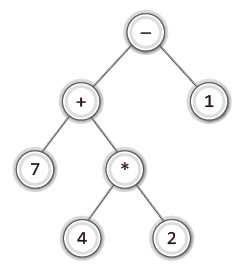
이 수식 트리를 보고 어떤 표기법을 사용하는지 궁금할 수 있다.
그런데 수식 트리는 그냥 수식 트리다.
중위 표기법이 수식 표현의 한 가지 방법이라면, 수식 트리도 수식을 표현하는 또 다른 방법일 뿐이다.
그럼 수식 트리의 계산과정은 어떻게 될까?
수식 트리를 구성하는 모든 서브 트리는 기본적으로 다음 방식으로 연산이 진행된다.
"루트 노드에 저장된 연산자의 연산을 하되, 두 개의 자식 노드에 저장된 두 피연산자를 대상으로 연산한다."

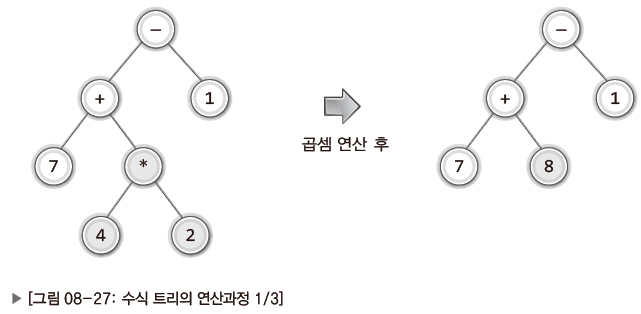
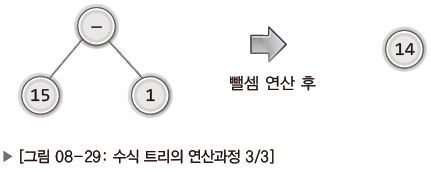
즉, 위의 수식 트리에서는 다음 그림에서 보이듯 곱셈이 먼저 진행되어 그 결과가 + 연산자의 오른쪽 자식 노드를 대체하게 된다.

그리고 이어서 + 연산이 진행되고 그 결과가 - 연산자의 왼쪽 자식 노드를 대신하게 된다.

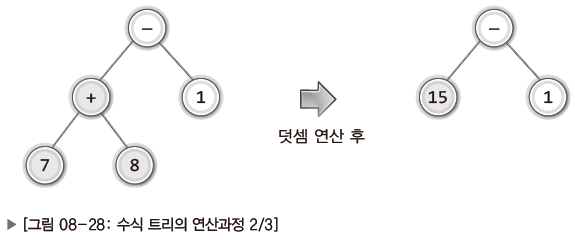
마지막으로 15와 1을 대상으로 - 연산이 진행되어 최종 연산 결과인 14를 얻게 된다.

이렇듯 수식 트리로 표현된 것을 코드로 구성하여 수식 트리를 만드는 프로그램을 만들어보자.

중위 표기법의 수식을 곧장 수식 트리로 표현하는 것은 복잡하고 힘들다.
하지만 후위 표기법 수식을 수식 트리로 표현하는 것은 비교적 간단하다.
따라서 중위 표기법의 수식 → 후위 표기법의 수식 → 수식 트리라는 과정을 거쳐서 수식 트리를 만들 것이다.
Chapter 06에서 중위 표기법의 수식을 후위 표기법의 수식으로 바꾸는 함수를 정의했었다.
따라서 이번 Chapter에서는 후위 표기법의 수식을 수식 트리로 바꾸는 것이 주가 된다.

1) 헤더파일 정의 (ExpressionTree.h)

수식 트리는 이진 트리의 한 종류기 때문에 위에서 만들어 놓은 이진 트리를 활용해서 수식 트리로 바꾸는 코드를 작성할 것이다.
수식 트리를 만드는 과정에는 스택을 필요로 한다.
(이것도 이전 Chapter에서 만들어 놓은 것을 활용하면 된다.)
따라서 프로그램 구현에 필요한 파일들은 아래와 같다.

수식 트리 구현에 필요한 이진 트리 : BinaryTree2.h, BinaryTree2.c
수식 트리 구현에 필요한 스택 : ListBaseStack.h, ListBaseStack.c

수식 트리의 표현을 위한 헤더파일은 다음과 같다.

#ifndef __EXPRESSION_TREE_H__
#define __EXPRESSION_TREE_H__

#include "BinaryTree2.h"

BTreeNode * MakeExpTree(char exp[]);        // 수식 트리 구성
int EvaluateExpTree(BTreeNode * bt);        // 수식 트리 계산

void ShowPrefixTypeExp(BTreeNode * bt);     // 전위 표기법 기반 출력
void ShowInfixTypeExp(BTreeNode * bt);      // 중위 표기법 기반 출력
void ShowPostfixTypeExp(BTreeNode * bt);    // 후위 표기법 기반 출력

#endif

위의 헤더파일에 선언된 함수 중에서 핵심이라 할 수 있는 첫 번째 함수는 다음과 같다.
(이 함수가 바로 수식 트리를 구성하는 함수다.)

BTreeNode * MakeExpTree(char exp[]);
이 함수는 후위 표기법의 수식을 문자열의 형태로 입력 받으면 이를 기반으로 수식 트리를 구성하고 수식 트리의 주소 값(수식 트리의 루트 노드의 주소 값)을 반환한다.

이어서 핵심이 되는 두 번째 함수는 인자로 전달된 수식 트리의 수식을 계산해서 그 결과를 반환하는 함수다.
int EvaluateExpTree(BTreeNode * bt);

마지막으로 수식 트리의 구성을 검증하기 위해서 각각 수식 트리의 수식을 전위, 중위, 후위 표기법으로 출력하는 기능의 함수다.
이 세 함수는 트리의 순회와 관련이 있어 그 구현이 어렵지 않다.
수식 트리를 후위 순회하면서 ㄴ드에 저장된 데이터를 출력하면 그 결과가 바로 후위 표기법의 수식이 된다.

2) 소스파일 정의 - 후위 표기법 기반 (ExpressionTree.c)

함수 MakeExpTree의 구현을 위해 후위 표기법의 수식을 수식 트리로 표현하는 방법을 알아야 한다.
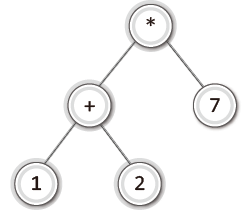
1 2 + 7 *라는 후위 표기법의 수식을 예를 들어보자.
이를 수식 트리로 표현하면 다음과 같다.

수식 트리의 구성을 위해서 후위 표기법의 다음 두 가지 특징을 알고 있어야 한다.

연산 순서대로 왼쪽에서 오른쪽으로 연산자가 나열된다.
해당 연산자의 두 피연산자는 연산자 앞에 나열된다.

그런데 수식 트리에서는 트리의 아래쪽에 위치한 연산자들의 연산이 먼저 진행된다.
때문에 후위 표기법의 수식에서 먼저 등장하는 피연산자와 연산자를 이용해서 트리의 하단을 만들고 이를 바탕으로 점진적으로 트리의 윗부분을 구성해 나가야 한다.

그렇다면 수식 트리의 구성과정에 대해 알아보자.

No.	Image	Explanation
1.		수식 트리를 만드는데 사용할 수식, 스택을 의미하는 쟁반 필요.
2.		수식을 이루는 문자를 하나씩 처리 문자가 피연산자일 경우 스택(쟁반)으로 옮기기.
3.		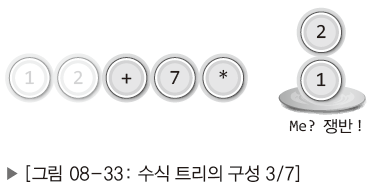두 번째 문자도 피연산자로 스택(쟁반)으로 옮기기.
4.		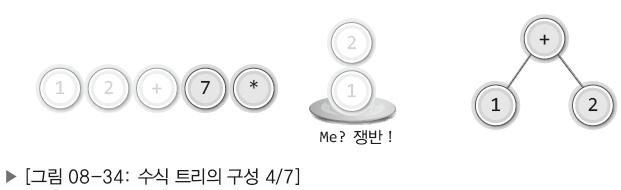연산자가 등장하면 스택에 쌓여있는 두 개의 피연산자를 꺼내어 연산자의 자식 노드로 연결. 먼저 꺼낸 피연산자가 오른쪽 자식 노드가 되고, 그 다음에 꺼낸 피연산자가 왼쪽 자식 노드가 됨.
5.		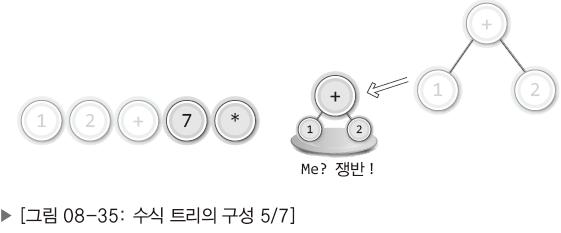만든 수식 트리 자체를 스택(쟁반)으로 옮기기.☆ 트리 전체가 다른 연산자의 자식 노드가 되기 때문. 그림으로는 트리 자체가 스택으로 옮겨지는 듯 하나 실제로는 + 연산자가 저장된 노드의 주소값만 스택으로 옮겨진다.
6.		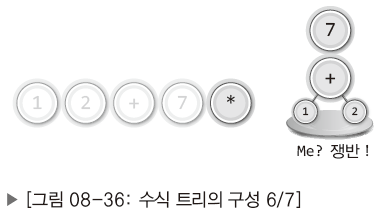피연산자를 스택(쟁반)으로 옮기기.
7.		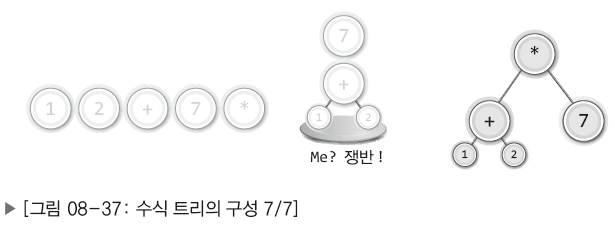최종 과정으로 연산자가 등장하면서 스택에서 두 개의 노드를 꺼내어 각각 오른쪽과 왼쪽의 자식 노드로 연결.

위 구성 과정을 정리한 수식 트리를 구성하는 방법은 다음과 같다.

피연산자를 만나면 무조건 스택으로 옮기기.
연산자를 만나면 스택에서 두 개의 피연산자를 꺼내어 자식 노드로 연결.
자식 노드를 연결해서 만들어지 늩리는 다시 스택으로 옮기기.

이 과정을 코드로 구현하면 다음과 같다.

#include "ListBaseStack.h"
#include "BinaryTree2.h"
.... 몇몇의 표준 헤더파일의 선언....

BTreeNode * MakeExpTree(char exp[])
{
	Stack stack;
    BTreeNode * pnode;
    
    int expLen = strlen(exp);
    int i;
    StackInit(&stack);
    
    for(i=0, i<expLen; i++)
    {
    	pnode = MakeBTreeNode();
        
        if(isdigit(exp[i]))		// 피연산자일 경우
        {
        	SetData(pnode, exp[i]-'0');		// 문자를 정수로 바꿔서 저장
        }
        else	// 연산자일 경우
        {
        	MakeRightSubTree(pnode, SPop(&stack));	// 스택에서 꺼내어 오른쪽 자식 노드로 연결
            MakeLeftSubTree(pnode, SPop(&stack));	// 스택에서 꺼내어 왼쪽 자식 노드로 연결
            SetData(pnode, exp[i]);
        }
        
        SPush(&stack, pnode);
    }
    
    return SPop(&stack);
}

이렇게 수식 트리로 작성하는 함수가 제대로 동작하는지 확인해야한다.

2) 소스파일 정의 - 수식 트리의 순회 (ExpressionTree.c)

수식 트리가 잘 구현되었는지 확인하기 위해서 아까 우리는 세 가지 방식인 전위, 중위, 후위 순회를 하면서 노드에 저장된 데이터를 출력하는 함수를 사용하려고 했다.
이 세 함수에 대한 정의를 구현해보자.

전위 순회하여 데이터를 출력한 결과 : 전위 표기법의 수식
중위 순회하여 데이터를 출력한 결과 : 중위 표기법의 수식
후위 순회하여 데이터를 출력한 결과 : 후위 표기법의 수식

이 함수들을 헤더파일에는 다음과 같이 선언했었다.

void ShowPrefixTypeExp(BTreeNode * bt);     // 전위 표기법 기반 출력
void ShowInfixTypeExp(BTreeNode * bt);      // 중위 표기법 기반 출력
void ShowPostfixTypeExp(BTreeNode * bt);    // 후위 표기법 기반 출력

이것을 그대로 활용하는 것이 아닌 이진 트리 구현에서 전위, 중위, 후위 순회한 것을 이용해서 함수를 정의해야한다.

// BinaryTree2.h에서 선언한 순회 함수
typedef void (*VisitFuncPtr)(BTData data);
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action);

때문에 노드에 저장된 데이터를 출력하는 함수는 다음과 같이 정의할 수 있다.

void ShowNodeData(int data)
{
	if(0<=data && data <=9)
    	printf("%d ", data);	// 피연산자 출력
    else
    	printf("%c ", data);	// 연산자 출력
}

그리고 이를 기반으로 헤더 파일에 선언된 함수들은 다음과 같이 채우면 된다.

void ShowPrefixTypeExp(BTreeNode * bt)	// 전위 표기법으로 수식 출력
{
	PreorderTraverse(bt, ShowNodeData);
}

void ShowInfixTypeExp(BTreeNode * bt)	// 중위 표기법으로 수식 출력
{
	InorderTraverse(bt, ShowNodeData);
}

void ShowPostfixTypeExp(BTreeNode * bt)	// 후위 표기법으로 수식 출력
{
	PostorderTraverse(bt, ShowNodeData);
}

위에서 정의한 함수들을 정리하면 아래와 같다.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include "ListBaseStack.h"
#include "BinaryTree2.h"

BTreeNode * MakeExpTree(char exp[])
{
    Stack stack;
    BTreeNode * pnode;

    int expLen = strlen(exp);
    int i;

    StackInit(&stack);

    for(i=0; i<expLen; i++)
    {
        pnode = MakeBTreeNode();
        
        if(isdigit(exp[i]))		// 피연산자일 경우
        {
        	SetData(pnode, exp[i]-'0');		// 문자를 정수로 바꿔서 저장
        }
        else	// 연산자일 경우
        {
        	MakeRightSubTree(pnode, SPop(&stack));	// 스택에서 꺼내어 오른쪽 자식 노드로 연결
            MakeLeftSubTree(pnode, SPop(&stack));	// 스택에서 꺼내어 왼쪽 자식 노드로 연결
            SetData(pnode, exp[i]);
        }
        
        SPush(&stack, pnode);
    }
    
    return SPop(&stack);
}

int EvaluateExpTree(BTreeNode * bt)
{
    // 잠시 후 구현할 함수
}

void ShowNodeData(int data)
{
	if(0<=data && data <=9)
    	printf("%d ", data);	// 피연산자 출력
    else
    	printf("%c ", data);	// 연산자 출력
}

void ShowPrefixTypeExp(BTreeNode * bt)	// 전위 표기법으로 수식 출력
{
	PreorderTraverse(bt, ShowNodeData);
}

void ShowInfixTypeExp(BTreeNode * bt)	// 중위 표기법으로 수식 출력
{
	InorderTraverse(bt, ShowNodeData);
}

void ShowPostfixTypeExp(BTreeNode * bt)	// 후위 표기법으로 수식 출력
{
	PostorderTraverse(bt, ShowNodeData);
}

3) 실행파일 정의 (ExpressionTreeMain.c)

지금까지 구현한 내용을 바탕으로 수식 트리의 헤더파일과 소스파일을 제시하고 이를 테스트하기 위한 main 함수(실행파일)을 정의하겠다.
그리고 실행을 위해 필요한 파일들을 정리하면 다음과 같다.

이진 트리 관련
: BinaryTree2.h, BinaryTree2.c
스택 관련
: ListBaseStack.h, ListBaseStack.c
수식 트리 관련
: ExpressionTree.h, ExpressionTree.c
main 함수 관련
: ExpressionMain.c

#include <stdio.h>
#include "ExpressionTree.h"

int main()
{
    char exp[] = "12+7*";
    BTreeNode * eTree = MakeExpTree(exp);

    printf("Prefix Type Expression: ");
    ShowPrefixTypeExp(eTree);
    printf("\n");

    printf("Infix Type Expression: ");
    ShowInfixTypeExp(eTree);
    printf("\n");

    printf("Postfix Type Expression: ");
    ShowPostfixTypeExp(eTree);
    printf("\n");

    printf("Result of Calculation: %d \n", EvaluateExpTree(eTree));

    return 0;
}

> gcc .\BinaryTree2.c .\ExpressionTree.c .\ExpressionTreeMain.c .\ListBaseStack.c
> .\a.exe
> 출력
Prefix Type Expression: * + 1 2 7
Infix Type Expression: 1 + 2 * 7
Postfix Type Expression: 1 2 + 7 *
Result of Calculation: 12720832

이제 여기서 아직 구현하지 않은 함수 EvaluateExpTree 정의하기와 중위 표기법에서 소괄호 출력 하기에 대해 추가로 더 알아보자.

4) 수식 트리 계산 함수 정의하기

수식 트리에 담겨있는 수식을 계산하는 함수를 정의해보자.
보통 트리이기 때문에 순회와 동일하게 단말 노드가 붙어 있는 서브 트리에서부터 계산해야 한다고 생각한다.
하지만 트리는 재귀적인 구조를 띄기 때문에 접근방법을 달리해야 한다.
먼저 함수의 정의는 다음과 같다.

int EvaluateExpTree(BTreeNode * bt)
{
	int op1, op2;
    
    op1 = GetData(GetLeftSubTree(bt));	// 첫 번째 피연산자
    op2 = GetData(GetRightSubTree(bt));	// 두 번째 피연산자
    
    switch(GetData(bt))		// 연산자 확인하여 연산 진행
    {
    case '+':
    	return op1+op2;
    case '-':
    	return op1-op2;
    case '*':    
    	return op1*op2;
    case '/':
    	return op1/op2;
    }
    return 0;
}

위 함수는 두 개의 자식 노드에 담겨있는 두 피연산자를 확인하고, 부모 노드에 저장된 연산자를 확인하여 연산을 진행한다.

근데 문제는 자식 노드에 피연산자가 아닌 서브 트리가 달려있는 경우 발생한다.
위 함수를 어떻게 develop 시켜야할까?
따라서 다음과 같이 수정한다면 서브 트리의 수식도 계산할 수 있을 것이다.

int EvaluateExpTree(BTreeNode * bt)
{
	int op1, op2;
    
    op1 = EvaluateExpTree(GetLeftSubTree(bt));		// 왼쪽 서브 트리 계산
    op2 = EvaluateExpTree(GetRightSubTree(bt));		// 오른쪽 서브 트리 계산
    
    switch(GetData(bt))		// 연산자 확인하여 연산 진행
    {
    case '+':
    	return op1+op2;
    case '-':
    	return op1-op2;
    case '*':    
    	return op1*op2;
    case '/':
    	return op1/op2;
    }
    return 0;
}

하지만 이렇게 함수를 정의한다면 자식 노드가 단말 노드일 경우 문제가 발생하고,
재귀함수의 탈출조건도 존재하지 않는다.

피연산자를 받는 문장(왼쪽, 오른쪽 서브 트리 계산 문장)을 보면 서브 트리를 대상으로 서브 트리의 주소 값을 전달하면 EvaluateExpTree 함수를 호출하고 있다.
따라서 함수의 탈출 조건은 "던잘된 것이 서브 트리가 추가로 달려있지 않은 단말 노드의 주소 값이라면 단말 노드에 저장된 피연산자를 반환"으로 하면 된다.

따라서 완성된 EvaluateExpTree 함수는 다음과 같다.

int EvaluateExpTree(BTreeNode * bt)
{
	int op1, op2;

	if(GetLeftSubTree(bt)==NULL && GetRightSubTree(bt)==NULL)	// 단말 노드의 경우
		return GetData(bt);

	op1 = EvaluateExpTree(GetLeftSubTree(bt));
	op2 = EvaluateExpTree(GetRightSubTree(bt));

	switch(GetData(bt))
	{
	case '+':
		return op1+op2;
	case '-':
		return op1-op2;
	case '*':
		return op1*op2;
	case '/':
		return op1/op2;
	}

	return 0;
}

위 함수 정의를 ExpressionTree.c 파일에 추가하고 다시 main 함수를 실행하면 다음과 같은 출력 결과를 얻을 수 있다.

Prefix Type Expression: * + 1 2 7 
Infix Type Expression: 1 + 2 * 7
Postfix Type Expression: 1 2 + 7 *
Result of Calculation: 21

+) 중위 표기법의 소괄호 출력

소괄호를 출력할 때 소괄호를 어디까지 출력해야할지 정해야한다.
그 이유는

3 + 2 * 7
3 + ( 2 * 7 )
( 3 + ( 2 * 7 ) )

위 세 수식이 모두 같은 수식이기 때문이다.
따라서 혼동이 없도록 연산자의 수와 소괄호 한쌍의 수를 일치시켜 (마지막 수식 방식) 중위 표기법을 출력할 것이다.
ShowInfixTypeExp 함수를 다음과 같이 수정하면 된다.

void ShowInfixTypeExp(BTreeNode * bt)
{
	if(bt == NULL)
    	return;
        
    if(bt->left != NULL || bt->right != NULL)
    	printf(" ( ");
    
    ShowInfixTypeExp(bt->left);		// 첫 번째 피연산자 출력
    ShowNodeData(bt->data);			// 연산자 출력
    ShowInfixTypeExp(bt->right);	// 두 번째 피연산자 출력
    
    if(bt->left != NULL || bt->right != NULL)
    	printf(" ) ");
}

수정 전 함수는 InorderTraverse 함수를 호출하는 형태였지만, 순회의 과정에서 소괄호를 출력해야 하기 때문에 직접 순회하는 코드를 작성했다.

따라서 수정된 코드를 실행하면 다음과 같은 결과를 얻을 수 있다.

Prefix Type Expression: * + 1 2 7 
Infix Type Expression:  (  ( 1 + 2  ) * 7  )
Postfix Type Expression: 1 2 + 7 *
Result of Calculation: 21

`<Review>`

오늘도 즐겁게 자료구조 공부를 했다.
요즘 계속해서 새로운 도전을 하고 있는데
트리를 보다보니 내가 하는 새로운 도전들이 자식 노드 하나하나가 되어 나중엔 최종 루트 노드에 도달할 수 있지 않을까 라는 생각을 하면서 공부했다.

트리를 표현해서 각 노드를 순회하는 것으로 노드의 값에 접근하고 원하는 노드 값을 가져와 연산할 수 있다는 것이 트리의 간편한 부분인 것 같다.
트리의 순회도 3가지나 있어 더 매력적으로 다가왔다.

앞으로 우선순위 큐와 힙에 대해 배울텐데 더 어려울 것이 예상되지만 기대가 된다...!
오늘도 고생했다~!

김민정

백엔드 코린이😁

이전 포스트

Chapter 07. 큐(Queue)

다음 포스트