Chapter 13. 테이블(Table)과 해쉬(Hash)

13-1. 빠른 탐색을 보이는 해쉬 테이블

AVL 트리는 탐색 키의 비교 과정을 거치면서 찾는 대상에 가까워지는 방식이기 때문에 원하는 바를 '단번에' 찾아내는 방식이라고 말하기 어렵다.
이러한 상황에서 더 높은 성능을 낼 수 있는 자료구조가 바로 '테이블 (Table)'이다.
AVL 트리의 탐색 연산이 $O(log_2n)$의 시간 복잡도를 보이는 반면에,
테이블 자료구조의 탐색 연산은 $O(1)$의 시간 복잡도를 보이니,
적용할 수 있는 상황에서는 테이블의 탐색 성능이 훨씬 좋다고 할 수 있다.

테이블(Table) 자료구조

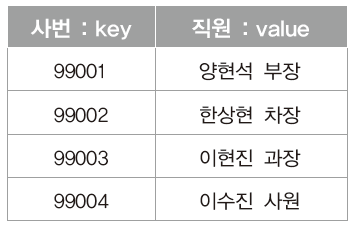
위 그림에서 보이는 것은 문서 편집에서 한번은 봤을 만한 '표'다.
그리고 이것이 바로 테이블이다.
하지만 자료구조의 관전에서 모든 표를 가리켜 테이블이라 하지 않는다.
표에 저장된 데이터의 형태가 "키(key)와 값(value)이 하나의 쌍을 이룰 때" 테이블로 구분 짓는다.
이렇듯 테이블에 저장되는 모든 데이터들은 이를 구분하는 '키'가 있어야 하고,
이 키는 데이터를 구분하는 기준이 되기 때문에 중복이 허용되지 않는다.
그리고 테이블에서는 키가 존재하지 않는 값은 저장할 수 없다.

이렇듯 테이블의 핵심은 키와 값이 하나의 쌍을 이뤄 저장되는 데이터 유형에 있다.
자료구조의 '테이블'은 '사전 구조'라고도 불리고 더불어 '맵(map)'이라고도 불린다.
사전구조라고 하는 이유는 테이블의 대표적인 예시가 사전이기 때문이다.
사전인 이유는 단어가 키가 되고 그 단어에 대한 설명 또는 내용이 값이 되기 때문이다.

1) 배열을 기반으로 하는 테이블

배열을 기반으로 누구나 쉽게 이해할 수 있는 간단한 예제를 살펴보자.
테이블 자료구조를 코드상으로 볼 수 있게 되어있다.

#include <stdio.h>

typedef struct _empInfo
{
    int empNum;     // 직원의 고유 번호
    int age;        // 직원의 나이
} EmpInfo;

int main()
{
    EmpInfo empInfoArr[100];
    EmpInfo ei;
    int eNum;

    printf("사번과 나이 입력: ");
    scanf("%d %d", &(ei.empNum), &(ei.age));
    empInfoArr[ei.empNum] = ei; // 바로 저장

    printf("확인하고 싶은 직원의 사번 입력: ");
    scanf("%d", %eNum);

    ei = empInfoArr[eNum];  // 바로 탐색
    printf("사번 %d, 나이 %d \n", ei.empNum, ei.age);
    return 0;
}

> 출력
사번과 나이 입력: 129 29
확인하고 싶은 직원의 사번 입력: 129
사번 129, 나이 29 

저장과 탐색의 원리만 확인할 수 있도록 main 함수를 간단하게 작성하였다.
선언된 구조체를 살펴보면 키와 값을 하나의 쌍으로 묶기 위해 정의되었다.
이 구조체를 기반으로 하는 배열 선언으로 EmpInfo empInfoArr[1000];로 했지만 이 배열을 가리켜 '테이블'이라 하기엔 많은 것이 부족해 보인다.
이것이 테이블이라 할 수 있으려면 키를 결정하였을 때 이를 기반으로 데이터를 단번에 찾아야되기 때문이다.
즉, 테이블에서 의미하는 키는 데이터를 (단번에) 찾는 도구가 되어야 한다.
그래서 저장으로 empInfoArr[ei.empNum] = ei;문장과
탐색으로 ei = empInfoArr[eNum];이 사용되었다.
이 두 개의 문장을 통해 알 수 있는 점은 직원의 고유번호를 인덱스 값으로 하여, 그 위치에 데이터를 저장한 것이다.
이렇듯 '키의 값은 저장위치'라는 관계를 형성해 단번에 데이터를 저장하고 단번에 데이터를 탐색할 수 있게 했다.
하지만 위 테이블은 더 많은 양의 데이터를 담기엔 배열이 작아보인다.
이러한 문제점은 테이블의 핵심인 해쉬와 관련된 내용이 빠져서 그렇다.

테이블에 의미를 부여하는 해쉬 함수와 충돌 문제

앞 예제에서 보인 테이블과 관련해서 지적된 문제점 두 가지는 다음과 같다.

• 직원 고유번호의 범위가 배열의 인덳 값으로 사용하기에 적당하지 않다.
• 직원 고유번호의 범위를 수용할 수 있는 매우 큰 배열이 필요하다.

이 두 가지 문제를 동시에 해결해주는 것이 바로 '해쉬 함수'이다.
해쉬 함수의 소개를 위해 앞 예제에서 "직원의 고유번호는 입사 년도 네 자리와 입사순서 네 자리로 구성된다."라는 가정을 추가해 다시 구현해보자.
예를 들어 2012년도에 세 번째로 입사한 직원의 고유번호는 "20120003"이 되고,
이어서 같은 해에 입사한 직원의 고유번호는 "20120004"가 된다.

#include <stdio.h>

typedef struct _empInfo
{
    int empNum;     // 직원의 고유 번호
    int age;        // 직원의 나이
} EmpInfo;

int GetHashValue(int empNum)
{
    return empNum % 100;
}

int main()
{
    EmpInfo empInfoArr[100];

    EmpInfo emp1={20120003, 24};
    EmpInfo emp2={20130012, 33};
    EmpInfo emp3={20170049, 27};

    EmpInfo r1, r2, r3;

    // 키를 인덱스 값으로 이용해서 저장
    empInfoArr[GetHashValues(emp1, empNum)] = emp1;
    empInfoArr[GetHashValues(emp2, empNum)] = emp2;
    empInfoArr[GetHashValues(emp3, empNum)] = emp3;

    // 키를 인덱스 값으로 이용해서 탐색
    r1 = empInfoArr[GetHashValues(20120003)];
    r2 = empInfoArr[GetHashValues(20130012)];
    r3 = empInfoArr[GetHashValues(20170049)];

    // 탐색 결과 확인
    printf("사번 %d, 나이 %d \n", r1.empNum, r1.age);
    printf("사번 %d, 나이 %d \n", r2.empNum, r2.age);
    printf("사번 %d, 나이 %d \n", r3.empNum, r3.age);

    return 0;
}

> 출력
사번 20120003, 나이 24 
사번 20130012, 나이 33 
사번 20170049, 나이 27

위 예제에서는 길이가 100인 배열을 선언했다.
직원의 수가 100명을 넘길 경우를 고려하지 않은 것이고,
데이터의 저장위치를 결정하는데 있어서 직원의 고유번호를 활용하되, GetHashValue라는 함수를 이용해 가공의 과정을 거쳤다.
위 함수에서 100으로 % 연산을 한 것은 여덟 자리의 수로 이뤄진 직원의 고유번호를 두 자리의 수로 변경한다는 의미를 가지고 있다.
실제로는 앞의 숫자 6개를 잘라낸 것이지만 이것도 변경의 일종이다.
그럼 100으로 나눠서 그 나머지를 취하는 연산을 함수 $f(x)$라 하자.
그럼 이 함수의 기능은 아래의 그림과 같이 표현할 수 있다.

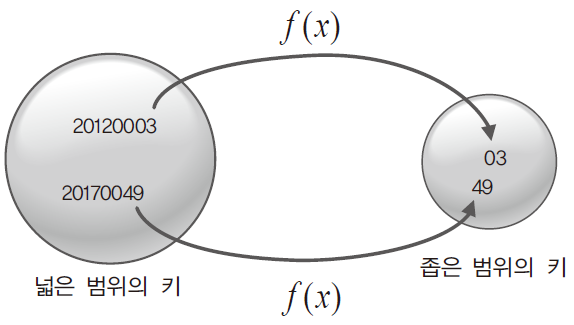
이 함수 $f(x)$를 가리켜 '해쉬 함수(hash function)'이라 한다.
그리고 이러한 해쉬 함수는 넓은 번위의 키를 좁은 범위의 키로 변경하는 역할을 한다.
실제로 위의 예제에서는 해쉬 함수와 관련해서 흔히 거론되는 % 연산자를 이용해서 여덟 자리의 키를 두 자리의 키로 바꿨다.

여기서 직원의 수가 100명을 넘어 직원 번호가 20210103이 형성되면 다음과 같은 문제가 발생한다.

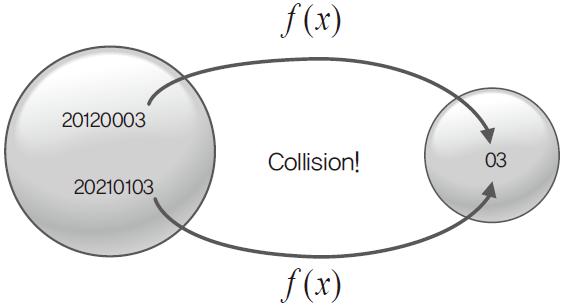
서로 다른 두 개의 키가 해쉬 함수를 통과했는데 그 결과가 03으로 모두 동일해 '충돌(collision)'이 발생한 것이다.
이러한 충돌은 배열의 길이를 늘리는 등의 방법으로 피해야 할 상황이 아니다.
이러한 충돌은 '해결해야 하는 상황'이고 충돌의 해결방법에 따라서 테이블의 구조가 달라지는 경우가 있을 정도로 충돌의 해결 방법은 테이블에 있어서 큰 의미를 갖는다.

2) 어느정도 갖춰진 테이블과 해쉬의 구현 예시

앞 예제들을 통해 테이블과 해쉬 함수의 구현에 대해 간단히 살펴보았다.
두 예제 모두 테이블의 구현 사례로는 약간의 부족한 점들이 있었다.
따라서 이번에는 어느 정도 갖춰진 테이블과 해쉬를 구현해 보려고 한다.
우선 테이블에 저장할 대상에 대한 헤더파일과 소스파일을 정의해보자.

• Person.h

  #ifndef __PERSON_H__
  #define __PERSON_H__
  
  #define STR_LEN 50
  
  typedef struct _person
  {
      int ssn;                // 주민등록번호
      char name[STR_LEN];     // 이름
      char addr[STR_LEN];     // 주소
  } Person;
  
  int GetSSN(Person *p);
  void ShowPerInfo(Person *p);
  Person * MakePersonData(int ssn, char * name, char * addr);
  
  #endif

• Person.c

  #include <stdio.h>
  #include <stdlib.h>
  #include <string.h>
  #include "PErson.h"
  
  int GetSSN(Person *p)
  {
      return p->ssn;
  }
  
  void ShowPerInfo(Person * p)
  {
      printf("SSN: %d \n", p->ssn);
      printf("Name: %s \n", p->name);
      printf("Address: %s \n", p->addr);
  }
  
  Person * MakePersonData(int ssn, char * naem, char * addr)
  {
      Person * newP = (Person *)malloc(sizeof(Person));
      newP->ssn = ssn;
      strcpy(newP->name, name);
      strcpy(newP->addr, addr);
      return newP;
  }

위의 헤더파일에 정의된 Person 구조체의 변수가 (정확히는 구조체 변수의 주소 값이) 테이블에 저장될 값이다.
그리고 그 중에서 구조체의 멤버 ssn(주민등록번호)를 키로 결정하였다.
키를 별도로 추출하는데 사용하기 위해서 GetSSN 함수를 정의했다.
그리고 Person 구조체 변수의 생성 및 초기화의 편의를 위해서 MakePersonData 함수도 정의했다.
이어서 테이블의 구현과 관련이 있는 파일들을 살펴보자.
첫 번째로 볼 헤더파일은 테이블의 슬롯을 정의한 헤더파일이다.
슬롯(Slot)이 무엇인지는 코드를 먼저 살펴보고 설명을 할 예정이다.

• Slot.h

  #ifndef __SLOT_H__
  #define __SLOT_H__
  
  #include "Person.h"
  
  typedef int Key;    // 주민등록번호
  typedef Person * Value;
  
  enum SlotStatus {EMPTY, DELETED, INUSE};
  
  typedef struct _slot
  {
      Key key;
      Value val;
      enum SlotStatus status;
  } Slot;
  
  #endif

  슬롯(slot)이란 테이블을 이루는, 테이블을 저장할 수 있는 각각의 공간을 의미한다.
  그리고 위의 typedef 선언에서도 보이듯 키와 값은 다음과 같이 결정했다.

  • 키 : 주민등록번호
  • 값 : Person 구조체 변수의 주소 값

  그리고 enum 선언을 통해 슬롯의 상태를 나타내는 상수 EMPTY, DELETED, INUSE 가 정의되었고, 이를 기반으로 다음과 같이 Slot 구조체의 멤버를 선언했다.
  enum SlotStatus status;

  슬롯의 상태를 나타내는 상수 각각이 의미하는 바는 다음과 같다.

  • EMPTY: 이 슬롯에는 데이터가 저장된 바 없다.
  • DELETED: 이 슬롯에는 데이터가 저장된 바 있으나 현재는 비워진 상태다.
  • INUSE: 이 슬롯에는 현재 유효한 데이터가 저장되어 있다.

  이 중에서 EMPTY와 INUSE의 필요성은 이해가 되지만, 사실 DELETED의 필요성에 대해서는 의문이 든다.
  DELETED의 필요성은 충돌의 해결책에 대해 배우면서 함께 배울 예정이다.

이제 테이블의 실질적인 구현에 해당하는 헤더파일과 소스파일에 대해 알아보자.

• Table.h

  #ifndef __TABLE_H__
  #define __TABLE_H__
  
  #include "Slot.h"
  
  #define MAX_TBL 100
  
  typedef int HashFunc(Key k);
  
  typedef struct _table
  {
      Slot tbl[MAX_TBL];
      HashFunc * hf;
  } Table;
  
  // 테이블의 초기화
  void TBLInit(Table * pt, HashFunc * f);
  
  // 테이블에 키와 값을 저장
  void TBLInsert(Table * pt, Key k, Value v);
  
  // 키를 근거로 테이블에서 데이터 삭제
  Value TBLDelete(Table * pt, Key k);
  
  // 키를 근거로 테이블에서 데이터 탐색
  Value TBLSearch(Table * pt, Key k);
  
  #endif

• Table.c

  #include <stdio.h>
  #include <stdlib.h>
  #include "Table.h"
  
  void TBLInit(Table * pt, HashFunc * f)
  {
      int i;
  
      // 모든 슬롯 초기화
      for(i=0; i<MAX_TBL; i++)
          (pt->tbl[i]).status = EMPTY;
  
      pt->hf = f; // 해쉬 함수 등록    
  }
  
  void TBLInsert(Table * pt, Key k, Value v)
  {
      int hv = pt->hf(k);
      pt->tbl[hv].val = v;
      pt->tbl[hv].key = k;
      pt->tbl[hv].status = INUSE;
  }
  
  Value TBLDelete(Table * pt, Key k)
  {
      int hv = pt->hf(k);
  
      if((pt->tbl[hv]).status != INUSE)
          return NULL;
      else
      {
          (pt->tbl[hv]).status = DELETED;
          return (pt->tbl[hv]).val;   // 소멸 대상의 값 반환
      }
  }
  
  Value TBLSearch(Table * pt, Key k)
  {
      int hv = pt->hf(k);
  
      if((pt->tbl[hv]).status != INUSE)
          return NULL;
      else
          return (pt->tbl[hv]).val;   // 탐색 대상의 값 반환
  }

직접 정의한 해쉬 함수를 등록하도록 디자인되었다는 사실과 Slot 배열로 테이블을 구성했다는 사실에 주목하면 코드를 쉽게 이해할 수 있다.
위 테이블을 대상으로 하는 main 함수(실행파일)은 다음과 같다.

• SimpleHashMain.c

  #include <stdio.h>
  #include <stdlib.h>
  #include "Person.h"
  #include "Table.h"
  
  int MyHashFunc(int k)
  {
      return k % 100;
  }
  
  int main()
  {
      Table myTbl;
      Person * np;
      Person * sp;
      Person * rp;
  
      TBLInit(&myTbl, MyHashFunc);
  
      // 데이터 입력
      np = MakePersonData(20120003, "Lee", "Seoul");
      TBLInsert(&myTbl, GetSSN(np), np);
  
      np = MakePersonData(20130012, "Kim", "Jeju");
      TBLInsert(&myTbl, GetSSN(np), np);
  
      np = MakePersonData(20170049, "Han", "Kangwon");
      TBLInsert(&myTbl, GetSSN(np), np);
  
      // 데이터 탐색
      sp = TBLSearch(&myTbl, 20120003);
      if(sp!= NULL)
          ShowPerInfo(sp);
  
      sp = TBLSearch(&myTbl, 20130012);
      if(sp!= NULL)
          ShowPerInfo(sp);
  
      sp = TBLSearch(&myTbl, 20170049);
      if(sp!= NULL)
          ShowPerInfo(sp);
  
      // 데이터 삭제
      rp = TBLDelete(&myTbl, 20120003);
      if(rp!= NULL)
          free(rp);
  
      rp = TBLDelete(&myTbl, 20130012);
      if(rp!= NULL)
          free(rp);
  
      rp = TBLDelete(&myTbl, 20170049);
      if(rp!= NULL)
          free(rp);
  
      return 0;
  }
  
  > gcc .\Person.c .\SimpleHashMain.c .\Table.c
  > .\a.exe
  > 출력
  SSN: 20120003 
  Name: Lee 
  Address: Seoul
  
  SSN: 20130012
  Name: Kim
  Address: Jeju
  
  SSN: 20170049
  Name: Han
  Address: Kangwon

좋은 해쉬 함수의 조건

좋은 해쉬 함수의 조건을 언급하기에 앞서 좋은 해쉬 함수를 사용한 결과와 좋지 않은 해쉬 함수를 사용한 결과를 비교해보자.
먼저 좋은 해쉬 함수를 사용한 결과는 다음과 같다.

위 그림은 테이블의 메모리 상황을 표현한 것인데 검은 영역은 데이터가 채워진 슬롯을 의미한고, 흰 영역은 빈 슬롯을 의미한다.
데이터가 테이블의 전체 영역에 고루 분포되어 있는 것을 알 수 있는데,
이렇듯 고루 분포된다는 것은 그만큼 충돌이 발생할 확률이 낮다는 것을 의미한다.
충돌의 해결책이 마련되어 있다 하더라도 충돌이 덜 발생해야 데이터의 저장, 삭제 및 탐색의 효율을 높일 수 있다.
때문에 좋은 해쉬 함수는 '충돌을 덜 일으키는 해쉬 함수'라고도 할 수 있다.

반면에 좋지 못한 해쉬 함수는 다음과 같은 사용결과를 보여준다.

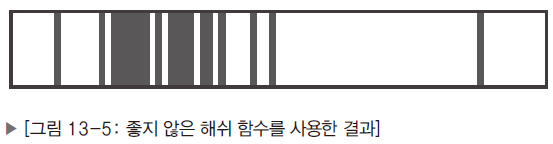
테이블의 특정 영역에 데이터가 몰려 있고 이는 해쉬 함수가 특정 영역에 데이터가 몰리도록 '해쉬 값'을 생성한 결과다. (해쉬 값이란 해쉬 함수가 만들어 낸 값이다.)
때문에 충돌이 발생할 확률이 그만큼 높은 상황이다.
좋은 해쉬 함수를 디자인하는 방법은 키의 특성에 따라 달라지기 때문에 "키의 일부분을 참조하여 해쉬 값을 만들지 않고, 키의 전체를 참조하여 해쉬 값을 만들어야" 일반적으로 좋은 해쉬 함수를 정의할 수 있다고 한다.
아무래도 적은 수의 데이터를 조합하여 해쉬 값을 생성하는 것보다 많은 수의 데이터를 조합하여 해쉬 값을 생성했을 때 보다 다양한 값의 생성을 기대할 수 있기 때문이다.

자릿수 선택(Digit Selection) 방법과 자릿수 폴딩(Digit Folding) 방법

좋은 해쉬 함수의 디자인 방법은 위에서도 언급했지만 키의 특성에 따라 달라진다.
때문에 해쉬 함수의 디자인에 있어서 절대적인 방법은 존재하지 않는다.
다만 위의 조언, 키 전체를 참조하는 방법과 관련해서는 다양한 방법이 소개되고 있는데,

그 중 하나는 "자릿수 선택 방법으로" 여덟 자리의 수로 이뤄진 키에서 다양한 해쉬 값 생성에 도움을 주는 네 자리의 수를 뽑아서 해쉬 값을 생성한다는 것이다.
키의 특정 위치에서 중복의 비율이 높고나, 아예 공통으로 들어가는 값이 있다면, 이를 제외한 나머지를 가지고 해쉬 값을 생성하는 방법이다.

그리고 이와 유사한 방법으로 "비트 추출 방법"이 있다.
탐색 키의 비트 열에서 일부를 추출 및 조합하는 방법이다.

그 다음 방법으로는 "자릿수 폴딩"이다.
종이를 접듯이 숫자를 겹치게 하여 더한 결과를 해쉬 값으로 결정하는 방법이다.
예를 들어 아래 그림과 같이 숫자가 적힌 종이를 삼등분으로 접으면

27, 34, 19로 나뉘고 이 두 자릿수 세 개를 모두 더하면 80이 된다.
이를 해쉬 값이라 하면 여섯 자리의 숫자를 모두 반영하여 얻은 결과가 된다.

이 외에도 키를 제곱하여 그 중 일부를 추출하는 방법, 폴딩의 과정에서 덧셈 대신 XOR 연산을 하는 방법, 그리고 둘 이상의 방법을 조합하는 방법 등 통계적으로 넓은 분포를 보이는 다양한 방법들이 있다.

---

13-2. 충돌(Collision) 문제의 해결책

테이블의 핵심 주제라 할 수 있는 충돌(Collision)에 대해서 고민해볼 차례다.
충돌의 해결책은 대단한 것은 아니고, 충돌이 발생한 자리를 대신해서 빈 자리를 찾아주는 것이다.
이 빈 자리를 찾는 방법에 따라서 해결책이 구분된다.

선형 조사법(Linear Probing)과 이차 조사법(Quadratic Probing)

충돌이 발생했을 때 그 옆자리가 비었는지 살펴보고, 비었을 경우 그 자리에 대신 저장하는 것이 바로 선형 조사법(Linear Probing) 이다.
예를 들어 해쉬 함수 $f(x) = key$ % $7$가 있고 테이블의 내부 저장소가 배열이라고 생각해보자.
키가 9인 데이터가 저장될 때 해쉬 값이 2가 되므로 다음 그림과 같이 인덱스가 2인 위치에 저장이 된다.

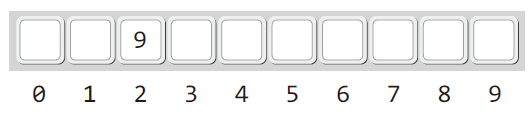
이어서 키가 2인 데이터가 등장했다고 생각해보자. 이 경우 해쉬 값이 2이기 때문에 앞서 저장한 키가 9인 데이터와 충돌이 발생한다.
이렇게 충돌이 발생했을 때 인덱스 값이 3인 바로 옆자리를 살피는 것이 선형 조사법이다.
따라서 키가 2인 두 번째 데이터의 저장결과는 다음 그림과 같이 된다.

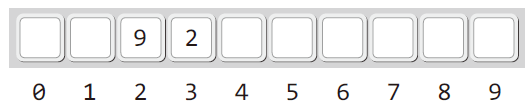
물론 옆자리가 비어있지 않을 경우 한 칸 더 이동해서 자리를 살피게 된다.
정리하면 $k$의 키에서 충돌 발생시 선현 조사법의 조사 순서(빈자리를 찾는 순서)는 다음과 같이 전개된다.

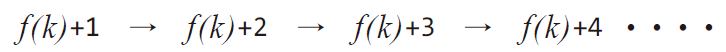
그런데 이러한 선형 조사법은 충돌 횟수가 증가함에 따라서 '클러스터(cluster)현상'
즉, 특정 영역에 데이터가 집중적으로 몰리는 현상이 발생한다는 단점이 있다.
그리고 이러한 클러스터 현상은 충돌의 확률을 높이는 직접적인 원인이 된다.
그렇다면 선형 조사법의 이러한 단점을 극복하려면 어떤 방법을 사용하면 좋을까?

바로 옆 빈자리를 찾는 것이 아닌 좀 먼 곳에서 빈자리를 찾으면 된다!
이러한 생각을 근거로 탄생한 것이 이차 조사법(Quadratic Probing) 이다.
충돌 발생시 이차 조사법의 조사 순서는 다음과 같이 전개된다.

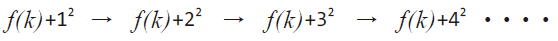
선형 조사법은 충돌 발생시 $n$칸 옆의 슬롯을 검사한다면,
이차 조사법은 충돌 발생시 $n^2$칸 옆의 슬롯을 검사한다.
이렇듯 좀 멀리서 빈 공간을 찾으려는 노력이 이차 조사법에 담겨있다.
물론 이차 조사법에도 나름의 문제가 있는데 이는 잠시 후 '이중 해쉬'를 통해 배울 것이다.

이번에는 슬롯의 상태 정보를 별도로 관리(EMPTY, DELETED, INUSE)해야 하는 이유에 대해서 알아보자.
앞에서 본 배열 형태를 가진 해쉬 함수에서 두 번째로 해쉬 값이 2인 데이터를 저장할 경우 3에 저장된 경우를 생각해보자. (아래 그림)

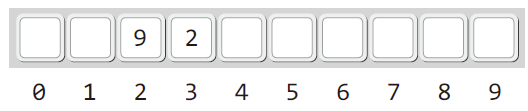
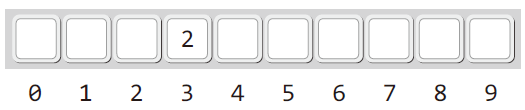
위 그림은 값이 9라 키 값이 2인 데이터가 삭제된 이후 상황이다.
여기서 인덱스 값이 2인 부분은 DELETED가 되고 3인 부분이 INUSE, 나머지 부분들은 EMPTY가 된다.
여기서 각 상태가 의미하는 바는 앞에서 한번 배웠지만 아래와 같이 정리할 수 있다.

• EMPTY: 이 슬롯에는 데이터가 저장된 바 없다.
• DELETED: 이 슬롯에는 데이터가 저장된 바 있으나 현재는 비워진 상태다.
• INUSE: 이 슬롯에는 현재 유효한 데이터가 저장되어 있다.

여기서 중점을 두어야할 부분은 DELETED 상태 정보가 있어 EMPTY 상태와 구분되어 있다는 점이다.
이 이유는 키가 2인 데이터의 탐색 과정을 살펴보면 알 수 있다.
키가 2인 데이터의 탐색을 진행하기 위해서는 %7의 해쉬 함수를 거친다.
그리고 그 결과로 얻은 2를 인덱스 값으로 하여 탐색을 진행하게 된다.
만약에 그 위치의 슬롯 상태가 EMPTY라면 데이터가 존재하지 않는다고 판단하여 탐색을 종료하게 된다.
반면 DELETED 상태일 경우 충돌이 발생했을 경우를 의심해서 선형 조사법에 근거한 탐색의 과정을 진행해야 한다.
따라서 선형, 이차 조사법과 같은 충돌의 해결책을 적용하기 위해서는 슬롯의 상태가 DELETED인 경우를 포함시켜야 하는 것이다.
선형, 이차 조사법을 적용하였다면 탐색의 과정에서도 이를 근거로 충돌을 의심하는 탐색의 과정을 포함시켜야 한다.
이렇듯 슬롯의 DELETED 상태는 충돌의 해결책과 관련이 있다.

이중 해쉬(Double Hash)

앞서 충돌을 해결하기 위해 제시된 방법은 선형 조사법과 이차 조사법이었다.
이차 조사법의 문제점으로는 해쉬 값이 같으면 충돌 발생시 빈 슬롯을 찾기 위해서 접근하는 위치가 늘 동일하다 점이 있다.
예를 들어서 해쉬 값을 기준으로 $f(k)$에서 충돌이 발생한다면 (해쉬 값 $f(k)$가 동일하다면) $k$가 다르더라도 다음의 순서대로 일정하게 빈 슬롯을 찾게 된다.

• 첫 번째 관찰 위치 : $f(k)+1^2$ (1칸 옆의 슬롯)
• 두 번째 관찰 위치 : $f(k)+2^2$ (4칸 옆의 슬롯)
• 세 번째 관찰 위치 : $f(k)+3^2$ (9칸 옆의 슬롯)
• 네 번째 관찰 위치 : $f(k)+4^2$ (16칸 옆의 슬롯)

이렇듯 해쉬 값이 같을 경우 빈 슬롯을 찾아서 접근하는 위치가 동일하기 때문에 선형 조사법보다는 낮지만, 접근이 진행되는 슬롯을 중심으로 클러스터 현상이 발생할 확률은 여전히 높을 수 밖에 없다.
이 단점은 이중 조사법에서 멀리서 빈 공간을 찾는 대신 규칙적인 방식으로 빈 공간을 선택하는 것이 아닌 불규칙하게 구성하면 해결할 수 있다.
이러한 것을 반영한 것이 '이중 해쉬'방법이다.

이중 해쉬 방법에서는 두 개의 해쉬 함수를 마련한다.
하나는 앞에서 본 것과 마찬가지로 키를 근거로 저장위치를 결정하는 것이고,
다른 하나는 충돌이 발생했을 때 몇 칸 뒤에 위치한 슬롯을 살펴볼지 그 거리를 결정하기 위한 것이다.

• 1차 해쉬 함수: 키를 근거로 저장위치를 결정하기 위한 것
• 2차 해쉬 함수: 충돌 발생시 몇 칸 뒤를 살필지 결정하기 위한 것

이해를 돕기 위해 이중 해쉬의 두 해쉬 함수를 예시로 들어보자.
먼저 배열을 저장소로 하는 테이블이 있다고 가정한다.
그리고 그 테이블의 해쉬 함수는 다음과 같이 정의되어 있다.

• 1차 해쉬 함수: $h1(k) = k$ % $15$
• 2차 해쉬 함수: $h2(k) = 1 + (k$ % $c )$

2차 해쉬 함수 식은 절대적인 것은 아니지만 일반적인 형태로 많이 사용한다.
2차 해쉬 함수의 상수 $c$는 1차 해쉬 함수를 % 15로 결정한 것을 보아 배열의 길이가 15라고 예상할 수 있고, 그럼 15보다 작으면서도 소수(prime number) 중 하나로 결정할 수 있다.

따라서 다음과 같이 해쉬 함수를 정리할 수 있다.

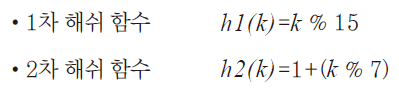
상수 $c$는 7말고 다른 소수로 정해도 상관 없다.

왜 2차 해쉬 함수식은 일반적으로 $h2(k) = 1 + (k$ % $c )$를 사용할까?
먼저 1을 더하는 이유는 2차 해쉬 값이 0이 되는 것을 막기 위해서다.

그 다음 상수 $c$를 15보다 작은 소수로 결정하는 이유는 뭘까?
그 이유는 가급적 2차 해쉬 값이 1차 해쉬 값을 넘어서지 않게 하기 위함이다.
예를 들어서 1차 해쉬의 최대 값이 14인데 2차 해쉬 값이 최대 32라면 빈 자리를 찾아서 몇번 반복해서 돌아야할지 모르기 때문이다.

그렇다면 소수로 결정하는 이유는 뭘까?
이는 소수를 선택했을 때 클러스터 현상이 발생할 확률을 현저히 낮춘다는 통계를 근거로 정한 것이다.

마지막으로 2차 해쉬 함수의 활용에 대한 예를 하나 들겠다.
앞서 정의한 1차 해쉬 함수에 3개의 키 3, 18, 33을 적용해서 해쉬 값을 구하면 다음과 같다.

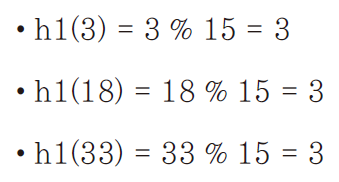
때문에 키가 3, 18, 33인 데이터를 순서대로 저장하면,
키가 18인 데이터를 저장할 때와 키가 33인 데이터를 저장할 때 충돌이 발생한다.
따라서 이 두 개의 키를 대상으로 2차 해쉬 값을 계산한다.

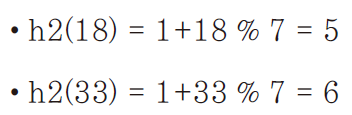
2차 해쉬 값은 달라지게 되고 이 2차 해쉬 값을 근거로 빈 슬롯을 찾는 과정은 각각 다음과 같이 전개된다.

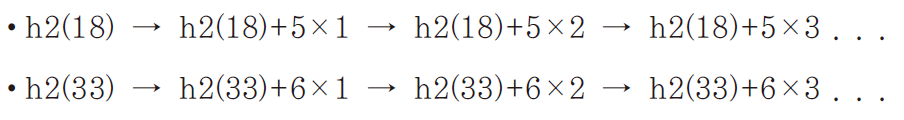
이렇듯 2차 해쉬 값의 크기만큼 건너 뛰면서 빈 슬롯을 찾게 되므로, 키가 다르면 건너 뛰는 길이도 달라진다.
따라서 클러스터 현상의 발생 확률을 낮출 수 있다.

체이닝(Chaining)

앞에서 본 유형의 충돌 해결 방법들을 가리켜 '열린 어드레싱 방법(open addressing method)'라 한다.
이는 충돌이 발생하면 다른 자리에 대신 저장한다는 의미가 담겨져 있다.
반면, 이번에 배울 유형의 방법을 가리켜 '닫힌 어드레싱 방법(closed addressing method)'라 한다.
이는 무슨 일이 있어도 자신의 자리에 저장한다는 의미이다.
충돌이 발생해도 자신의 자리에 들어가기 위해서는 여러 개의 자리를 마련하는 수 밖에 없다.
여러 개의 자리를 마련하는 방법으로는 배열을 이용하는 방법과 연결 리스트를 이용하는 방법이 있다.

배열을 이용해 자리를 여러 개 마련하는 방법은 다음과 같다.

위 그림과 같이 2차원 배열을 구성해서 해쉬 값 별로 다수의 슬롯을 마련할 수 있다.
하지만 이는 닫힌 어드레싱 방법 중에 흔히 언급되는 방법이 아니다.
충돌이 발생하지 않을 경우 메모리 낭비가 심하고, 충돌의 최대 횟수를 정해야 하는 부담이 있기 때문이다.
따라서 '체이닝(Chaining)'이라는 연결 리스트를 이용해 슬롯을 연결하는 방법이 닫힌 어드레싱 방법을 대표한다.

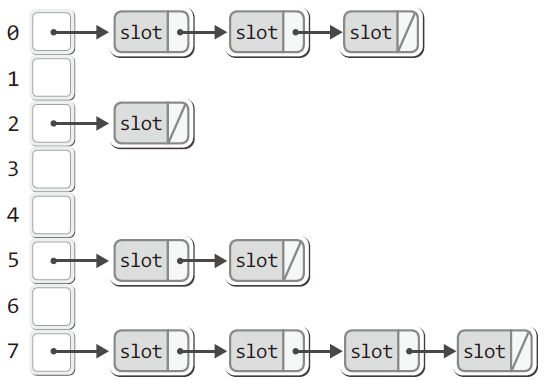
위 그림처럼 슬롯을 생성해서 연결 리스트의 모델로 연결하는 방식으로 충돌 문제를 해결하는 것이 체이닝 방법이다.
체이닝 방법을 적용하면 하나의 해쉬 값에 다수의 슬롯을 둘 수 있다.
따라서 탐색을 위해서는 동일한 해쉬 값으로 묶여있는 연결된 슬롯을 모두 조사해야 한다는 불편함이 있다.
하지만 해쉬 함수를 잘 정의한다면 (충돌의 확률이 높지 않다면) 연결된 슬롯의 길이는 부담스러운 정도가 아니게 될 수 있다.

충돌 문제 해결을 위한 체이닝의 구현

앞서 구현한 테이블을 변경, 확장하는 형태로 체이닝 방법을 구현해보자.

위 파일들을 사용하고 추가로 동일한 해쉬 값의 슬롯을 연결 리스트로 연결하기 위해서 Chapter 04에서 구현한 연결 리스트 (DLinkedList.h / DLinkedList.c)) 를 활용할 것이다.

구현한 테이블에서 Person.h파일과 Person.c 파일에는 변함이 없다.

• Slot2.h

  #ifndef __SLOT2_H__
  #define __SLOT2_H__
  
  #include "Person.h"
  
  typedef int Key;
  typedef Person * Value;
  
  typedef struct _slot
  {
      Key key;
      Value val;
  } Slot;
  
  #endif

  Slot.h 파일을 수정하였고 파일명을 변경해준다.
  슬롯의 상태 정보를 표시하기 위한 enum 선언과 관련 구조체의 멤버가 삭제되었다.
  열린 어드레싱 방법에서는 슬롯의 상태 정보를 표시해야 했지만, 닫힌 어드레싱 방법에서는 슬롯의 상태 정보를 표시할 필요가 없기 때문이다.
  따라서 그에 대한 선언들이 생략되었다.

• Table2.h

  #ifndef __TABLE2_H__
  #define __TABLE2_H__
  
  #include "Slot2.h"
  #include "DLinkedList.h"
  
  #define MAX_TBL 100
  
  typedef int HashFunc(Key k);
  
  typedef struct _table
  {
      List tbl[MAX_TBL];
      HashFunc * hf;
  } Table;
  
  // 테이블의 초기화
  void TBLInit(Table * pt, HashFunc * f);
  
  // 테이블에 키와 값을 저장
  void TBLInsert(Table * pt, Key k, Value v);
  
  // 키를 근거로 테이블에서 데이터 삭제
  Value TBLDelete(Table * pt, Key k);
  
  // 키를 근거로 테이블에서 데이터 탐색
  Value TBLSearch(Table * pt, Key k);
  
  #endif

  Table.h 파일을 수정하였고 파일명을 변경해준다.
  Table.h 파일과 가장 큰 차이점은 테이블의 저장소였던 Slot형 배열을 List형 배열로 바꿨다는 점이다.
  이를 위해서 헤더 파일 DLinkedList.h를 포함하는 선언문도 추가되었다.
  배열의 각 요소가 연결 리스트로 이뤄진 셈이 되었다.

여기까지는 기본적인 수준의 변경이다.
하지만 이제부터는 연결 리스트와 구조체 Slot의 관계에 대해 생각해봐야 한다.
두 가지의 경우에 대해 생각해 볼 수 있는데,
첫 번째, 구조체 Slot을 연결 리스트의 노드로 활용하는 방법이다.

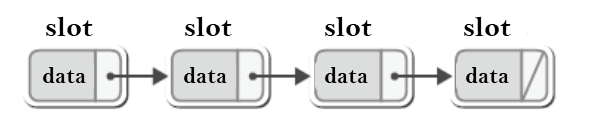
이 방법은 기존에 구현해 놓은 리스트 자료구조를 활용하지 않고 리스트 자료구조와 관련된 코드를 직접 새로 작성하는 경우에 생각해 볼 수 있는 방법이다.
이 방법을 택하려면 구조체 Slot을 다음과 같이 정의해야 한다.

typedef struct _slot		// 구조체 Slot이 연결 리스트의 노드 역할을 겸하는 구조
{
	Key key;
    Value val;
    struct _slot * next;	// 다음 노드를 가리키는 포인터 변수
} Slot;

다른 방법으로 슬롯과 노드를 엄연히 구분하는 보다 좋은 구조가 있다.
이는 노드에 슬롯의 주소 값을 저장하는 형태로 노드에 저장할 데이터의 형을 결정하는 typedef 선언문이 다음과 같이 추가될 필요가 있다.

typedef Slot * Data;		// 노드에 저장할 데이터는 Slot형 변수의 주소 값

typedef struct _node
{
	Data data;
    struct _node * next;
} Node;

위와 유사한 방법으로 다음 그림과 같이 슬롯이 노드의 멤버가 되게 하는 방법이 있다.
이 방법도 슬롯과 노드를 구분하는 방법과 비슷하다.

그림만 봐서는 슬롯과 노드가 구분되지 않는다고 볼 수 있다.
하지만 구분된 것으로 보는 것이 맞고, 코드에서 이를 확인할 수 있다.
위의 방법을 구현하기 위해서 노드가 저장할 데이터의 형을 결정하는 typedef 선언문을 다음과 같이 작성해야 한다.

typedef Slot Data;		// 노드에 저장할 데이터는 Slot형 변수다.

typedef struct _node
{
	Data data;
    struct _node * next;
} Node;

이렇게 해서 체이닝의 구현을 위해 다음 두 가지 방법이 있다는 것을 배웠다.

• 슬롯이 연결 리스트의 노드 역할을 하게 하는 방법
• 연결 리스트의 노드와 슬롯을 구분하는 방법

이 중에서 노드와 슬롯을 구분하는 방법을 선택하면 연결 리스트 간련 코드와 테이블 관련 코드의 구분이 용이하기 때문에 이 방법으로 배울 예정이다.
(이 방법을 선택해야 앞에서 구현한 연결 리스트를 활용할 수 있기도 하다.)
따라서 연결 리스트의 노드와 슬롯을 구분하는 방법으로 체이닝을 구현해보자.

• DLinkedList.h
  연결 리스트를 구현한 헤더파일로 다음과 같이 typedef 선언을 변경해야 한다.

  #ifndef __D_LINKED_LIST_H__
  #define __D_LINKED_LIST_H__
  
  #include "Slot2.h"  // 헤더파일 선언문 추가
  
  #define TRUE        1
  #define FALSE       0
  
  typedef Slot LData; // 변경된 typedef 선언문
  
  typedef struct _node
  {
      LData data;
      struct _node* next;
  } Node;
  
  typedef struct _linkedList
  {
      Node * head;						
      Node * cur;							
      Node * before;						
      int numOfData;						
      int (*comp)(LData d1, LData d2);
  } LinkedList;
  
  typedef LinkedList List;
  
  // .... 생략
  
  #endif

• Table2.c
  : 데이터 저장의 형태가 배열이 아닌 연결 리스트로 변경되었고 Table2.h에 선언된 함수를 재정의하기 위해서 Table.c 파일을 수정하고 파일명을 바꾼다.

  #include <stdio.h>
  #include <stdlib.h>
  #include "Table2.h"         // 수정
  #include "DLinkedList.h"    // 추가
  
  void TBLInit(Table * pt, HashFunc * f)
  {
      int i;
  
      for(i=0; i<MAX_TBL; i++)
          ListInit(&(pt->tbl[i]));    // 수정
  
      pt->hf = f;
  }
  
  void TBLInsert(Table * pt, Key k, Value v)
  {
      int hv = pt->hf(k);
      Slot ns = {k, v};
  
      if(TBLSearch(pt,k) != NULL) // 키가 중복이라면
      {
          printf("키 중복 오류 발생 \n");
          return;
      }
      else
      {
          LInsert(&(pt->tbl[hv]), ns);
      }
  }
  
  Value TBLDelete(Table * pt, Key k)
  {
      int hv = pt->hf(k);
      Slot cSlot;
  
      if(LFirst(&(pt->tbl[hv]), &cSlot))
      {
          if(cSlot.key == k)
          {
              LRemove(&(pt->tbl[hv]));
              return cSlot.val;
          }
          else
          {
              while(LNext(&(pt->tbl[hv]), &cSlot))
              {
                  if(cSlot.key == k)
                  {
                      LRemove(&(pt->tbl[hv]));
                      return cSlot.val;
                  }
              }
          }
      }
  
      return NULL;
  }
  
  Value TBLSearch(Table * pt, Key k)
  {
      int hv = pt->hf(k);
      Slot cSlot;
  
      if(LFirst(&(pt->tbl[hv]), &cSlot))
      {
          if(cSlot.key == k)
          {
              return cSlot.val;
          }
          else
          {
              while(LNext(&(pt->tbl[hv]), &cSlot))
              {
                  if(cSlot.key == k)
                  {
                      return cSlot.val;
                  }
              }
          }
      }
  
      return NULL;
  }

  연결 리스트의 탐색과정에서 처음에는 LFirst, 그 다음부터는 LNext 함수를 호출한다는 것과 LRemove 함수가 호출되었을 때 앞서 LFirst 또는 LNext 호출 시 반환되는 값이 삭제된다는 것만 알아도 위 코드들을 이해하기 어렵지 않을 것이다. (아뇨 전 어렵습니다...)

• ChainedTableMain.c
  : 마지막으로 실행 파일인 Main 함수를 소개로 정리해보겠다.

  #include <stdio.h>
  #include <stdlib.h>
  #include "Person.h"
  #include "Table2.h"
  
  int MyHashFunc(int k)
  {
      return k % 100;
  }
  
  int main(void)
  {
      Table myTbl;
      Person * np;
      Person * sp;
      Person * rp;
  
      TBLInit(&myTbl, MyHashFunc);
  
      // 데이터 입력
      np = MakePersonData(900254, "Lee", "Seoul");
      TBLInsert(&myTbl, GetSSN(np), np);
  
      np = MakePersonData(900139, "KIM", "Jeju");
      TBLInsert(&myTbl, GetSSN(np), np);
  
      np = MakePersonData(900827, "HAN", "Kangwon");
      TBLInsert(&myTbl, GetSSN(np), np);
  
      // 데이터 탐색
      sp = TBLSearch(&myTbl, 900254);
      if(sp != NULL)
          ShowPerInfo(sp);
  
      sp = TBLSearch(&myTbl, 900139);
      if(sp != NULL)
          ShowPerInfo(sp);
  
      sp = TBLSearch(&myTbl, 900827);
      if(sp != NULL)
          ShowPerInfo(sp);
  
      // 데이터 삭제
      rp = TBLDelete(&myTbl, 900254);
      if(rp != NULL)
          free(rp);
  
      rp = TBLDelete(&myTbl, 900139);
      if(rp != NULL)
          free(rp);
  
      rp = TBLDelete(&myTbl, 900827);
      if(rp != NULL)
          free(rp);
  
      return 0;
  }
  
  > gcc .\ChainedTableMain.c .\DLinkedList.c .\Person.c .\Table2.c
  > .\a.exe
  > 출력
  SSN: 900254 
  Name: Lee      
  Address: Seoul 
  
  SSN: 900139    
  Name: KIM      
  Address: Jeju  
  
  SSN: 900827
  Name: HAN
  Address: Kangwon

구현한 테이블 회고

구현한 테이블에 대해서 반성할 점이 있어 이것에 대해 알아보자.
(사소한 것이라고 생각할 수 있다.)

테이블 관련 삭제와 탐색 관련 함수를 다음과 같이 정의하였다.

Value TBLDelete(Table * pt, Key k)
{
    ....
    return NULL;	// 삭제할 대상이 존재하지 않는 경우
}

Value TBLSearch(Table * pt, Key k)
{
    ....
    return NULL;	// 찾는 대상이 존재하지 않는 경우
}

위에서 보이듯 삭제 또는 탐색의 결과로 값을 반환하도록 함수를 정의했다.
그리고 삭제 또는 탐색의 대상을 찾지 못하면 NULL을 반환하도록 정의했다.
그런데 이 NULL 반환이 문제가 되지 않기 위해서는 "반환되는 값, 테이블에 저장되는 값은 메모리의 주소 값이라고 가정하고 Value는 포인터 형으로 선언된다고 가정한다"라는 가정이 필요하다.

NULL은 일반적으로 "의미 없는 주소 값"을 뜻할 때 사용된다.
그런데 NULL은 그 자체로 정수 0이기 때문에 다른 용도로 사용할 경우 0이라는 의미를 지니는 데이터로 오해할 수 있다.
실제로 위의 두 함수가 반환하는 값이 int형이라면 같은 의미지만, Value를 포인터 형으로 선언하였기 때문에 같은 의미가 아니다.

따라서 구현한 테이블의 이러한 특성을 알고 있어 Value가 포인터 형으로 선언되어야 한다는 제약을 없애기 위해서는 어떻게 하면 좋을까?
그러기 위해서는 다음 두 가지를 고민해봐야 한다.

• 함수호출을 통해서 얻고자 하는 데이터를 어떻게 전달할 것인가?
• 함수호출의 성공여부를 어떻게 전달할 것인가?

함수의 반환 값 하나에 담으려 한 경우 괜찮은 경우도 있지만 그렇지 않은 경우가 있다.
예를 들어서 Value가 포인터 형이어야 한다는 제약사항을 없애기 위해서는 위의 두 가지 답변을 듣는 경로를 다음과 같이 나눠야 한다.

Value TBLDelete(Table * pt, Key k, Value * pv)
{
    ....
    return FALSE;	// 삭제할 대상이 존재하지 않는 경우
}

Value TBLSearch(Table * pt, Key k, Value * pv)
{
    ....
    return FALSE;	// 찾는 대상이 존재하지 않는 경우
}

이는 Value가 포인터 형이어야 한다는 제약사항을 없앨 목적으로 다시 정의한 함수다.
반환 값을 통해서 함수호출의 성공여부를, 매개변수를 통해서 삭제 또는 탐색 대상의 값을 얻도록 정의했다.
이를 통해서 Value가 주소 값이어야 한다는 제약사항도 사라지게 되었다.

---

<Review>

이번 테이블은 해쉬 함수까지는 괜찮았지만 연결 리스트 (앞에서 배운 내용)과 연결지어 나올 땐 약간 이해하기 어려웠다.
코드를 따라 치면서도 어떤 걸 가리키고 있는지 머리로 잘 그려지지 않았다.
이 부분에 대해서는 손으로 직접 그려가며, 예시를 생각하면서 다시 한번 이해해봐야 하는 부분인거 같다.

드디어 마지막 Chapter 하나를 남겨두고 있다.
코딩 공부을 하면 할수록 내가 알고 있는 것도 잘 알고 있는지 의문이 들고 있는데,,,
코딩을 정말 좋아하고 열정적으로 공부하는 사람들의 마음가짐,
내가 초반에 코딩 공부를 시작하게 된 이유와 마음가짐을 다시 한번 돌아봐야겠다.