ReLU를 사용하는 RNN에서 vanishing 혹은 exploding gradient없이 학습하기 위해 recurrent 초기 가중치 행렬로 positivie definite identity matrix를 활용하는 np-RNN에 관한 논문입니다.
[Abstract]
최근 연구에서 long range temporal dependenciy를 포함한 sequence learning 문제 해결을 위해 RNN(Recurrent Neural Network)을 성공적으로 학습할 수 있는 중요한 진전이 있었습니다. 이러한 진전은 3가지 측면에서 이루어 졌습니다.
- 정교화된 최적화 방법을 포한한 알고리즘적인 발전
- 복잡한 hidden layer와 특별한 recurrent layer connection을 포함한 network design의 발전
- 가중치 초기화 방법의 변화
해당 논문에서는 RNN의 recurrent 가중치의 가중치 초기화에 identity matrix를 활용한 것에 집중하였습니다. 이러한 초기화는 ReLU를 활용한 hidden node를 타깃으로 제안되었습니다.
1. Introduction
RNN은 hidden node 사이에서 순환연결을 갖고 있는 neural network입니다. 순환연결은 RNN이 memory를 encode할 수 있도록 해주었고, 성공적으로 학습된다면 sequence learning에 적합하다고 볼 수 있습니다. BPTT(Back-Propagation through time)과 같은 SGD를 사용하여 rnn을 학습하는 것은 어려운 일이었습니다. 초창기에는 vasnishing gradient 혹은 exploding gradient 문제에 빠져 long range temporal dependency에 문제를 겪었습니다.
RNN 학습의 어려움을 극복하기 위해 몇몇 방법들이 제안되었습니다. 이런 방법들은 3가지 범주로 분류할 수 있습니다.
- 정교화된 최적화 기술을 활용한 알고리즘적은 발전 : HF(Hessian-Free) 최적화 방법은 low gradient와 curvature 방향으로 가중치 공간에서 크게 움직이는 방식입니다.
- LSTM(Long Short Term Memory)로 대표되는 Network design의 발전 : LSTM은 기본 RNN에서 tanh, sigmoid와 같은 단조 비선형함수를 long range range에 대해 정보를 전달할 수 있고 효율적으로 continuous value를 저장할 수 있는 memory unit으로 교체한 것입니다. 더욱 최근에는 기본 RNN의 변형 중 하나인 CW-RNN(ClockWork RNN)이 제안되기도 하였습니다. CW-RNN은 hidden layer를 나누어 개별 module로 만들고 각각을 서로 다른 clock speed로 동작하게 만들어 vanishing and exploding gradient 문제를 해결하였습니다.
- 가중치 초기화 : 과거의 한 연구에서 ReLU로 구성된 RNN들의 long-range dependence 문제를 해결할 수 있는 단순한 방법을 제안하였습니다. 과거 연구 저자들은 recurrent 가중치 matrix로 Identity matrix를 사용하였습니다. 과거 연구 저자들은 이러한 RNN을 IRNN(Identity-RNN)이라 하였습니다. IRNN의 기본 아이디어는 어떠한 input도 존재하지 않는다면 ReLU로 이루어지고 identity 가중치 matrix로 초기화된 RNN은 모두 동일하게 유지될 것이라는 점입니다.
해당 논문에서는 Mobie computing platform에 RNN을 적용하기 위해 low memory 환경이 중요했기 때문에 IRNN의 결과에 흥미를 가졌습니다. 따라서 IRNN 자체와 IRNN에서 identity 가중치 matrix의 중요성을 dynamical system 관점으로 포커스를 맞추었습니다.
해당 논문에서는 input에 대한 hidden node dynamics의 민감도가 RNN의 성공여부에 영향을 미친다고 가정하였습니다. 이러한 가정 하에서 해당 논문은 ReLU로 구성된 RNN의 새로운 가중치 행렬로 normalized-positive definite weight matrix를 제안합니다. 이런 RNN을 np-RNN으로 명명하고, IRNN과 IRNN의 scaled version인 i-RNN보다 좋은 성능을 갖는다는 것을 보입니다.
2. Dynamical systems perspective on RNNs
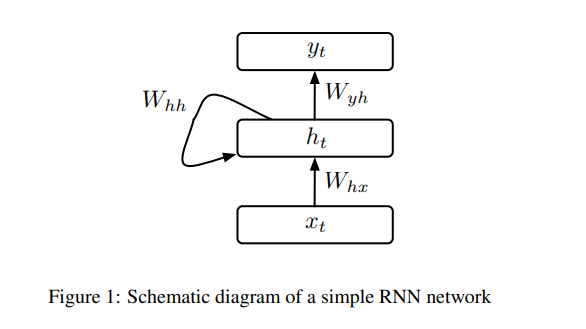
sRNN(Simple RNN)은 input layer와 recurrent connection이 있는 hidden layer 그리고 output layer로 구성되었습니다. Input X={x_0 ~ x_T}가 주어졌을 때 sRNN은 input x_t로부터 예측값 y_t를 만들어냅니다. Input과 output 사이에는 M unit hidden layer가 있으며 hidden layer에는 input sequence의 과거 정보들이 저장되어 있습니다. sRNN은 X를 input으로 하여 output Z의 추정치 Y를 아래 식들을 반복하여 얻습니다.

sRNN의 objective function O(theta)는 theta들이 parameter들의 집합을 나타낼 때 다음과 같이 나타낼 수 있습니다.

IRNN은 sRNN에서 약간의 수정을 해준 모델입니다.
- f는 ReLu를 활용합니다.
- Hidden layer 가중치 W_hh는 identity matrix로 초기화되고 bias term은 0으로 설정합니다. BPTT 알고리즘은 아래와 같습니다.

IRNN의 구성을 dynamical system 관점으로 이해하기 위하여 ReLU를 사용한 2개의 hidden node로 구성된 sRNN의 단순한 예제를 생각해봅시다. sRNN은 zero input을 갖고 모든 bias들은 0으로 세팅이 되어있다고 합시다. 더 나아가 recurrent weight matrix W_hh가 positive definite라고 합시다. 이 때 hidden node의 dynaics는 다음과 같은 식으로 주어집니다.
아래 그림은, 위 식 (8)에서 recurrent weight matrix의 eigenvalue lamda 값에 따라 hidden node의 dynamical system을 그린 것입니다.

해당 논문에서는 위의 그림에서 (c) case(one eigenvalue is unitiy and the other eigenvalue is less than 1)의 가중치 행렬을 활용할 때 sRNN이 vanishing or exploding gradient 문제에 빠지지 않고 학습이 잘 될 수 있다고 가정합니다.
위 그림의 결과를 바탕으로 해당 논문에서는 rucurrent weight matrix W_hh를 고르기 위해 아래의 식을 제안하였고 이를 만족하는 RNN을 np-RNN이라 하였습니다.

R은 표준정규분포에서 iid 조건을 만족하면서 뽑인 값들로 이루진 standard normal matrix이고 lamda(X)는 행렬 X의 모든 eigenvalue들의 집합입니다. 식 (9)는 W_hh가 positive definite이면서 가장 큰 eigenvalue가 1이고 나머지 eigenvalue들은 1보다 작은 값을 가질 수 있도록 해줍니다.
3. Experiments

모든 RNN들은 100 hidden nodes의 하나의 hidden layer를 사용합니다. np-tanhRNN을 제외한 모든 RNN들은 ReLU를 사용합니다. non recurrent weigth matrix W_hx의 값들은 평균이 0이고 분산이 1/N인 정규분포에서 추출된 값들을 원소로 갖습니다. 과거 연구에 기반하여 W_bx를 아래 값을 갖는 factor alpha로 scaling 해줍니다.

non-recurrent weight matrix W_hy 역시 평균이 0이고 분산이 2/(fan_in+fan_out)인 정규분포에서 iid로 뽑힌 값들을 원소로 갖습니다.
모든 RNN들은 SGD with BPTT를 통해 학습됩니다.
- The Addition problem : RNN의 long-term dependency 학습 power를 평가할 수 있는 task입니다. 2개의 행을 갖는 matrix에서 첫 번째 행벡터는 0과 1 사이의 실수 값을 갖고 두 번째 행벡터는 2개의 원소만 1이고 나머지는 모두 0의 값을 갖습니다. 해당 task는 두 번째 행벡터의 원소가 1인 index의 첫 번째 행벡터 원소들의 합을 구하는 것입니다.
- The multiplication problem : the apddition problem과 동일한 setting에서 덧셈 대신 곱셈을 수행합니다.
- MNIST classification with sequential presentation of pixels : MNIST 숫자 분류 task
- Action recognition benchmark : 2~10초의 짧은 비디오 클립을 101개의 class 중 하나로 분류하는 task
4. Result
4.1 Addition Problem

4.2 Multiplication Problem

4.3 MNIST Classification with sequential presentation of pixels

4.4 Action recognition benchmark


5. Conclusion
해당 논문에서는 ReLU로 구성된 RNN의 recurrent weight matrix가 identity matrix일 경우를 dynamical system 관점에서 제시하였습니다. 해당 논문에서는 identity weight matrix 초기화로부터 나온 sensitivity of hidden nodes to input perturbation가 IRNN의 성공적인 학습을 위한 hyperparameter 선택을 민감하게 만들어준다고 가정하였습니다. 해당 논문에서는 대안으로 사용할 수 있는 가중치 초기화 방법을 제안하였습니다. 해당 방법은 가중치 초기화 행렬로 normalized positive-definite weight 행렬을 사용하는 것으로 dynamics를 1차원 manifold로 줄여 sensitivity of hidden nodes to input perturbatio를 줄여주었습니다.