[JAVA] 자료형의 종류, 연산자

mingsso·2024년 3월 5일

Java-Kotlin

목록 보기

2/17

1️⃣ 자바의 기본 자료형

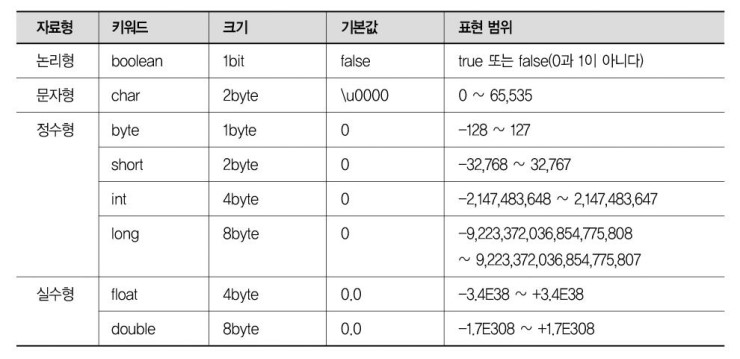
정수

자바는 정수형 연산은 int형으로 진행함 -> 연산을 동반하는 상황에서는 int로 선언
그냥 정수를 쓰면 int형으로 인식함
But, 자바는 byte형과 short형 정수의 표현방법은 제공하지 않기 때문에 초기화 허용

long num = 3147483647;   // 컴파일 오류 발생 
byte num1 = 5;   // 허용
short num2 = 25;   // 허용

long형 정수로 초기화하기 위해서는 숫자의 끝에 문자 L 또는 l을 붙여야 함

System.out.println(3147483647L + 3147483648L);

단위가 큰 수의 표현 및 인식에 도움을 주기 위해 언더바 삽입 가능

int num = 100_000_000;

정수형 상수의 표현 방법

// 10진수로 int형 정수 표현
int num = 11 + 22 + 33;

// 2진수로 int형 정수 표현: 2진수 표현 앞에 0B 또는 0b 삽입
int num205 = 0B1101101;

// 8진수로 int형 정수 표현: 숫자 앞에 0 삽입
int num = 011 + 022 + 033;

// 16진수로 int형 정수 표현: 숫자 앞에 0x 또는 0X 삽입
int num = 0x11 + 0x22 + 0x33;

실수

float와 double의 차이는 정밀도
-> float는 소수점 이하 6자리까지는 오차가 발생하지 않고, double은 소수점 이하 15자리까지 오차가 발생하지 않음

실수형 상수는 double형으로 인식됨

double pi = 3.1415;

float형 실수를 표현하고 싶다면 f 또는 F를 붙이면 됨

System.out.println(3.004999f + 2.0004999f);

문자

문자를 char형 변수에 저장할 때 실제 저장되는 것은 해당 문자의 유니코드 값임

이스케이프 시퀀스 : 유니코드 문자들 중 키보드로 입력하기 어려운 문자의 표현을 위함

\b : 백스페이스 문자
\t : 탭 문자
\\ : 백슬래시 문자
\' : 작은따옴표 문자
\" : 큰따옴표 문자
\n : 개행 문자
\r : 캐리지 리턴 문자 (커서를 왼쪽 끝으로 이동시킴)

System.out.println("AB" + '\r' + 'C');   // CB
System.out.println("1$에 0.88" + '\u20AC');   // 1$에 0.88€

2️⃣ 정수의 표현 방식

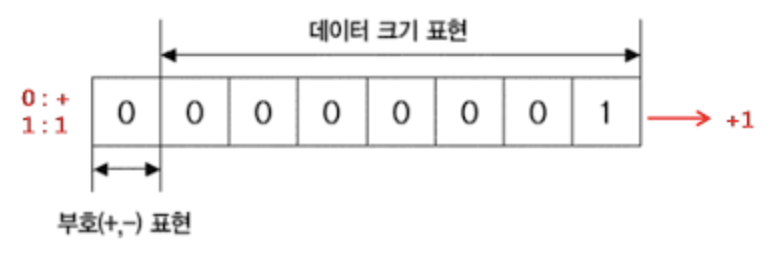
이때 음의 정수 -1을 위의 방식대로 10000001로 표시하면,
00000001 + 10000001 = 10000010
위 연산의 경우 어떠한 방식으로 해석을 하건 0이 될 수 없음 -> 음의 정수는 다른 방식으로 표현해야 함

양의 정수의 이진수 표현에 2의 보수를 취한 결과를 음의 정수로 표현한다

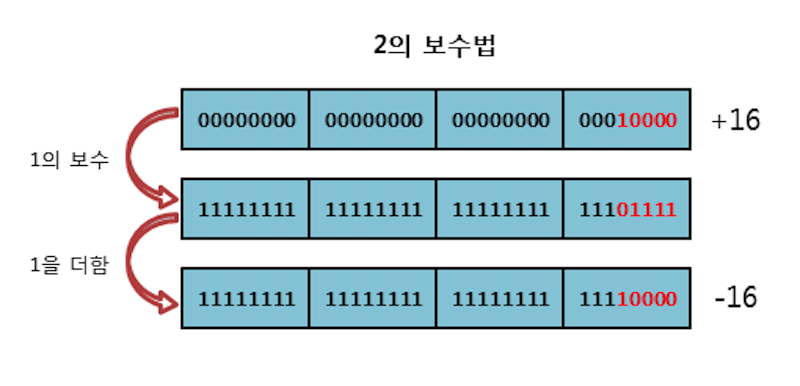
3️⃣ 실수의 표현 방식

정수는 오차 없이 표현이 가능하지만, 광대한 실수를 오차 없이 표현하는 것은 불가능함
-> 정밀도를 낮추고 대신에 표현할 수 있는 값의 범위를 넓히자

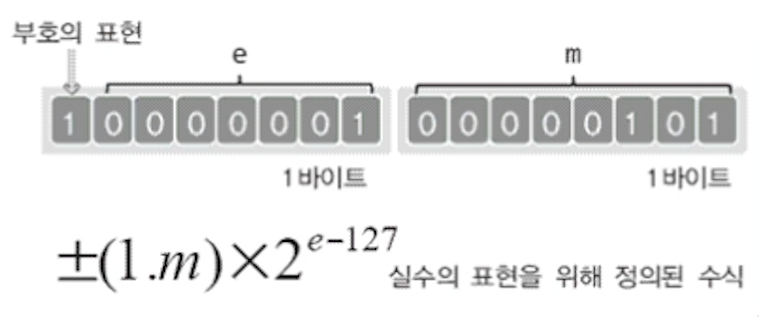
예를 들어 부호 비트에는 0을, e에는 00000을, m에는 0000000001을 넣으면,
+(1.1)x2^-127이 되며, 이 값은 약 6.46521893 x (10의 -39승)임

하지만 위의 표현 방식으로는, 6.4652...보다 아주 조금 작거나 큰 수는 표현하지 못함
즉 상대적으로 표현하는 대부분의 값에는 오차가 존재하게 됨

double num1 = 1.0000001;   // 1.0000001에 최대한 가까운 수가 만들어짐

4️⃣ 연산자

기본 연산자

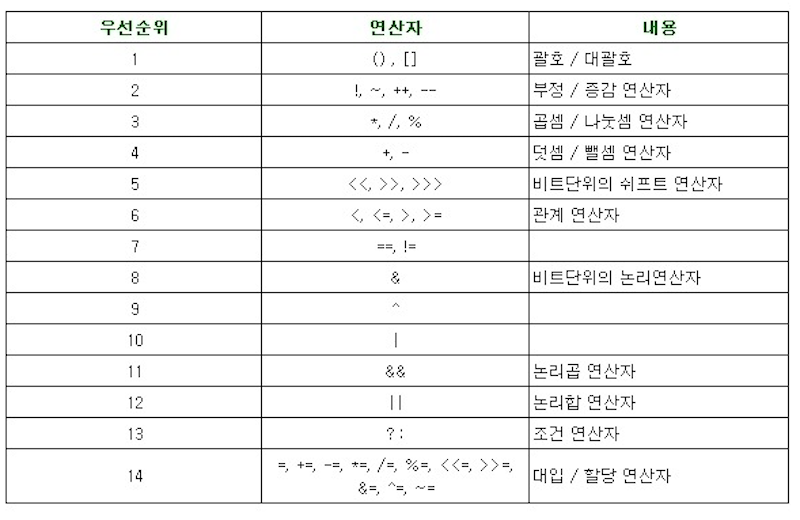
복합 대입 연산자를 사용하면 형 변환 알아서 해줌

num = (short)(num + 77L)   // 형 변환 필요
num += 77L   // 형 변환 불필요

비트 연산자 (연산 결과는 int형)
- & : 비트 단위로 AND 연산
- | : 비트 단위로 OR 연산
- ^ : 비트 단위로 XOR 연산
- ~ : 피연산자의 모든 비트를 반전시켜서 얻은 결과를 반환

비트 시프트 연산자 (피연산자의 모든 비트 열을 왼쪽 또는 오른쪽으로 이동)
- << : 피연산자의 비트 열을 왼쪽으로 이동, 이동에 따른 빈 공간은 0으로 채움
- >> : 피연산자의 비트 열을 오른쪽으로 이동, 이동에 따른 빈 공간은 음수의 경우 1, 양수의 경우 0으로 채움
- >>> : 피연산자의 비트 열을 오른쪽으로 이동, 이동에 따른 빈 공간은 0으로 채움

num = 2;   // 00000010
System.out.print((byte)(num << 1));   // 00000100 (2배 증가)

num = 8;   // 00001000
System.out.print((byte)(num >> 1));   // 00000100 (절반으로 줄어듦)