1️⃣ 풀이 방법
최단 길이의 개수가 몇 개인지? -> DP
DP vs 그리디 -> 지금 이 데이터를 포기함으로써 나중에 이득을 보게 될 수 있는가? 있으면 그리디, 아니면 DP..? 이게 맞나..?
- 규칙 찾기
- 메모라이제이션
- bottom-up 방식 = 주로 아래, 오른쪽으로만 이동하는 문제에서 이중 for문 이용해 푸는 경우 많음
+) 백준 파이프 옮기기 1
https://www.acmicpc.net/problem/17070
파이프를 board의 맨 아래 오른쪽 칸으로 옮기는 방법의 개수 구하기
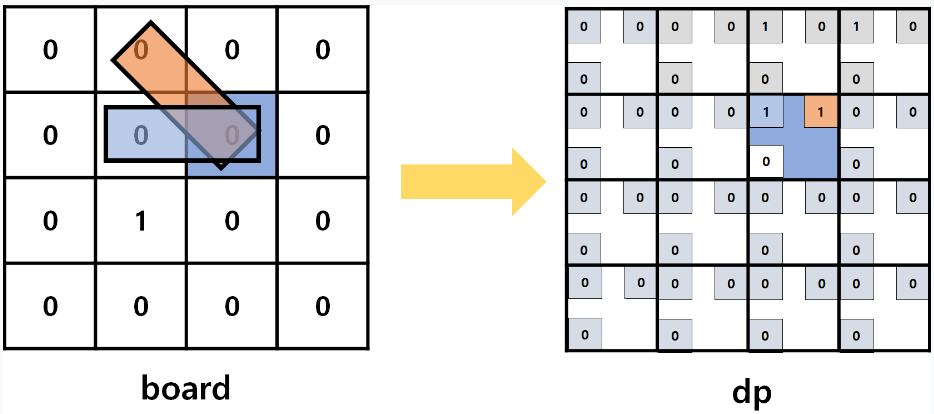
for i in range(1, n):
for j in range(1, n):
if home[i][j] == 0:
dp[i][j][0] += (dp[i][j-1][0] + dp[i][j-1][2])
dp[i][j][1] += (dp[i-1][j][1] + dp[i-1][j][2])
if home[i][j] == 0 and home[i-1][j] == 0 and home[i][j-1] == 0:
dp[i][j][2] += (dp[i-1][j-1][0] + dp[i-1][j-1][1] + dp[i-1][j-1][2])
- dp[인덱스][결과값] = 값의 유무 0과 1로 표시
-> 리스트 순서 지켜야 하는 문제, 리스트에서 뭔가 더하고 빼며 최대/최소값을 구해야 하는 문제
+) 백준 1학년
https://www.acmicpc.net/problem/5557
"8 3 2 4 8 7 2 4 0 8 8"에서 등식 "8+3-2-4+8-7-2-4-0+8=8"을 만드는 등 리스트에 덧셈과 뺄셈을 적절히 넣어 만들 수 있는 올바른 등식의 개수 출력
이때 중간에 나오는 수는 모두 0 이상 20 이하임
# dp[a][b] = 가능한 경우의 수(a번째까지의 수를 사용하여 b가 나올 수 있는)
dp = [[0] * 21 for _ in range(n)]
dp[0][arr[0]] += 1
for i in range(1, n-1):
for j in range(21):
if dp[i-1][j]:
if j + A[i] <= 20:
dp[i][j+A[i]] += dp[i-1][j]
if j - A[i] >= 0:
dp[i][j-A[i]] += dp[i-1][j]
print(dp[n-2][A[n-1]])
- 스티커 떼는 문제
for i in range(2, n):
board[0][i] += max(board[1][i-1], board[1][i-2])
board[1][i] += max(board[0][i-1], board[0][i-2])
print(max(board[0][n-1], board[1][n-1]))
sticker와 메모라이제이션 리스트를 따로 만드는 게 포인트!
def solution(sticker):
# 스티커가 1개일 경우
if len(sticker) == 1:
return sticker[0]
# 1. 맨 앞 스티커를 떼는 경우
table = [0 for _ in range(len(sticker))]
table[0] = sticker[0]
table[1] = table[0]
for i in range(2, len(sticker)-1):
table[i] = max(table[i-1], table[i-2] + sticker[i])
value = max(table)
# 2. 맨 앞 스티커를 떼지 않는 경우
table = [0 for _ in range(len(sticker))]
table[0] = 0
table[1] = sticker[1]
for i in range(2, len(sticker)):
table[i] = max(table[i-1], table[i-2] + sticker[i])
return max(value, max(table))
- DP + DFS
# 1) 왼쪽 위에서 오른쪽 아래로 이동할 때 항상 내리막길로만 이동하는 경로의 개수
def dfs(y, x):
if y == (m - 1) and x == (n - 1):
return 1
if dp[y][x] != -1:
return dp[y][x]
dp[y][x] = 0
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < m and height[y][x] > height[ny][nx]:
dp[y][x] += dfs(ny, nx)
return dp[y][x]
dfs(0, 0)
print(dp[0][0])
# 2) 오르막길로 이동할 수 있을 때 이동할 수 있는 칸의 최댓값 구하기
def dfs(y, x):
if dp[y][x] != 0:
return dp[y][x]
dp[y][x] = 1 # 1칸(y,x)는 이동했으니까 1
for i in range(4):
ny = y + dy[i]
nx = x + dx[i]
if 0 <= ny < n and 0 <= nx < n and boo[y][x] < boo[ny][nx]:
dp[y][x] = max(dp[y][x], dfs(ny, nx) + 1)
return dp[y][x]
answer = 0
for i in range(n):
for j in range(n):
answer = max(answer, dfs(i, j))
- 냅색 알고리즘
- 위상정렬
- 연쇄 행렬 곱셈
2️⃣ 문제 풀이
* LIS (가장 긴 증가하는 부분 수열)
# 가장 긴 증가하는 부분 수열
dp = [1] * n
for i in range(n):
for j in range(i):
if A[j] < A[i]:
dp1[i] = max(dp1[i], dp1[j] + 1)
# 가장 긴 감소하는 부분 수열
dp2 = [1] * n
for i in range(n-1, -1, -1):
for j in range(n-1, i, -1):
if A[j] < A[i]:
dp2[i] = max(dp2[i], dp2[j] + 1)
# 가장 긴 바이토닉 부분 수열 -> 10 20 30 25 20
dp = [0] * n
for i in range(n):
dp[i] = dp1[i] + dp2[i] - 1* 백준 평범한 배낭 (🥇5) -> 0-1 배낭문제
https://www.acmicpc.net/problem/12865
준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가진다. 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 배낭에 넣을 수 있는 물건들의 가치의 최대값?
-> 우선순위 큐 문제는 물건 한 개만 넣을 수 있는 가방 여러 개, 냅색 문제는 여러 개의 물건을 넣을 수 있는 가방 1개
# dp[n][k] = n번째 물건까지 살펴보았을 때, 무게가 k인 배낭의 최대 가치
dp = [[0] * (k + 1) for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, k+1):
w = thing[i][0]
v = thing[i][1]
# 현재 배낭의 허용 무게보다 넣을 물건의 무게가 더 크다면, 이전 배낭 그대로
if j < w:
dp[i][j] = dp[i-1][j]
else:
# max(현재 넣을 물건의 무게만큼 배낭에서 빼고 현재 물건 넣음, 이전 배낭 그대로)
dp[i][j] = max(v + dp[i-1][j-w], dp[i-1][j])+) 백준 앱 - https://www.acmicpc.net/problem/7579
* 백준 동전 분배 (🥇3) -> 0-1 배낭문제
https://www.acmicpc.net/problem/1943
원장 선생님께서 윤희와 준희에게 N가지 종류의 동전을 각각 몇 개씩 주셨을 때, 그 돈을 반으로 나눌 수 있는지 없는지 판단
# 홀수는 반으로 나눠질 수 없으므로 굳이 확인 안 해도 됨
if total % 2 == 1:
print(0)
continue
total //= 2
dp = [True] + [False] * total # dp[n] = 주어진 동전들로 n원을 만들 수 있는가
answer = 0
for i in range(n):
k, c = coin[i] # k는 동전의 종류(500원), c는 해당 동전의 개수(1개)
for j in range(total, k-1, -1): # 나눈 금액~500원
# j-k가 True라면, j원도 지불할 수 있음(k원 동전이 하나 생긴 것)
if dp[j-k]:
for t in range(c): # 마찬가지로 j+k*t원도 지불할 수 있음
if j + k * t <= total:
dp[j+k*t] = True
else:
break
- dp[0] = True
- total부터 역순으로 확인
* 백준 행렬 곱셈 순서 (🥇3)
https://www.acmicpc.net/problem/11049
for size in range(1, n): # 분할된 그룹의 크기
for start in range(n-size): # 크기가 size인 그룹의 모든 경우의 수
end = start + size
rst = float('inf')
for cut in range(start, end):
rst = min(rst, dp[start][cut] + dp[cut+1][end] +
arr[start][0] * arr[cut][1] * arr[end][1])
dp[start][end] = rst* 백준 퇴사 (🥈3)
https://www.acmicpc.net/problem/14501
각각의 상담은 상담을 완료하는데 걸리는 기간 Ti와 상담을 했을 때 받을 수 있는 금액 Pi로 이루어져 있음. 상담을 적절히 했을 때 얻을 수 있는 최대 수익?
-> 배낭 문제와 유사하지만 한도가 없음
dp = [0 for _ in range(n+1)]
for i in range(n-1, -1, -1):
if consult[i][0] + i <= n: # 날짜를 초과하지 않을 경우
# max(상담 금액 + dp[상담 끝마친 시간], 해당 상담을 하지 않았을 때)
dp[i] = max(consult[i][1] + dp[i+consult[i][0]], dp[i+1])
else: # 날짜를 초과할 경우
dp[i] = dp[i+1]
print(dp[0])* 백준 1, 2, 3 더하기 5 (🥈2)
https://www.acmicpc.net/problem/15990
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 3가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 하며, 같은 수를 두 번 이상 연속해서 사용하면 안된다.
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수
dp = [[0, 0, 0] for _ in range(100001)] # [1로 끝나는 방법 수, 2로 끝나는 방법 수, 3으로 끝나는 방법 수]
dp[1] = [1, 0, 0] # 1
dp[2] = [0, 1, 0] # 2
dp[3] = [1, 1, 1] # 2+1, 1+2, 3
for i in range(4, 100001):
dp[i][0] = (dp[i-1][1] + dp[i-1][2]) % 1000000009
dp[i][1] = (dp[i-2][0] + dp[i-2][2]) % 1000000009
dp[i][2] = (dp[i-3][0] + dp[i-3][1]) % 1000000009* 프로그래머스 N으로 표현 (Level 3)
https://school.programmers.co.kr/learn/courses/30/lessons/42895
N과 사칙연산만을 사용해서 number을 표현할 수 있는 방법 중 N 사용횟수의 최솟값
최솟값이 8보다 크면 -1을 리턴함
12 = (55 + 5) / 5
dp = [set() for _ in range(9)]
for i in range(1, 9):
dp[i].add(int(str(N)*i))
for j in range(1, i):
for op1 in dp[j]:
for op2 in dp[i-j]:
dp[i].add(op1 + op2)
dp[i].add(op1 - op2)
dp[i].add(op1 * op2)
if op2 != 0:
dp[i].add(op1 // op2)
if number in dp[i]:
return idp = [set() for _ in range(9)] 이런 식으로 사용할 수도 있음
3중 for문 사용해서 op1, op2 고르는 부분 집중
