그래프

mingsso·2023년 4월 12일
BFS
0

Algorithm

목록 보기
11/35

1️⃣ 개념

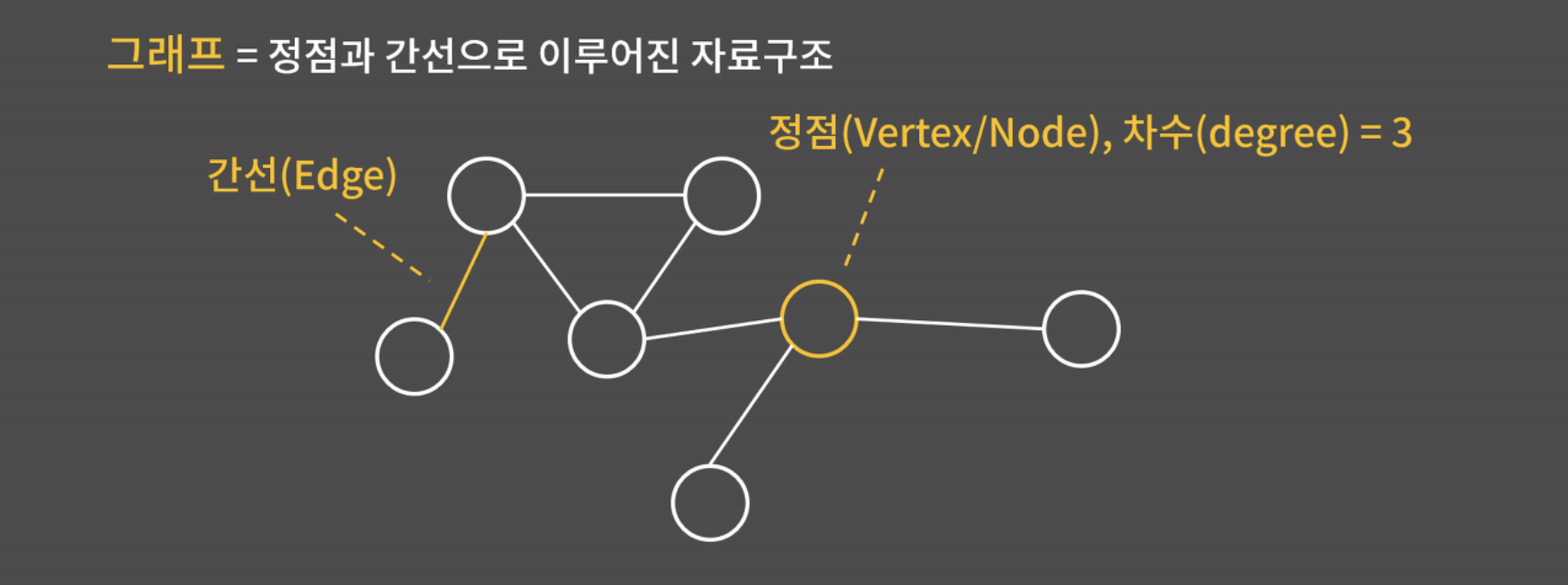
그래프의 정의 G(V, E)

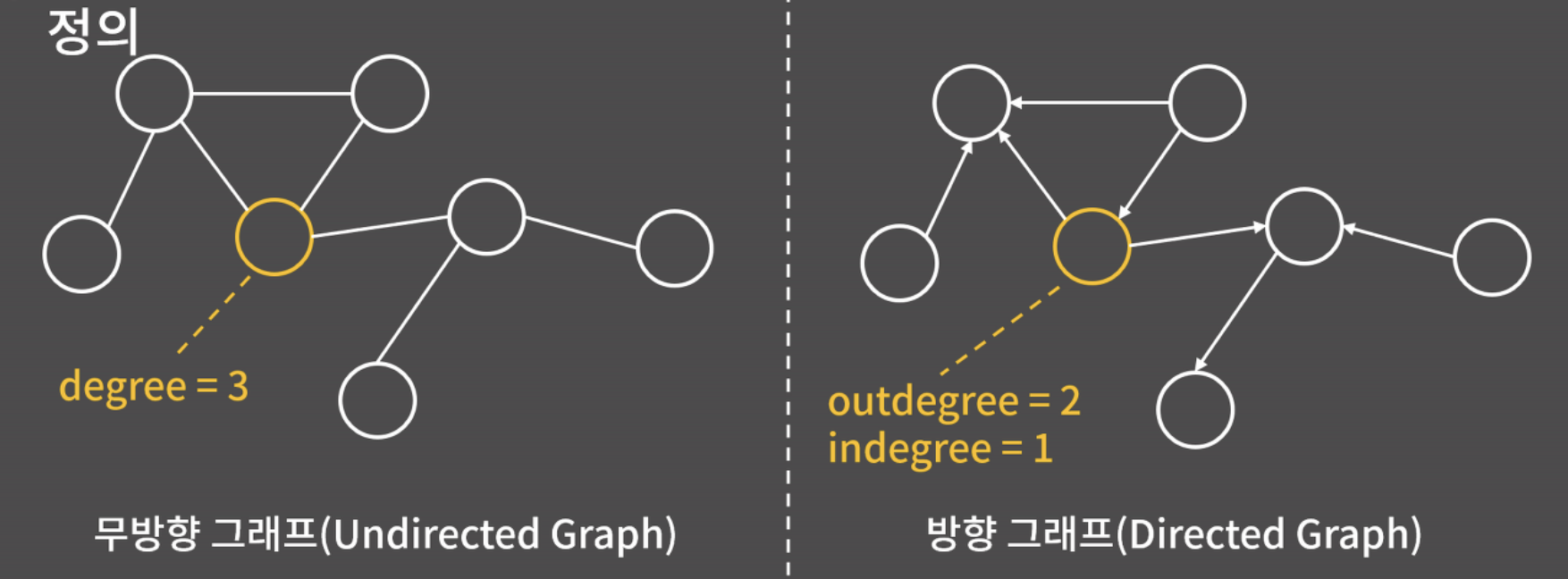
  1. 방향 그래프(유향 그래프) / 무향 그래프

    ​
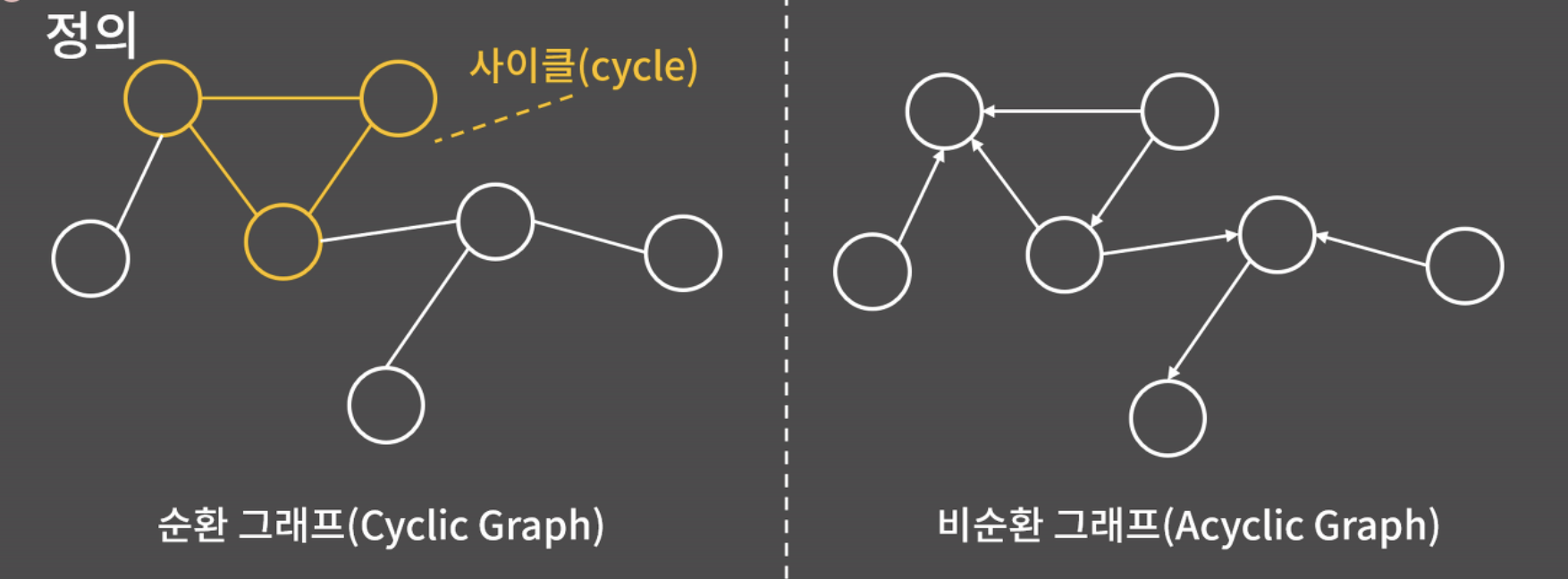
  2. 순환 그래프 / 비순환 그래프
    사이클이 하나라도 있으면 순환 그래프

    ​
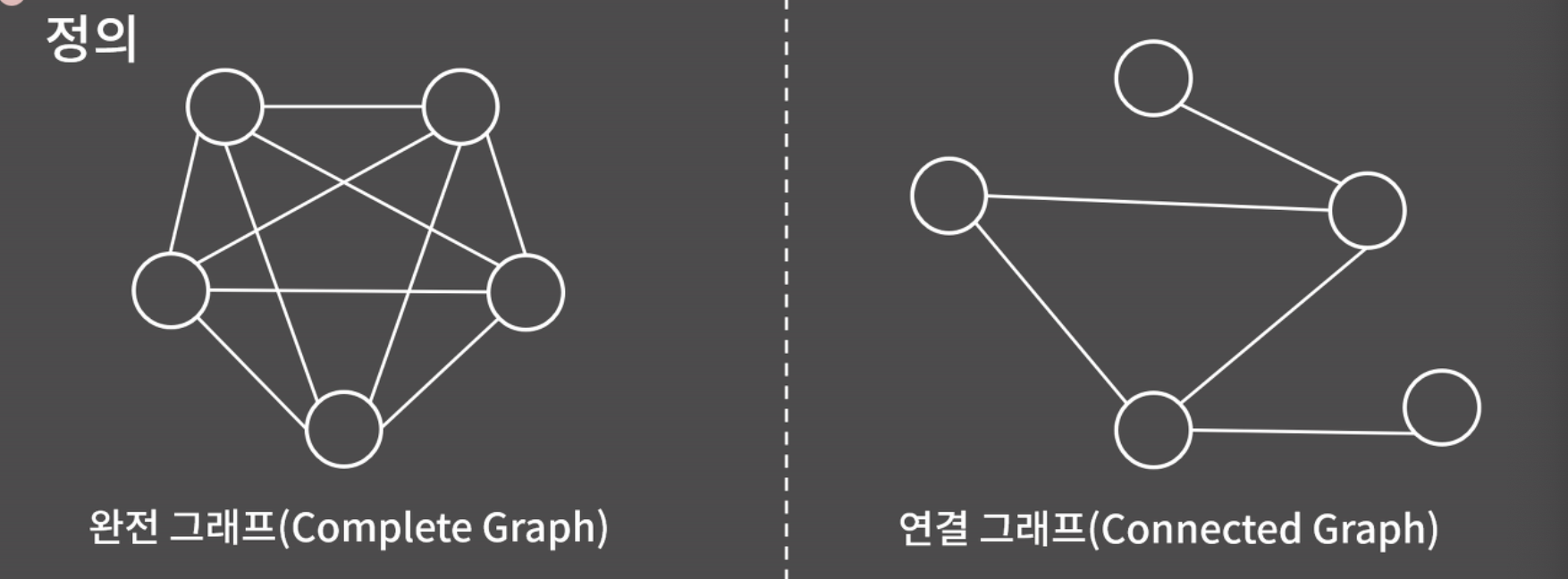
  3. 완전 그래프 / 연결 그래프
  • 완전 그래프 - 모든 서로 다른 두 정점 쌍이 간선으로 연결된 그래프
  • 연결 그래프 - 임의의 두 정점 사이에 경로가 항상 존재하는 그래프

    ​
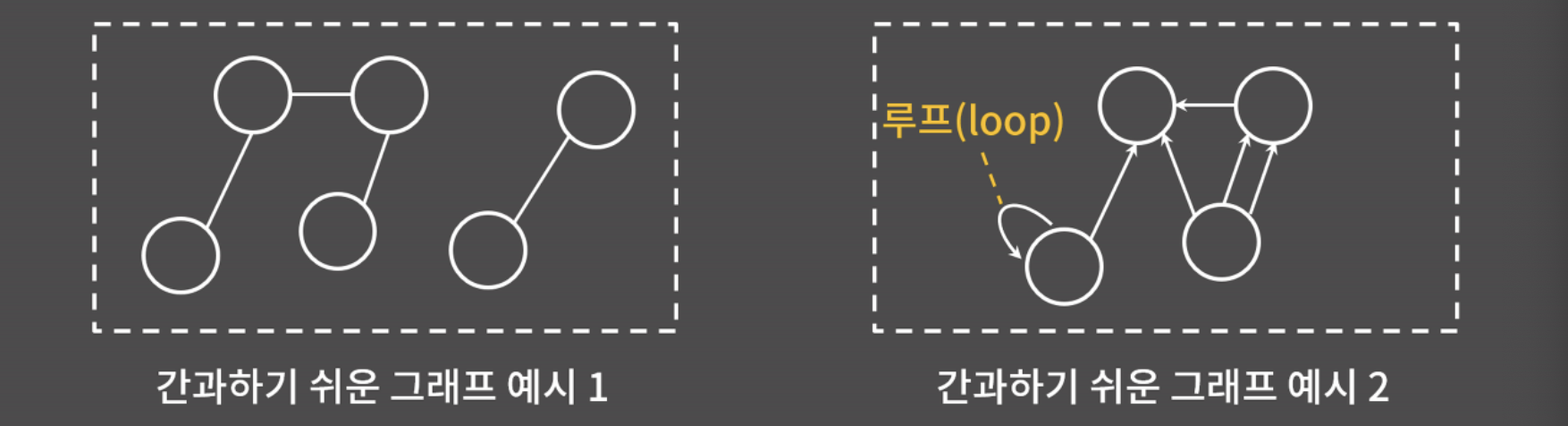
  1. 간과하기 쉬운 그래프
  • 루프 - 한 정점에서 시작해 같은 정점으로 들어오는 간선
  • 단순 그래프 - 두 정점 사이의 간선이 1개 이하이고, 루프가 존재하지 않는 그래프



그래프의 표현 방법

  1. 인접 행렬 이용
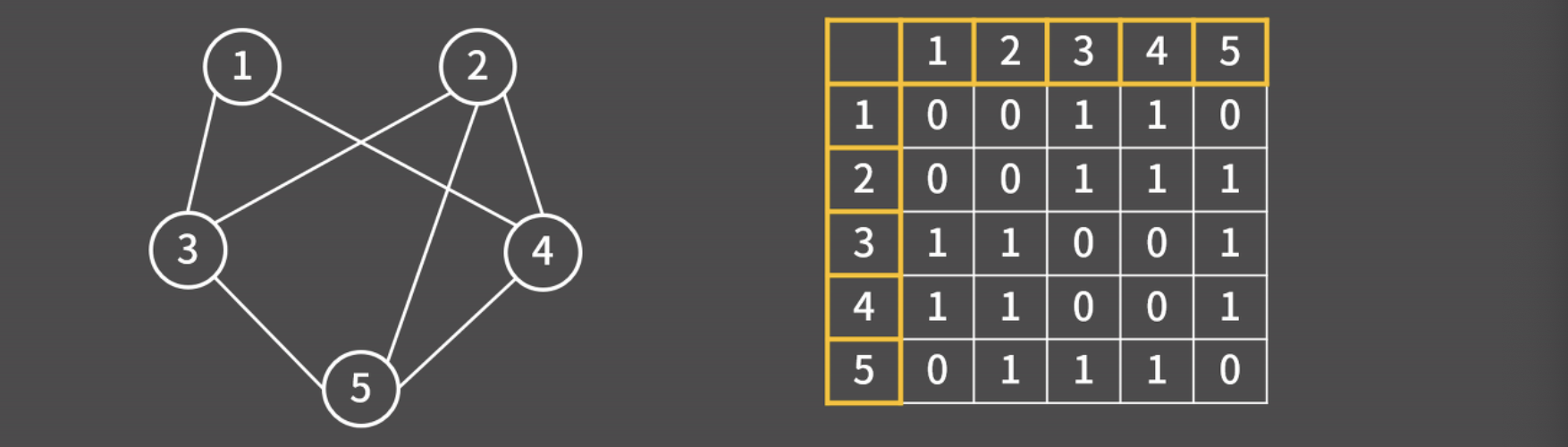
  • 연결된 두 정점에는 1을, 연결되지 않은 두 정점에는 0을 줌
  • 무방향 그래프 = 왼쪽 위와 오른쪽 아래를 연결하는 대각선에 대해 대칭인 형태
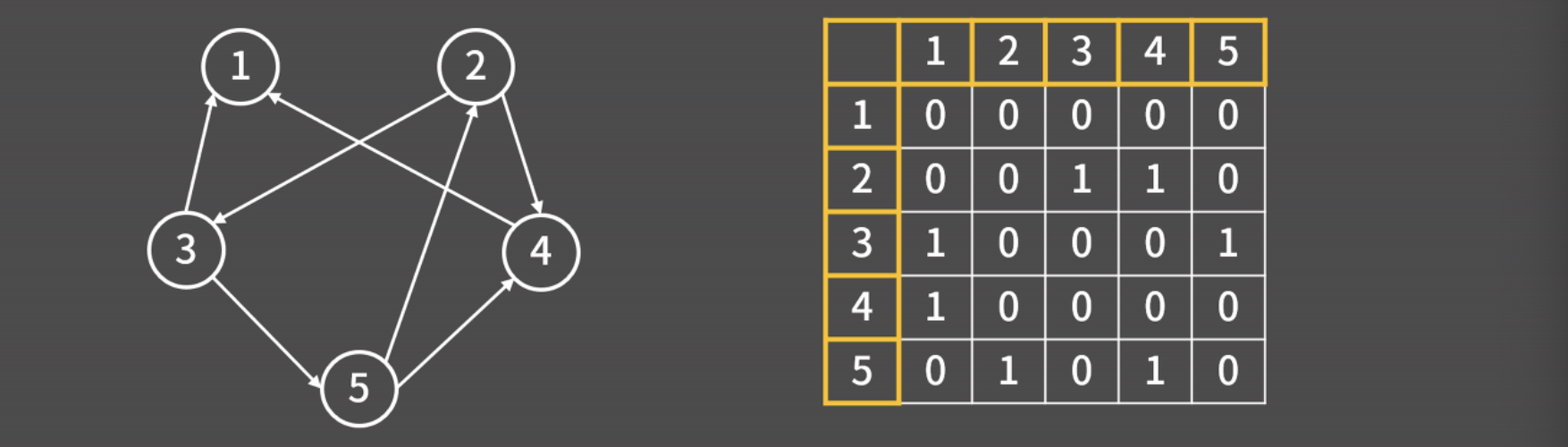
  • (2, 3)이 1이라는 의미는 2에서 3으로 가는 간선이 있다는 의미

​

  • 인접 행렬로 그래프를 나타내면 정점이 V개이고 간선이 E개일 때 어떤 두 점이 연결되어 있는지를 O(1)만에 알 수 있음
  • 가로와 세로가 각각 V인 2차원 배열이 필요하니 O(V^2)의 공간을 필요로 함
  • 어떤 점에 연결되어 있는 모든 정점의 목록을 알아내고 싶을 때에도 개수와 무관하게 시간복잡도가 O(V)임


  1. 인접 리스트 이용
    인접 행렬과 비교했을 때 정점이 많고 간선은 상대적으로 적은 상황에서 공간을 절약할 수 있음
  • 인접 리스트에서는 O(V+E)의 공간이 필요함
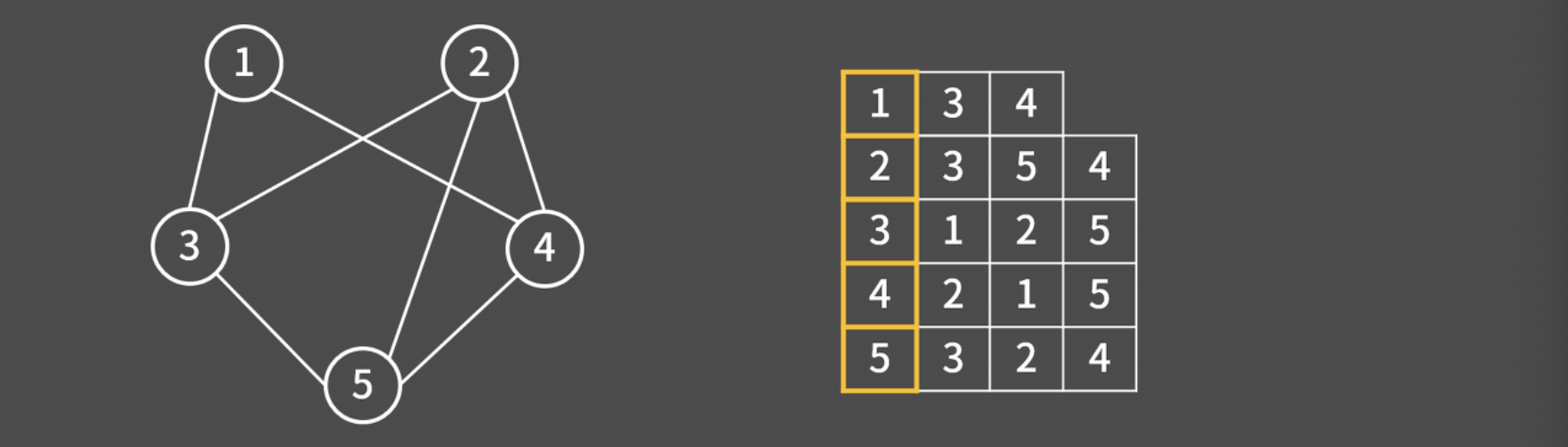
  • V개의 리스트를 만들어 자신과 연결된 정점을 넣으면 됨


  1. 인접 행렬 vs 인접 리스트



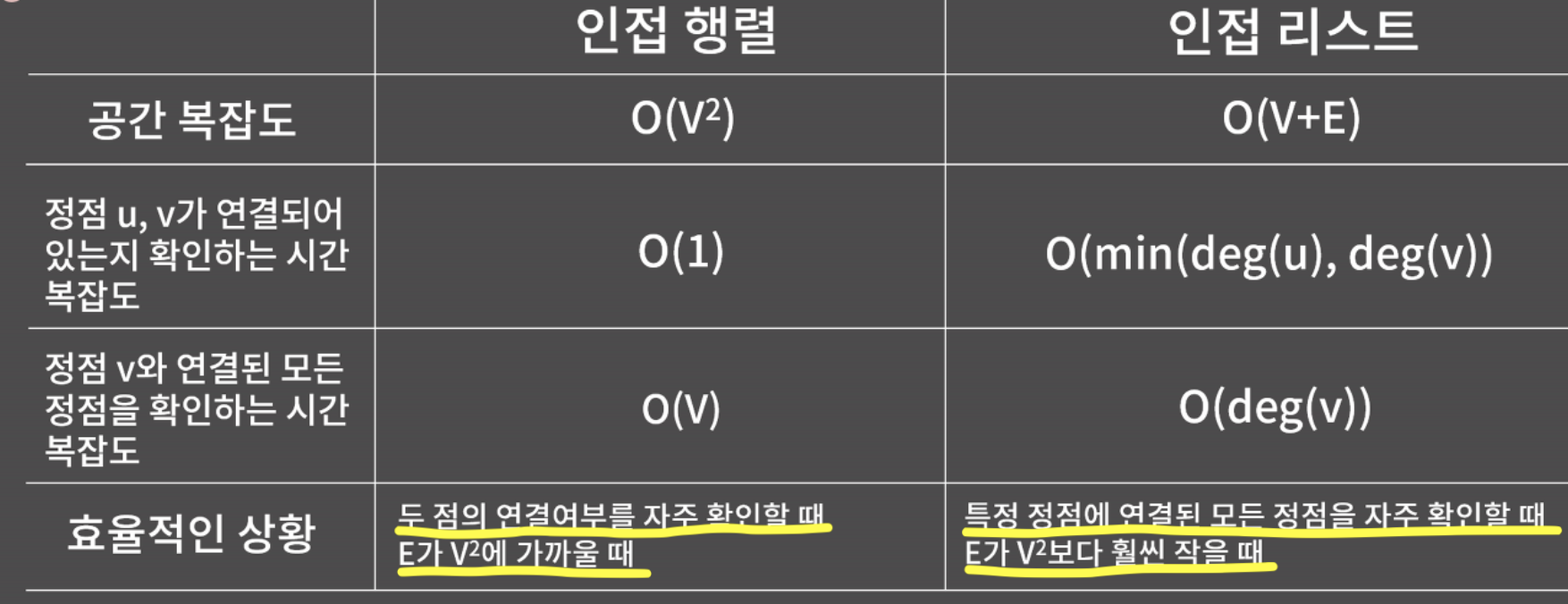
❓그래프의 탐색 알고리즘
그래프의 모든 정점들을 특정한 순서에 따라 방문하는 알고리즘

DFS

DFS와 BFS는 분명히 차이가 있다! (DFS=좁고 깊게, BFS=넓고 얕게)
[프로그래머스 미로탈출] 사전순으로 가장 빠른 경로로 탈출해야 하는 경우, DFS를 이용해야 한다

  • 컴포넌트(요소)란, 무향 그래프가 간선으로 서로 연결되지 않은 몇 개의 조각으로 쪼개져 있는 경우, 각 연결된 정점들의 부분집합

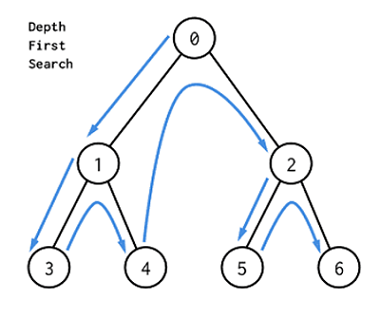
  • 현재 정점과 인접한 간선들을 하나씩 검사하다가, 아직 방문하지 않은 정점으로 향하는 간선이 있다면 그 간선을 무조건 따라감
  • 더 이상 갈 곳이 없는 막힌 정점에 도달하면 포기하고 마지막에 따라왔던 간선을 따라 뒤로 돌아감
import sys
sys.setrecursionlimit(10000)   # RecursionError 방지

adj = [[0] * (n + 1) for _ in range(n+1)]   # 인접행렬
for _ in range(m):
    a, b = map(int, input().split())
    adj[a][b] = 1
    adj[b][a] = 1


visited = [False for _ in range(n+1)]
def dfs(v):
    visited[v] = True

    for i in range(1, n+1):
        if (not visited[i]) and adj[v][i] == 1:
            dfs(i)


# 한 번에 모든 정점을 다 볼 수 없는 경우
# 그래프가 몇 개의 컴포넌트로 나뉘어 있는지 알 수 있음
def dfsAll():
	for i in range(1, n+1):
		if not visited[i]:
			dfs(i)

RecursionError가 발생한다면, 방문 체크를 안해준 게 원인일 것



BFS

가중치가 없는 그래프에서 두 지점 사이의 거리를 찾는 문제는 BFS
가중치가 있다면 플로이드나 다익스트라

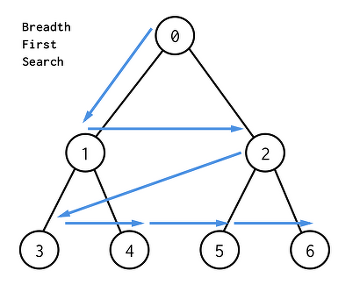
  • 시작점에서 가까운 정점부터 순서대로 방문하는 탐색 알고리즘
  • 시작 지점이 여러 개일 때는 먼저 큐에 저장한 뒤 BFS!
    ​

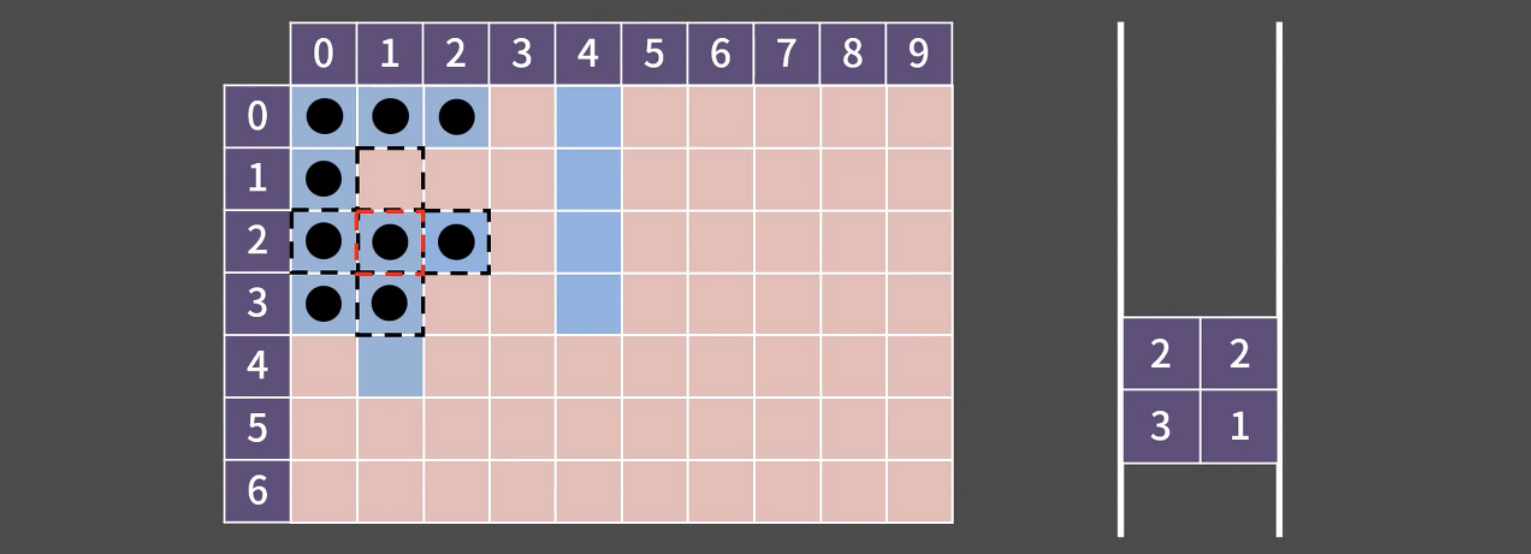
  1. 각 정점을 방문할 때마다 모든 인접 정점들을 검사함
  2. 이 중 처음 보는 정점을 발견하면 이 정점을 방문 예정이라고 기록해 둔 뒤, 큐에 저장
  3. 인접한 정점을 모두 검사하고 나면, 지금까지 저장한 목록에서 다음 정점을 꺼내서 방문하게 됨

​

## BFS의 대표적인 풀이방법 1
adj = [[0] * (n + 1) for _ in range(n+1)]
for i in range(m):
	adj[a][b] = 1
    adj[b][a] = 1
    
visited = [False for _ in range(n+1)]
dist = [0 for _ in range(n+1)]

# v 노드부터 탐색 
def bfs(v):
	q = deque()
    q.append(v)   # v를 방문함 
    visited[v] = True
    
    while q:
    	here = q.popleft()
        
        for i in range(1, n+1):
        	if not visited[i] and adj[here][i] == 1:
            	q.append(i)   # 처음 보는 정점이면 방문 목록에 집어넣음
                visited[i] = True
                dist[i] = dist[here] + 1   # 탐색 레벨 구하기

​

## BFS의 대표적인 풀이방법 2
# 3차원 배열의 경우 -> dx, dy, dx = [0, 0, -1, 1, 0, 0], [-1, 1, 0, 0, 0, 0], [0, 0, 0, 0, -1, 1]
from collections import deque

dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
visited = [[0] * m for _ in range(n)]

def bfs(y, x):
	q = deque()
    q.append([y, x])
    visited[y][x] = 1
    
    while q:
    	y, x = q.popleft()
        
        if y == (n - 1) and x == (m - 1):
        	break
        
        for i in range(4):
        	nx = x + dx[i]
            ny = y + dy[i]
            
            if 0 <= nx < m and 0 <= ny < n and maze[ny][nx] == 1 and visited[ny][nx] == 0:
            	maze[ny][nx] = maze[y][x] + 1   # 최단거리 구하기 
                visited[ny][nx] = 1
                q.append([ny, nx])



서로소 집합

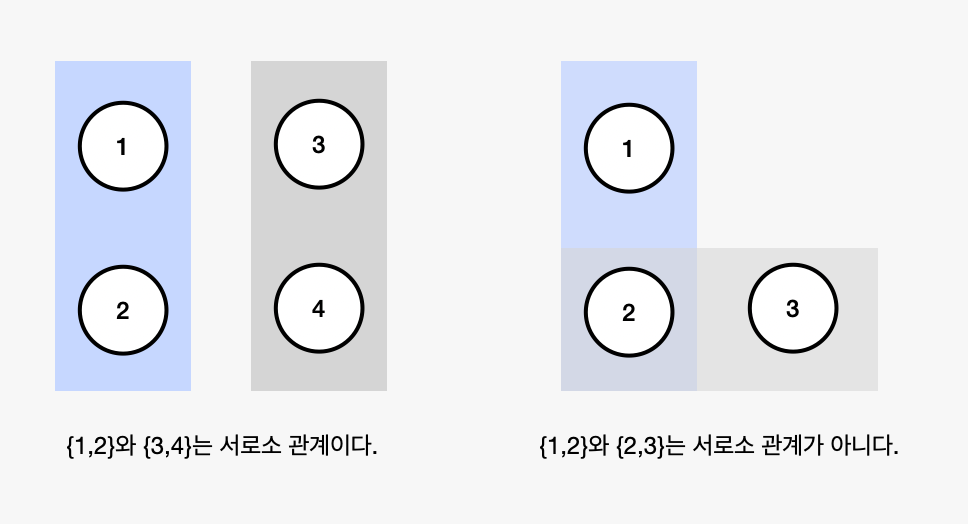
공통 원소가 없는 두 집합​
무방향 그래프 내에서 사이클을 판별할 때 사용할 수 있음 (방향 그래프는 DFS 사용)

서로소 집합 자료구조는 union과 find 2개의 연산으로 조작할 수 있음

  • union(합치기) = 2개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
  • find(찾기) = 특정한 원소가 속한 집합이 어떤 집합인지 알려주는 연산

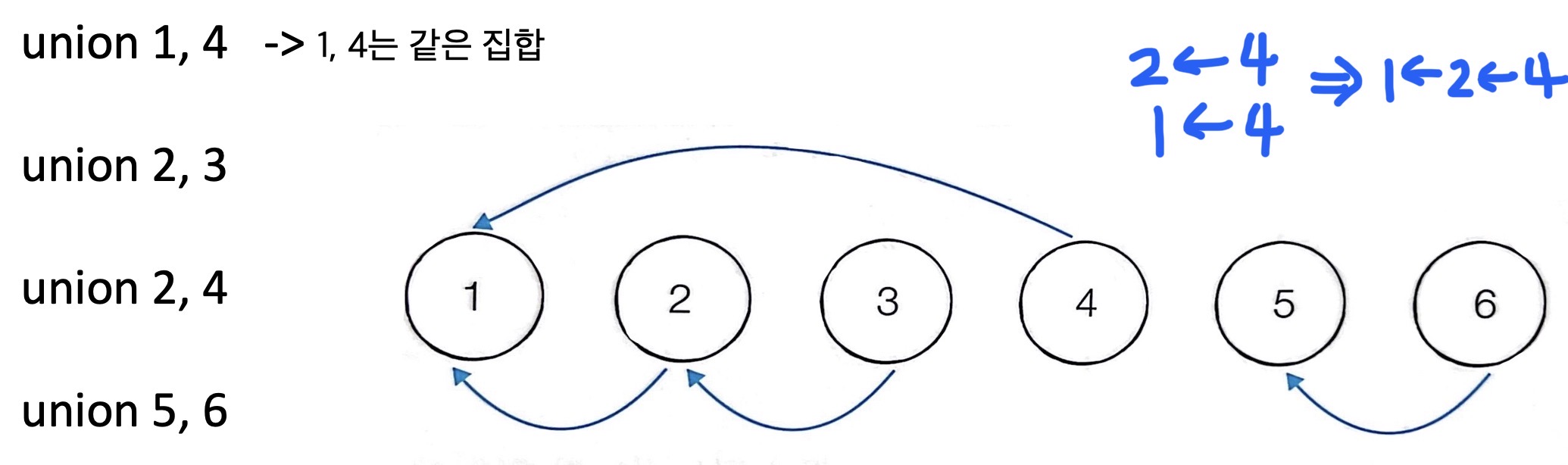
  1. union 연산을 수행하며, 서로 연결된 두 노드 A, B를 확인한다
    • A와 B의 루트 노드 A', B'를 각각 찾는다
    • A'를 B'의 부모 노드로 설정한다(B'가 A'를 가리키도록 한다) -> A, B 그룹은 한 집합으로 묶어진다
  1. 모든 union 연산을 처리할 때까지 1번 과정을 반복한다

​

💡 기본적인 서로소 집합 알고리즘 코드

# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
	# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
    if parent[x] != x:
    	return find_parent(parent, parent[x])
    return parent[x]
    
    
# 두 원소가 속한 집합을 합치기 
def union_parent(parent, a, b):
	a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b:
    	parent[b] = a    # parent[2] = 1
    else:
    	parent[a] = b


# 노드의 개수와 간선의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v + 1)   # 부모 테이블 초기화

# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1):
	parent[i] = i

# union 연산을 각각 수행 
for i in range(e):
	a, b = map(int, input().split())
    union_parent(parent, a, b)
    
# 각 원소가 속한 집합 출력 
for i in range(1, v+1):
	print(find_parent(parent, i), end=' ')   # 1 1 1 1 5 5

​

💡 서로소 집합을 활용한 사이클 판별 코드

def find_parent(parent, x):
	if parent[x] != x:
    	parent[x] = find_parent(parent, parent[x])
    return parent[x]


def union_parent(parent, a, b):
	a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b:
    	parent[b] = a
    else:
    	parent[a] = b


v, e = map(int, input().split())
parent = [0] * (v + 1)

for i in range(1, v+1):
	parent[i] = i


cycle = False

for i in range(e):
	a, b = map(int, input().split())
    if find_parent(parent, a) == find_parent(parent, b):
    	cycle = True
        break
    else:
    	union_parent(parent, a, b)


if cycle:
	print('사이클이 발생했습니다')
else:
	print('사이클이 발생하지 않았습니다')



2️⃣ 문제풀이

백준 벽 부수고 이동하기 2 (🥇3)

# 벽을 K개까지 부수고 이동해도 됨 
q.append([0, 0, 0])
visited = [[[0] * (k + 1) for _ in range(m)] for _ in range(n)]

# (ny, nx)가 벽이 아닐 때 
if visited[ny][nx][z] == 0 and maps[ny][nx] == 0:
	q.append([ny, nx, z])
    visited[ny][nx][z] = visited[y][x][z] + 1

# (ny, nx)는 벽이지만 아직 벽을 부술 기회가 남아 있을 때 
if z < k and maps[ny][nx] == 1 and visited[ny][nx][z+1] == 0:
	q.append([ny, nx, z+1])
    visited[ny][nx][z+1] = visited[y][x][z] + 1



프로그래머스 리코쳇 로봇 (Level 2)

벽/장애물에 부딪칠 때까지 한 방향으로 이동할 때

q = deque()
q.append([sy, sx])
dict = [[-1] * m for _ in range(n)]
dict[sy][sx] = 0
    
while q:
	y, x = q.popleft()
        
    if y == ey and x == ex:
    	answer = dict[y][x]
        break
        
    for i in range(4):
    	ny, nx = y, x
            
        while True:
        	ny += dy[i]
            nx += dx[i]
                
            if ny < 0 or ny >= n or nx < 0 or nx >= m:
            	ny -= dy[i]
                nx -= dx[i]
                break
                
            if board[ny][nx] == 'D':
            	ny -= dy[i]
                nx -= dx[i]
                break
        
        # dist 배열을 사용하지 않으면, 방문한 곳의 위치를 계속 큐에 넣게 됨 -> 무한루프
		if dict[ny][nx] == -1:
        	q.append([ny, nx])
            dict[ny][nx] = dict[y][x] + 1
profile
mingsso
🐥👩‍💻💰
이전 포스트

동적계획법(DP)

다음 포스트

우선순위 큐

0개의 댓글