1️⃣ 수
소수(小數)
1. 반올림
round(소수, 자리수 n) = n+1 자리에서 반올림하여 n째 자리까지 값을 나타냄
"{:.3f}".format(소수)
"{:.3f}".format(1.1700000000000002) = 1.170
round(1.1700000000000002, 3) = 1.17
2. 올림 = math.ceil(소수)
소수(素數)
1과 자기 자신으로만 나누어지는 수 = 약수가 2개인 수
0과 1은 소수도 합성수도 아님
def isPrime(n):
if n < 2:
return False
for i in range(2, int(n**0.5)+1):
if n % i == 0:
return False
return True
에라토스테네스의 체

- 2의 배수인 다른 수를 다 False로 만듦, 3의 배수인 다른 수를 다 False로 만듦
- 4는 이미 소수가 아니라고 표시(False)가 되어있기 때문에 넘어감
메모리 제한이 충분할 때 사용하기
arr = [True for _ in range(n+1)]
for i in range(2, int(n**0.5)+1):
if arr[i]:
for j in range(i+i, n+1, i):
arr[j] = False
소인수분해
정수를 소수의 곱으로 나타내는 것, 모든 자연수는 소인수분해하는 방법이 한 가지만 존재함

1) N이 i로 나눠지는지 확인하고, 나눠진다면 i를 소인수 목록에 추가하고 N으로 나눔
2) N이 i로 나눠지지 않을 때까지 이 작업을 계속 반복함
3) N이 더이상 i로 나눠지지 않으면 i를 1 증가시킴 -> N이 1이 되는 순간 작업이 끝남
-> 이때 수학적으로 i는 반드시 소수가 됨
최대공약수(GCD)와 최소공배수(LCM)
최대공약수 = math.gcd(숫자들)
A x B = GCD(A, B) x LCM(A, B)
+) 유클리드 호제법
두 수 A, B에 대해 A를 B로 나눈 나머지를 r이라고 하면 GCD(A, B) = GCD(B, r)
진법
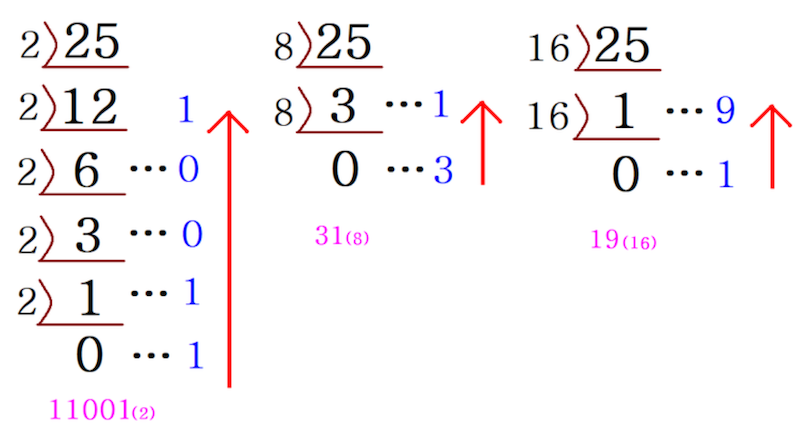
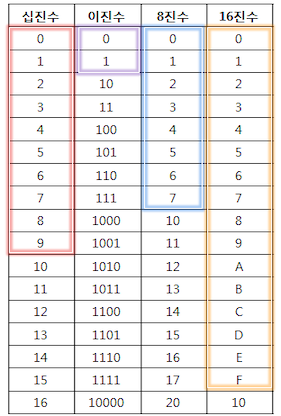
n진수 -> 10진수
int(string, 진법)
print(int('111', 2)) #7
print(int('333', 4)) #63
print(int('FFF', 16)) #4095
10진수 -> 2,8,16진수
2, 8, 16진수는 bin(), oct(), hex() 함수를 지원
(앞의 진법 표시를 지우려련 [2:]를 하면 됨)
print(bin(10)) #0b1010
print(oct(10)) #0o12
print(hex(10)) #0xa
10진수 -> n진수
def convert(num, base):
temp = "0123456789ABCDEF"
q, r = divmod(num, base) # 몫과 나머지를 리턴하는 함수 divmod
if q == 0:
return temp[r]
else:
return convert(q, base) + temp[r] # 재귀 비트 연산자
- a & b (AND)
- a | b (OR)
- a ^ b (XOR)
- ~a (NOT)
13 ^ 9 # 4 (비트 XOR)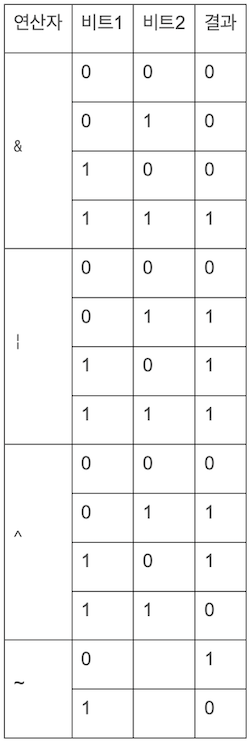
행렬의 곱셈
# 행렬 A x 행렬 B
answer = [[0] * len(B[0]) for _ in range(len(A))]
for i in range(len(A)):
for j in range(len(B[0])):
temp = 0
for k in range(len(A[0])):
temp += A[i][k] * B[k][j]
answer[i][j] = temp관련 함수
abs() = 절댓값 함수
2️⃣ 순열과 조합
순열
- 구현
def permutation(arr, r):
arr.sort()
used = [0 for _ in range(len(arr))]
def generate(chosen, used):
if len(chosen) == r: # r개를 다 골랐으면
print(chosen)
return
for i in range(len(arr)):
if not used[i]: # 아직 고르지 않은 수라면
chosen.append(arr[i])
used[i] = 1
generate(chosen, used)
used[i] = 0
chosen.pop()
generate([], used)
- 사용법
from itertools import permutations
data = itertools.permutation(arr, 2)from itertools import product
# 2개를 뽑아 일렬로 나열하는 경우의 수(단, 중복 허용)
data = itertools.product(arr, repeat=2)
프로그래머스 줄 서는 방법
사람을 나열하는 방법(n!)을 사전 순으로 나열했을 때, k번째 방법 리턴
def solution(n, k):
answer = [i for i in range(1, n+1)]
stack = []
k = k - 1
while answer:
idx = k // math.factorial(n-1)
stack.append(answer[idx])
del answer[idx]
k = k % math.factorial(n-1)
n -= 1[1,2,3,4]가 이루는 모든 경우의 수에서 7번째 방법을 구하려고 할 때,
가장 앞자리가 1이 되는 경우는 1~6번 -> 1을 제외한 2,3,4 3개의 숫자가 정렬 = 3!
중복순열
중복 가능한 n개에서 순서를 고려하며 r개를 택하는 경우의 수
from itertools import product
print(product(arr, repeat=r)) 조합
서로 다른 n개 중에서 r개(n≥r) 취하여 조를 만들 때, 만들 수 있는 조의 개수
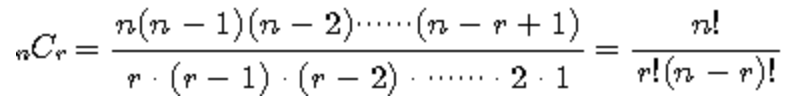
from itertools import combinations
print(list(combinations([1, 2, 3, 4], 2))
# 결과 = [(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)] (오름차순으로 뽑음!!)- 인자로 set 가능
프로그래머스 시소 짝꿍 (Level 2)
https://school.programmers.co.kr/learn/courses/30/lessons/152996
for k, v in kind.items():
# 본인과 같은 무게의 친구가 있을 경우 -> 한 팀에서 두 명을 고르는 거라 조합
if v > 1:
answer += (v * (v - 1)) // 2
# 본인의 몸무게로 평형을 맞출 수 있는 경우
for i, j in pos:
# 180 * 4 = 360 * 2 => (180 * 4) / 2 = 360
temp = k * i / j
if temp in kind:
answer += v * kind[temp] # 각 팀에서 한 명씩 고르는 거라 곱해줌
kind[k] = 0 # 중복 처리 방지 중복조합
중복 가능한 n개에서 순서를 생각하지 않고 r개를 택하는 경우의 수
from itertools import combinations_with_replacement3️⃣ 집합 set
교집합 = A & B
합집합 = A | B
set 안에는 리스트가 들어갈 수 없음! 튜플로 바꿔줘야 함
s1.discard(2) -> 값이 없어도 에러가 발생하지 않음
s1.remove(2) -> 값이 없으면 에러
s1.issubset(s2) -> s1 ⊂ s2이면 True (s1, s2는 모두 집합)
문제풀이
프로그래머스 방문 길이 (Level 2)
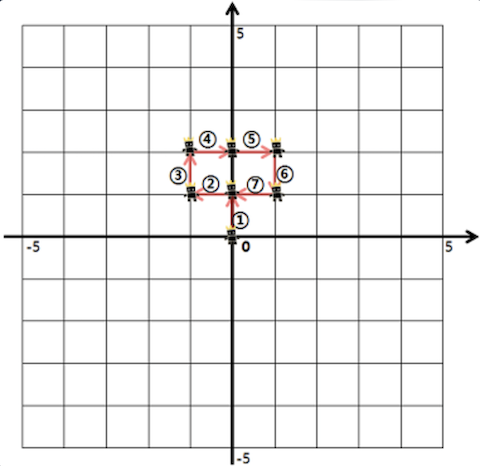
처음 방문한 선의 개수 구하기 -> 선의 시작점과 끝점 집합에 넣기
4️⃣ 직선의 방정식
두 직선의 교점 구하기
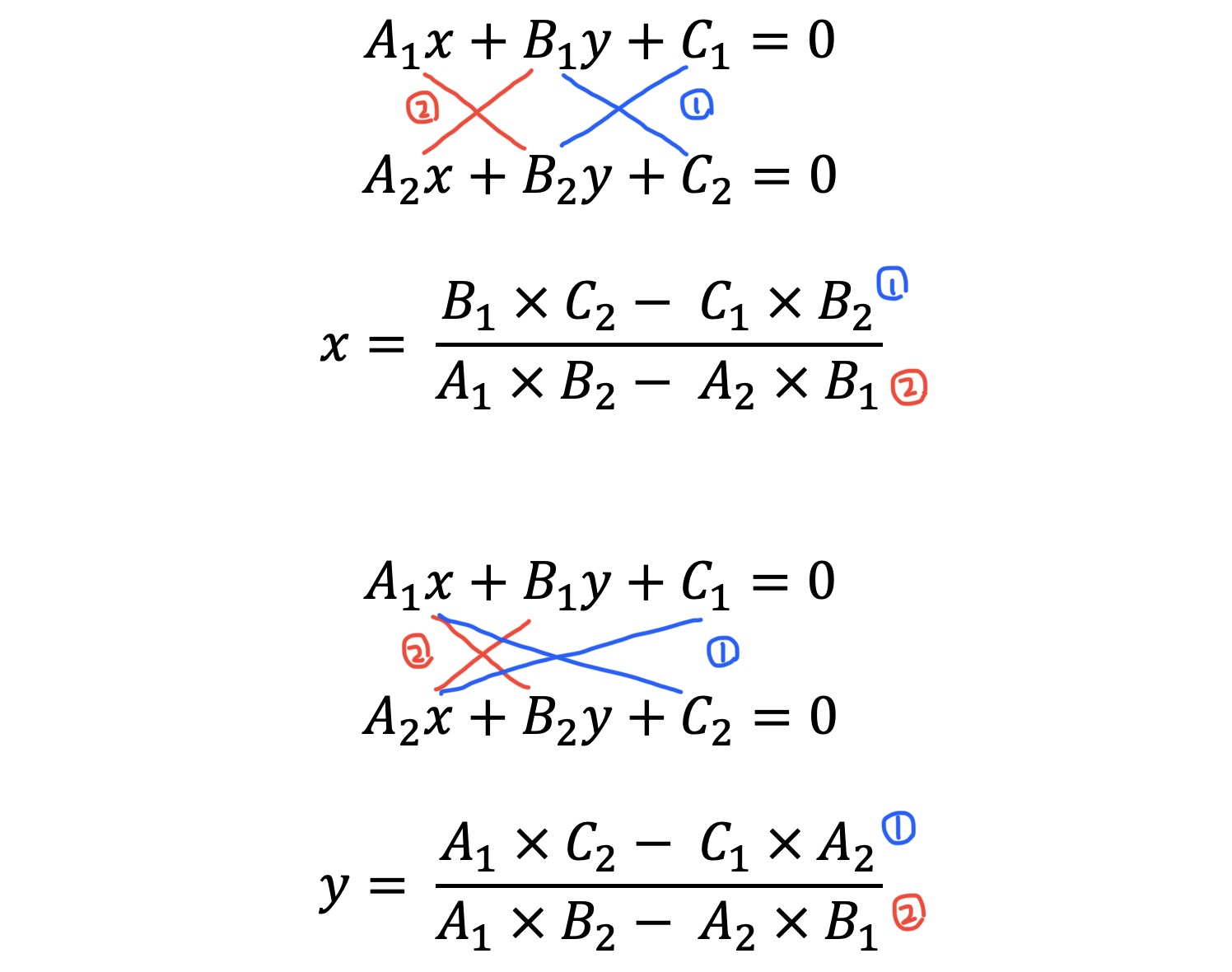
# A1x+B1y+C1=0과 A2x+B2y+C2=0
def count(line1, line2):
a1, b1, c1 = line1
a2, b2, c2 = line2
if a1 * b2 == b1 * a2:
return None
x = (b1 * c2 - c1 * b2) / (a1 * b2 - b1 * a2)
y = (c1 * a2 - a1 * c2) / (a1 * b2 - b1 * a2)
if x == int(x) and y == int(y):
return [int(x), int(y)]문제풀이
프로그래머스 점 찍기 (Level 2)
https://school.programmers.co.kr/learn/courses/30/lessons/140107
원점(0, 0)으로부터 x축 방향으로 a*k(a = 0, 1, 2, 3 ...), y축 방향으로 b*k(b = 0, 1, 2, 3 ...)만큼 떨어진 위치에 점을 찍을 때, 원점과 거리가 d를 넘는 위치에는 점을 찍지 않음
찍을 수 있는 점의 개수는?
# bk = (r^2 - (ak)^2)^0.5
# y = (r^2 - x^2)^0.5
for x in range(0, d+1, k):
res = int((d**2 - x**2)**0.5)
answer += (res // k) + 1