우선순위 큐

1️⃣ 개념 및 구현

• 가장 먼저 입력된 자료가 먼저 꺼내지는 게 아니라, 우선순위가 높은 자료가 가장 먼저 꺼내짐

• 시간복잡도
  • 원소의 추가 = O(lgN)
  • 우선순위가 가장 높은 원소의 확인 = O(1)
  • 우선순위가 가장 높은 원소의 제거 = O(lgN)

• 힙을 이용해 간단히 구현할 수 있음(힙은 가장 큰 원소를 찾는데 최적화된 형태의 이진 트리이기 때문)
  • 이진 검색 트리와 힙은 이진 트리라는 공통점만 있을 뿐, 다른 자료구조임!

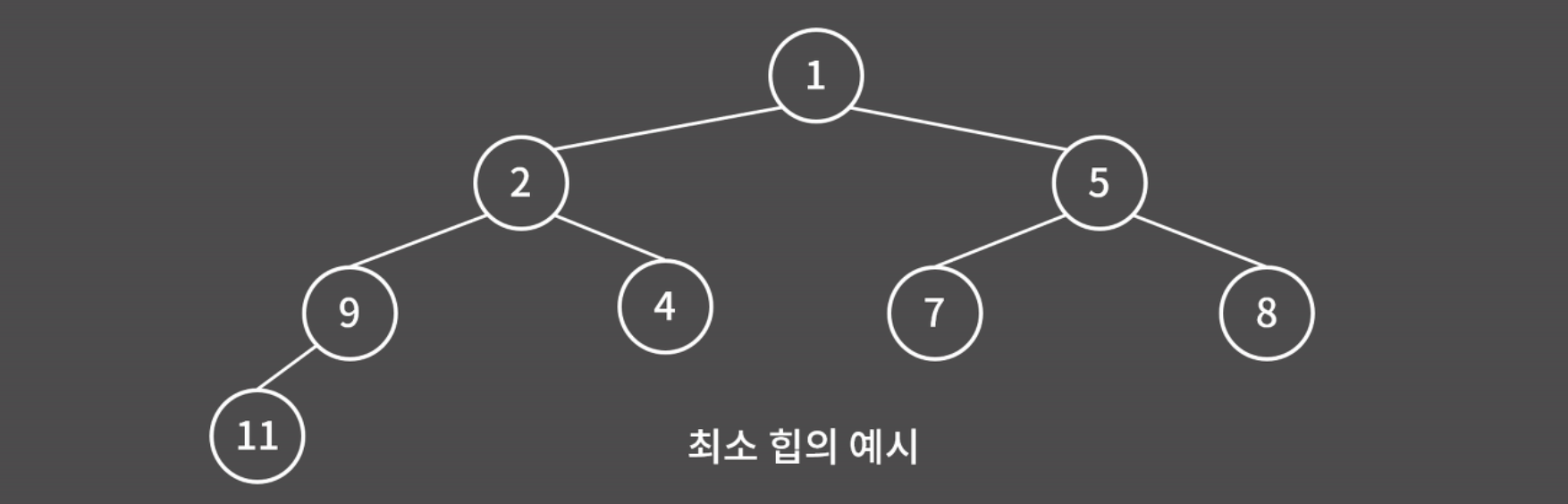
최소 힙에선 부모가 자식보다 작아야 하고(루트=최소값), 최대 힙에선 부모가 자식보다 커야 함(루트=최댓값)
​

원소 삽입 순서

• 높이가 낮은 곳부터, 높이가 같은 정점의 경우에는 왼쪽부터 채워나감
• 이진 검색 트리와는 다르게, 힙은 불균형이 발생하지 않고 늘 균형이 잘 맞는 이진 트리가 됨
• 트리에 포함된 노드의 개수만으로 트리의 모양이 정해짐

​

배열을 이용한 힙의 구현

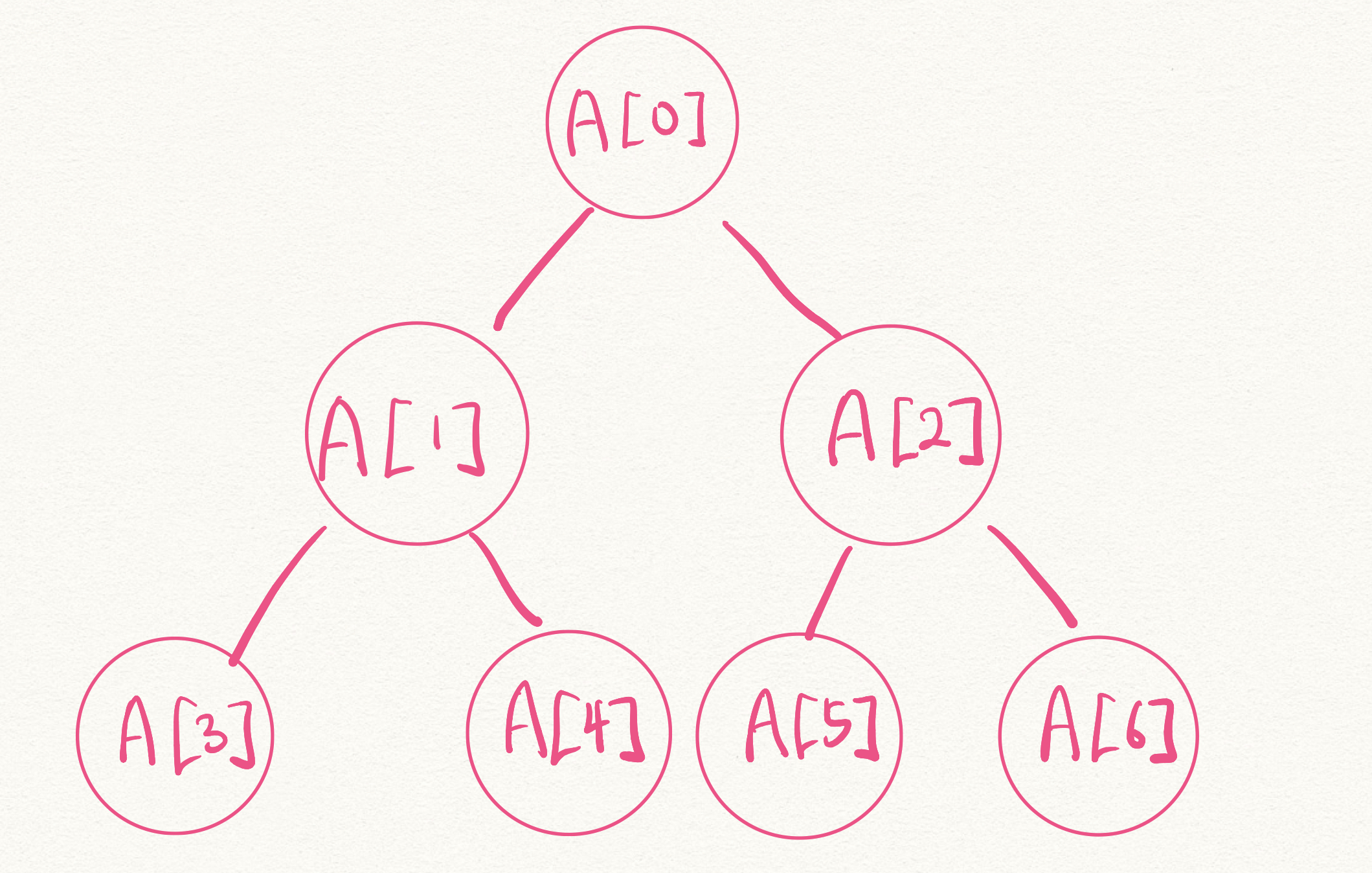
• A[i]에 대응되는 노드의 왼쪽 자손은 A[2*i+1]에 대응됨
• A[i]에 대응되는 노드의 오른쪽 자손은 A[2*i+2]에 대응됨
• A[i]에 대응되는 노드의 부모는 A[(i-1)/2]에 대응됨 (나눗셈 결과는 내림)

​

새 원소의 삽입 -> O(lgN)

• sort 함수의 시간복잡도는 O(NlgN) -> 우선순위 큐가 시간복잡도가 더 적음!
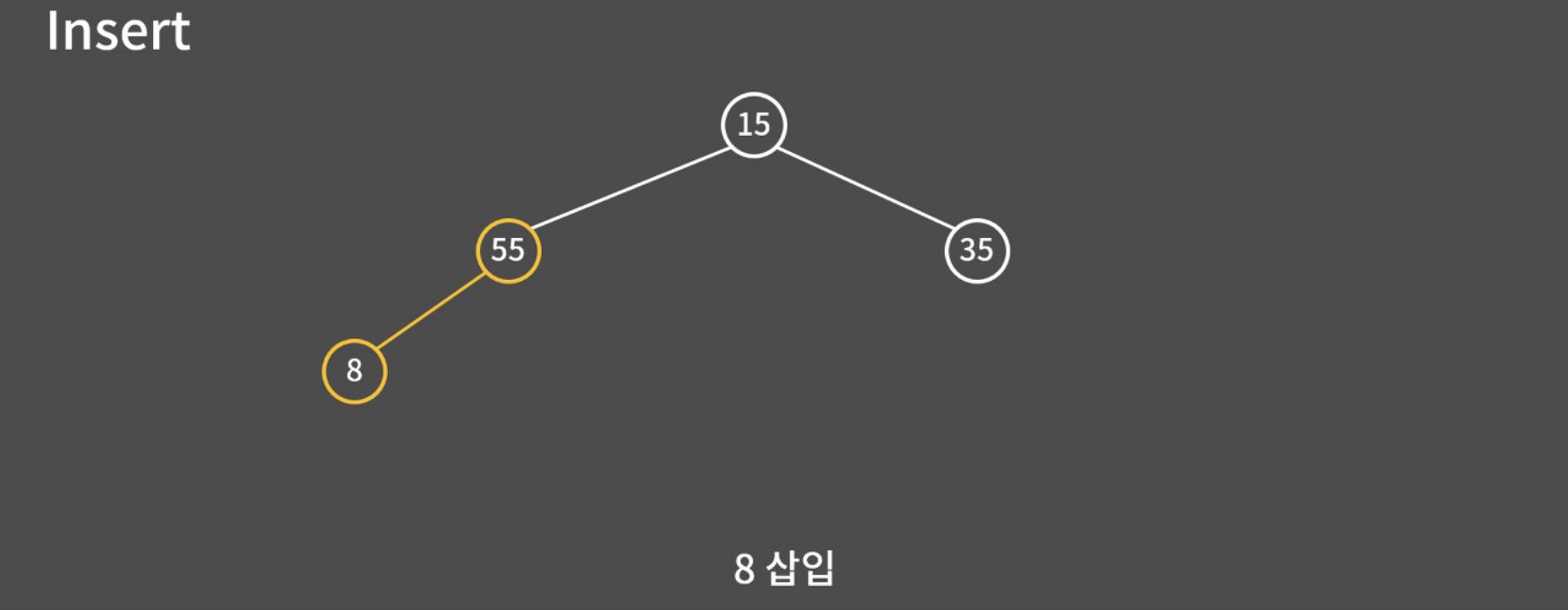
• 모양 규칙에 의해 새 노드는 항상 힙의 맨 끝에 추가됨
• 마지막에 추가한 새 원소를 자신의 부모 노드가 가진 원소와 비교하고, 부모 노드가 가진 원소가 작다면 두 원소의 위치를 바꿈
• 새 원소가 더 크거나 같은 원소를 가진 부모 노드를 만나거나, 루트에 도달할 때까지 반복하면 됨

2️⃣ 파이썬 heap 라이브러리

항상 정렬된 상태로 추가되고 삭제됨 -> 첫번째 원소가 최소값

# 파이썬은 최대힙은 제공하지 않음 -> 원소의 부호를 바꿔서 최대힙 구현
import heapq

# 원소 추가하기
heapq.heappush(minHeap, newValue)
heapq.heappush(minHeap, [arr[i][1], arr[i][0]])

# 원소 삭제하기
heapq.heappop(minHeap)

3️⃣ 문제 풀이

💡 힙에 같은 값이 입력될 경우 항상 주의

* 백준 보석도둑 (🥇2)

https://www.acmicpc.net/problem/1202

상덕이가 털 보석점에는 보석이 총 N개 있다. 각 보석은 무게 M와 가격 V를 가지고 있다. 상덕이는 가방을 K개 가지고 있고, 각 가방에 담을 수 있는 최대 무게는 C이다. 각 가방에는 한 개의 보석만 넣을 수 있다.
상덕이가 훔칠 수 있는 보석의 최대가격은?
​

for _ in range(n):
    a, b = map(int, input().split())
    heapq.heappush(jewel, [a, -b])   # [무게, -가격] -> 무게 작은 순, 가격 높은 순

bag = []
for _ in range(k):
    bag.append(int(input()))   # 각 가방에 담을 수 있는 최대 무게

bag.sort()   # 가방 무게 가벼운 순 
steal = []
answer = 0

for i in range(k):   # 각 가방 별로 
    while jewel:
        temp = heapq.heappop(jewel)
        if bag[i] >= temp[0]:   # 이 가방에 보석을 담을 수 있으면 
            heapq.heappush(steal, temp[1])   # 가격만 힙에 담아줌 -> temp[1]은 음수라 그대로 넣어줌(최대힙이 됨!)
        else:   # 담을 수 없으면 다시 넣어줌 
            heapq.heappush(jewel, temp)
            break

    if len(steal) != 0:
        answer += -heapq.heappop(steal)   # 넣을 수 있는 보석 중 가장 비싼 것을 넣어줌 

* 프로그래머스 디펜스 게임 (Level 2)

https://school.programmers.co.kr/learn/courses/30/lessons/142085

준호가 보유한 병사 n명 중 enemy[i]명을 소모하여 enemy[i]마리의 적을 막을 수 있다. 무적권은 최대 k번 사용할 수 있으며 병사의 소모 없이 한 라운드의 공격을 막을 수 있다.
준호는 최대 몇 라운드까지 막을 수 있을까?
​

for i in range(len(enemy)):
	total += enemy[i]   # i라운드까지 총 적의 수 
	if total <= n:
		heapq.heappush(maxHeap, -enemy[i])
		answer += 1
	elif k > 0:   # 적의 수가 병사의 수보다 많을 경우
		k -= 1
		heapq.heappush(maxHeap, -enemy[i])
		total += heapq.heappop(maxHeap)
		answer += 1
	else:
		break

각 라운드의 적의 수와 n을 비교하는 게 아니라, i 라운드까지 총 적의 수와 비교함

* 백준 강의실 (🥇5)

https://www.acmicpc.net/problem/1374

N개 강의의 시작하는 시간과 끝나는 시간을 알고 있을 때, 필요한 최소 강의실의 수?
​

# arr = [강의번호, 시작시간, 종료시간]
arr.sort(key=lambda x:x[1])   # 시작 시간으로 오름차순 정렬

heap = []
answer = 0

for i in arr:
    while heap and heap[0] <= i[1]:   # 가장 일찍 끝나는 시간보다 시작시간이 크면 
        heapq.heappop(heap)   # 이 회의는 i번째 회의랑 동시에 진행할 수 있음 

    heapq.heappush(heap, i[2])   # i번째 회의의 끝나는 시간을 추가
    answer = max(answer, len(heap))  

중간에 강의실이 10개 필요하면 답은 10인거임

* 프로그래머스 디스크 컨트롤러 (Level 3)

https://school.programmers.co.kr/learn/courses/30/lessons/42627

각 작업에 대해 [작업이 요청되는 시점, 작업의 소요시간]을 담은 2차원 배열 jobs가 매개변수로 주어질 때, 작업의 요청부터 종료까지 걸린 시간의 평균을 가장 줄이는 방법으로 처리하면 평균이 얼마나 되는지 리턴
​

def solution(jobs):
	answer, now, i = 0, 0, 0   # now는 현재 시점
    start = -1   # 바로 이전에 완료한 작업의 시작 시간
    minHeap = []
    
    while i < len(jobs):
    	for j in jobs:
        	# 현재 시점에서 처리할 수 있는 작업이라면
            # 바로 이전에 완료한 작업의 시작 시간 < 작업 요청시점 <= 현재 시점
            # jobs 전체를 순회하기 때문에, start가 없다면 예전에 완료한 작업도 추가될 것
            if start < j[0] <= now:
            	heapq.heappush(minHeap, [j[1], j[0]])   # 소요시간 짧은 것부터
            
        # 처리할 수 있는 작업이 존재하면
        if len(minHeap) > 0:
        	cur = heapq.heappop(minHeap)
            start = now
            now += cur[0]
            answer += (now - cur[1])
            i += 1
        else:
        	now += 1
    
    return answer // len(jobs)