재귀, 백트래킹, 분할정복

1️⃣ 개념

재귀

하나의 함수에서 자기 자신을 다시 호출해 작업을 수행하는 알고리즘

수학적 귀납법
1. n=1일 때, 즉 P(1)이 성립함을 증명하고
2. n=k일 때, 즉 P(k)가 성립한다고 가정하면 n=k+1일 때, 즉 P(k+1)도 성립함을 증명함

• 올바른 재귀 함수는 반드시 특정 입력에 대해서는 자기 자신을 호출하지 않고 종료되어야 함 (base condition)
• 재귀는 반복문으로 구현했을 때에 비해 코드가 간결하지만 메모리/시간에서는 손해를 봄 -> 재귀가 깊어지면 런타임 에러가 발생할 수 있음

백트래킹

현재 상태에서 가능한 모든 후보군을 따라 들어가며 탐색하는 알고리즘

## 1부터 N까지의 자연수 중에서 중복 없이 M개 고르기 

series = []
visited = [False for _ in range(n+1)]

def pick(cnt):
	if cnt == m:   # M개의 수를 모두 택했으면 
    	for i in series:
        	print(i, end=' ')   # series에 기록해둔 수를 출력 
        print()
    
    else:
    	# k=m이 아니라면 1과 n까지의 수를 차례로 확인하여 아직 쓰이지 않은 수를 찾아냄 
        for i in range(1, n+1):
        	if not visited[i]:   # 아직 i가 사용되지 않았으면 
            	series.append(i)
                visited[i] = True
                pick(cnt+1)
                series.pop()
                visited[i] = False

pick(0)

2️⃣ 문제 풀이

* 하노이탑 이동 순서

1. n-1개의 원판을 기둥1에서 기둥2로 옮긴다
2. n번 원판을 기둥1에서 기둥3으로 옮긴다
3. n-1개의 원판을 기둥2에서 기둥3으로 옮긴다
   -> 원판이 n-1개일 때 옮길 수 있으면 원판이 n개일 때도 옮길 수 있음
   ​

def put(a, b, n):
    if n == 1:
        print(a, b)
        return
    
    put(a, 6-a-b, n-1)   # n-1개의 원판을 기둥1에서 기둥2로 옮김 
    print(a, b)   # n번 원판을 기둥1에서 기둥3으로 옮김 
    put(6-a-b, b, n-1)   # n-1개의 원판을 기둥2에서 기둥3으로 옮김 

put(1, 3, n)

* N-Queen

퀸은 가로, 세로, 대각선으로 이동할 수 있을 때, 체스판 위의 n개의 퀸이 서로를 공격할 수 없도록 배치하는 방법의 수?
​

def adjacent(x):
	for i in range(x):   # x까지 
    	# 열이 같거나 대각선이 같으면 False
        if row[x] == row[i] or abs(row[x] - row[i]) == x - i:
        	return False
    
    return True


def dfs(x):
	global answer
    
    if x == n:   # n개의 퀸을 다 놓아야 한 가지 방법이 됨 
    	answer += 1
    else:
    	# 각 행에 퀸 놓기 
        for i in range(n):
        	if visited[i]:
            	continue
                
        	row[x] = i
            if adjacent(x):   # 행,열,대각선 체크 함수 -> True이면 계속 진행 
            	visited[i] = True
            	dfs(x + 1)
                visited[i] = False

* 부분수열의 합

합이 s가 되는 부분수열의 개수 구하기

def pick(cnt, tot):
	global answer
    
    if cnt == n:
    	if tot == s:
        	answer += 1
    else:
    	# arr[cnt]를 더한 경우와 더하지 않은 경우 
        pick(cnt+1, tot)
        pick(cnt+1, tot+arr[cnt])

* 프로그래머스 쿼드 압축 후 개수 세기 (Level 2)

https://school.programmers.co.kr/learn/courses/30/lessons/68936

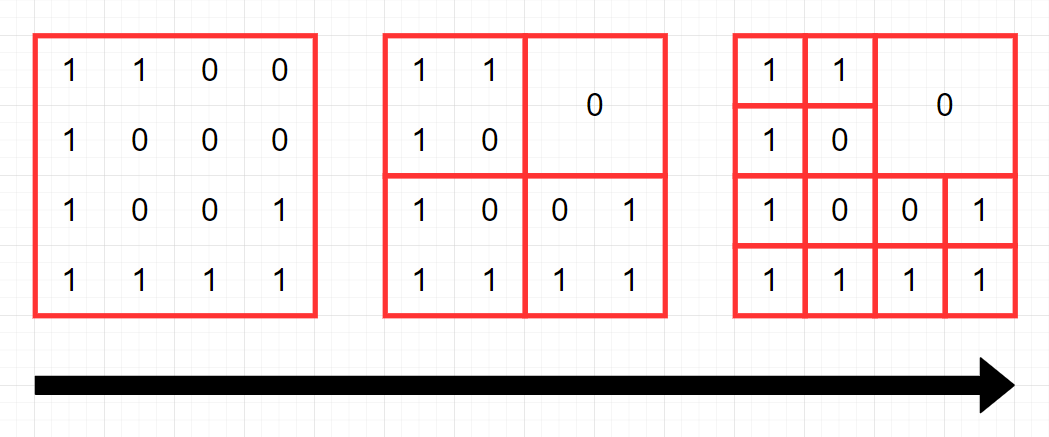
def solution(arr):
	answer = [0, 0]   # 압축 결과 [0의 개수, 1의 개수]
    n = len(arr)
    
    def compress(y, x, n):
    	start = arr[y][x]
        
        for i in range(y, y+n):
        	for j in range(x, x+n):
            	if arr[i][j] != start:
                	n //= 2
                    compress(y, x, n)
                    compress(y, x+n, n)
                    compress(y+n, x, n)
                    compress(y+n, x+n, n)
                    return 
        
        answer[start] += 1
    
    compress(0, 0, n)
    return answer