정렬, 입출력

1️⃣ 개념

삽입 정렬 (Insertion Sort)

정렬 범위를 한 칸씩 확장하면서 새롭게 정렬 범위에 들어온 값들을 기존 값들과 비교하여 알맞은 자리에 삽입하는 방법

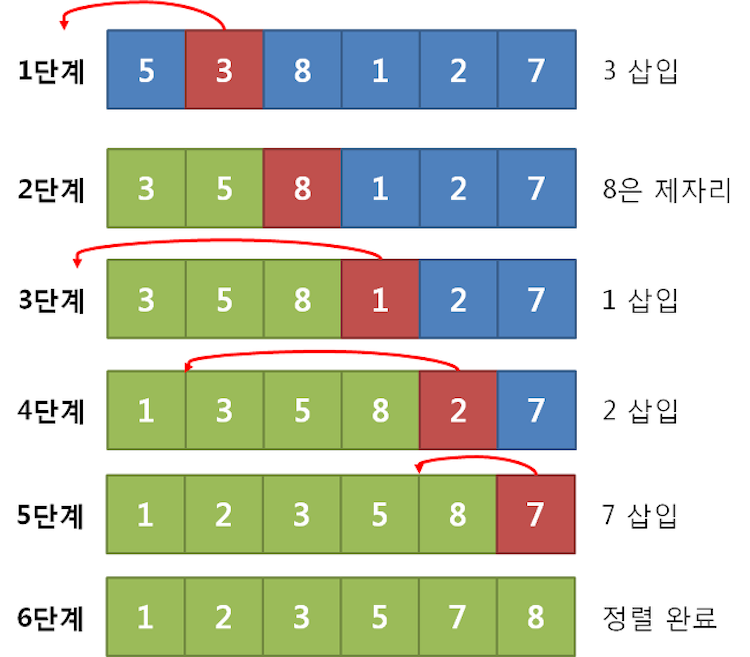
시간복잡도는 최선의 경우 O(n), 평균/최악의 경우 O(n^2)

1. 배열의 i번째(시작은 0) 값을 선택한다
2. 선택한 원소의 왼쪽(이미 정렬된 부분)으로 끝까지 차례대로 돌면서 더 큰 값이 나오면 교환한다
3. 배열의 마지막까지 i를 1씩 증가시키며 1~2를 반복한다
   ​

def insertion_sort(arr):
    for end in range(1, len(arr)):
        for i in range(end, 0, -1):
            if arr[i-1] > arr[i]:
                arr[i-1], arr[i] = arr[i], arr[i-1]

선택 정렬 (Selection Sort)

배열에서 위치를 선택하고, 그 위치에 들어갈 값을 찾아 교환하는 방법

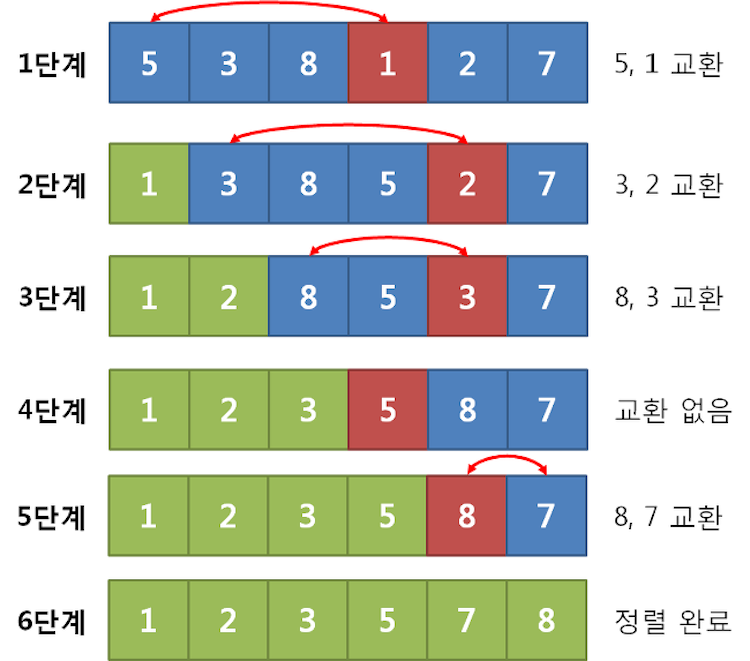
시간복잡도는 최선/평균/최악의 경우 O(n^2)

1. 배열의 i번째(시작은 0) 값을 선택한다
2. 선택한 위치의 값을 최소값으로 둔다
3. 바로 다음(i+1)부터 배열의 마지막까지 차례대로 돌면서 최소값을 갱신한다
4. i번째 값과 최소값을 교환한다(위치를 바꾼다)
5. i가 (배열의 크기-1)이 될 때 까지 i를 1 증가시키고 1~4를 반복한다.
   ​

def selection_sort(arr):
	for i in range(len(arr)-1):
    	min_idx = i
        for j in range(i+1, len(arr)):
        	if arr[j] < arr[min_idx]:
            	min_idx = j
        
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

버블 정렬 (Bubble Sort)

배열을 순회하면서 인접한 두 개의 데이터를 비교하고 교환하는 방법

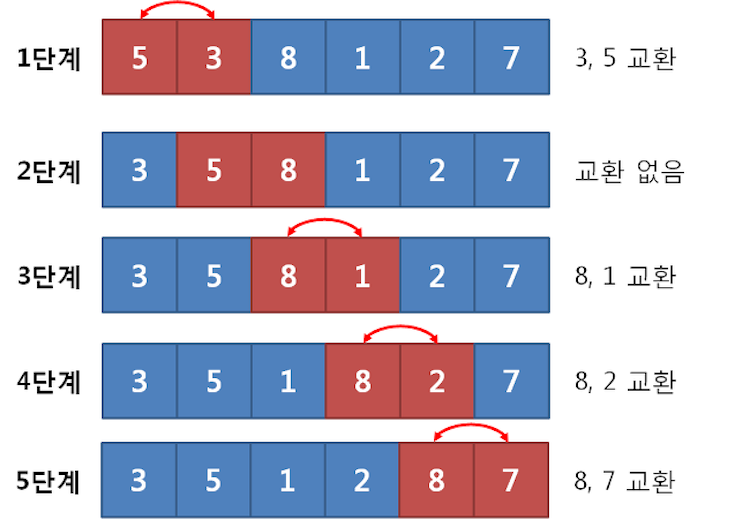
시간복잡도는 최선/평균/최악의 경우 O(n^2)

1. 배열의 j번째(시작은 0) 값과 그 다음 값을 비교하고 순서에 맞게 교환한다.
2. j를 1 증가시키며 i까지 과정 1을 반복한다.
3. 1~2를 반복하되 한 사이클이 끝나면 i를 1 감소시켜 비교 범위를 점점 좁힌다. (가장 큰 값이 제일 뒤로 가기 때문에)

def bubble_sort(arr):
	for i in range(len(arr)-1, 0, -1):
    	for j in range(i):
        	if arr[j] > arr[j+1]:
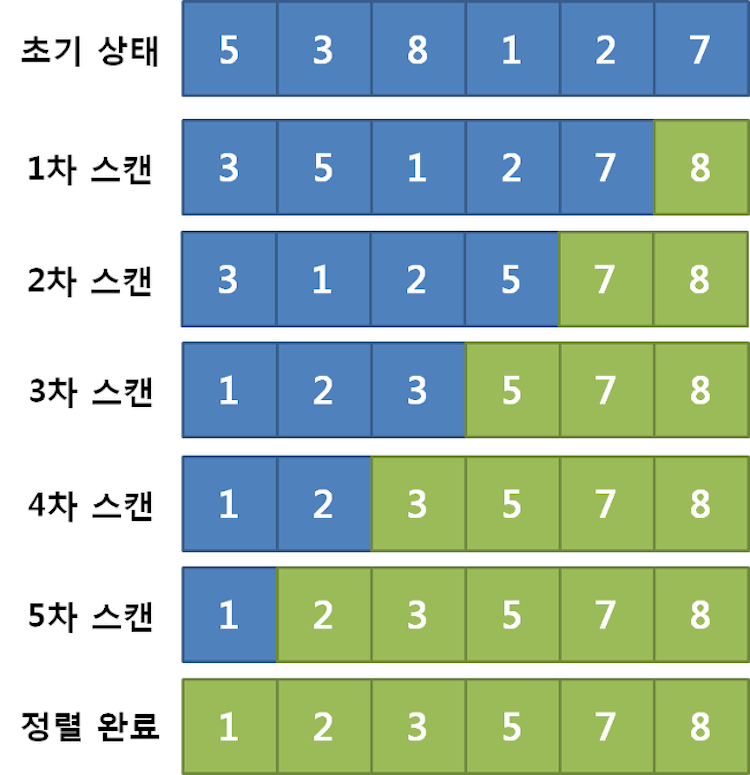
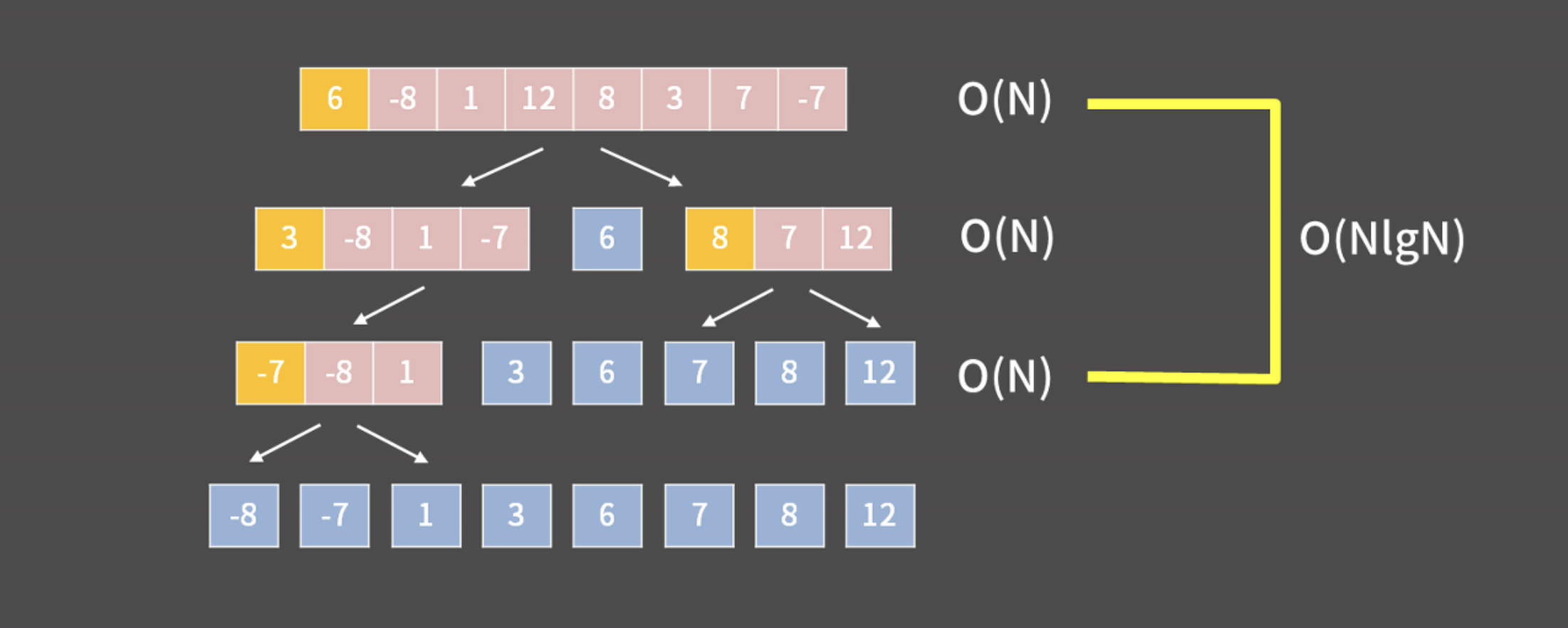
            	arr[j], arr[j+1] = arr[j+1], arr[j]

병합 정렬 (Merge Sort)

재귀적으로 수열을 나눠 정렬한 뒤 합침 -> 주어진 배열을 원소가 하나밖에 남지 않을 때까지 계속 둘로 쪼갠 후에 다시 크기 순으로 정렬

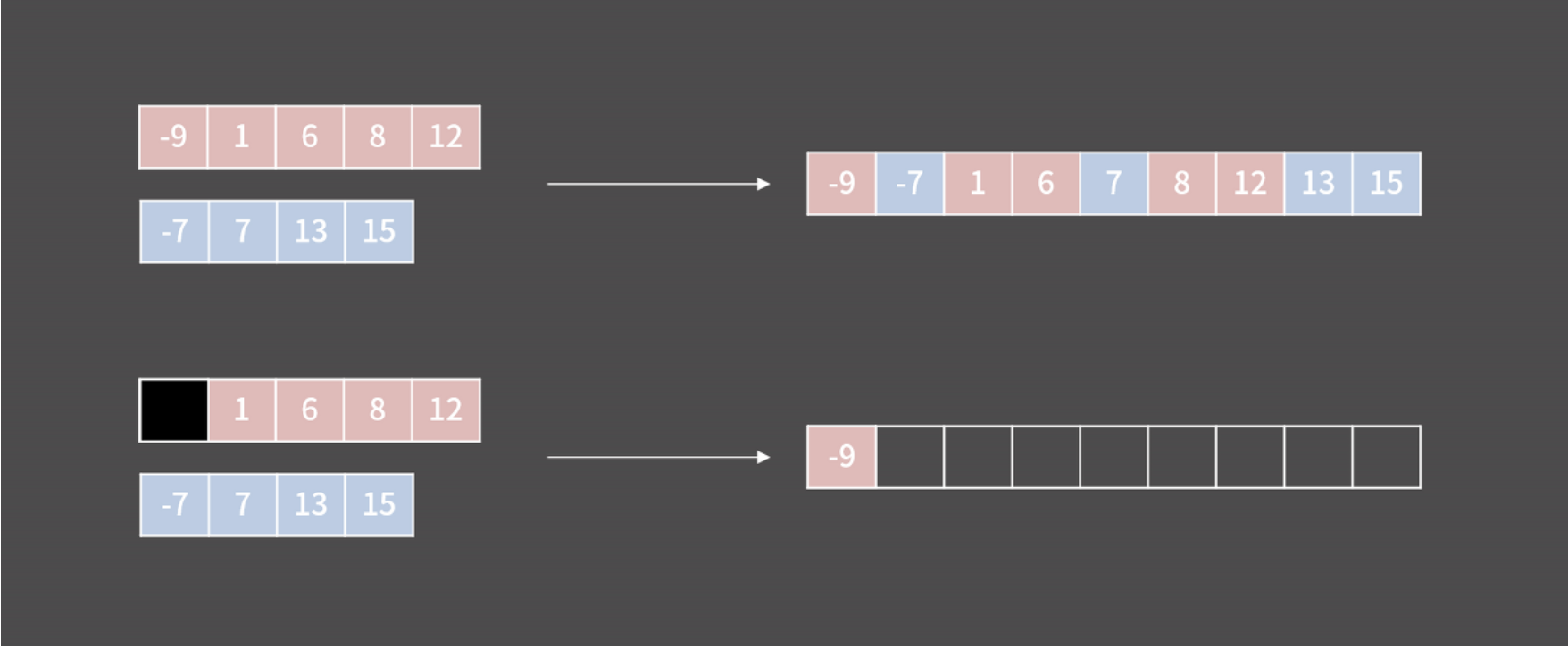
시간복잡도는 최선/평균/최악의 경우 O(nlgn)

def merge_sort(arr):
	if len(arr) < 2:
    	return arr
    
    # 리스트의 길이가 1이 될 때까지 리스트를 둘로 나누기
    mid = len(arr) // 2
    low_arr = merge_sort(arr[:mid])    # 재귀
    high_arr = merge_sort(arr[mid:])    # 재귀 
    
    # 두 리스트를 합쳐서 정렬된 리스트 만들기 
    merged_arr = []
    l, h = 0, 0
    while l < len(low_arr) and h < len(high_arr):
    	if low_arr[l] < high_arr[h]:
        	merged_arr.append(low_arr[l])
            l += 1
        else:
        	merged_arr.append(high_arr[h])
            h += 1
    
    merged_arr += low_arr[l:]
    merged_arr += high_arr[h:]
    
    return merged_arr

Stable Sort

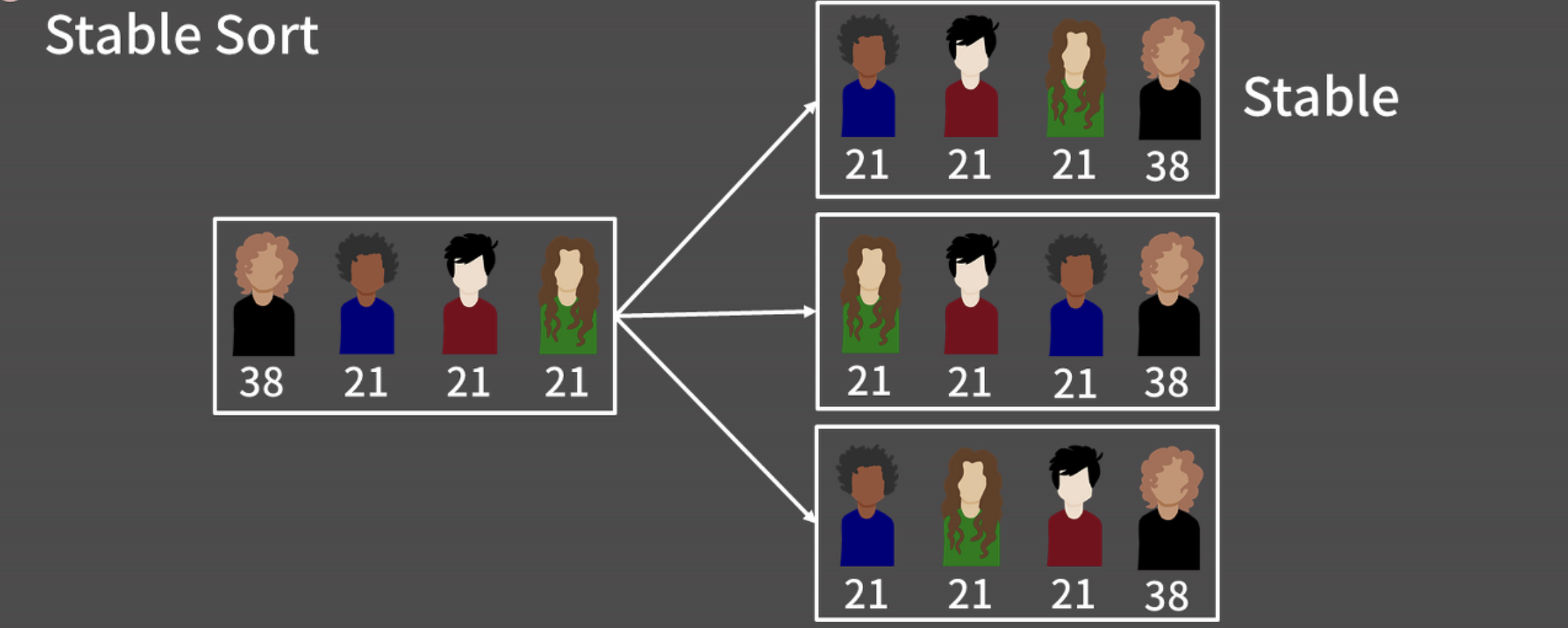
우선순위가 같은 원소가 여러 개일 땐 정렬한 결과가 유일하지 않을 수 있음
-> 우선순위가 같은 원소들끼리는 원래의 순서를 따라가도록 하는 정렬
-> Bubble, Insertion, Merge Sort는 Stable Sort

퀵 정렬 (Quick Sort)

• 퀵 소트는 매 단계마다 피벗이라고 이름 붙은 원소 하나를 제자리로 보내는 작업을 반복함
• 피벗을 제자리로 보내겠다는 건 피벗의 왼쪽은 피벗보다 작은 원소가, 오른쪽에는 피벗보다 큰 원소가 오게끔 하는 것
• 피벗은 맨 왼쪽 원소로 선택함

시간복잡도는 최선/평균의 경우 O(nlgn), 최악의 경우 O(n^2)

• 리스트가 오름차순이나 내림차순일 때 시간복잡도가 O(N^2)가 됨
• sort 함수 등 언어 차원에서 기본 제공하는 내장 정렬 함수 대부분은 퀵 정렬을 기본으로 함

def quick_sort(arr):
	if len(arr) < 2:
    	return arr
    
    pivot = arr[len(arr)//2]
    low_arr, equal_arr, high_arr = [], [], []
    
    for i in range(len(arr)):
    	if arr[i] < pivot:
        	low_arr.append(arr[i])
        elif arr[i] > pivot:
        	high_arr.append(arr[i])
        else:
        	equal_arr.append(arr[i])
    
    return quick_sort(low_arr) + equal_arr + quick_sort(high_arr)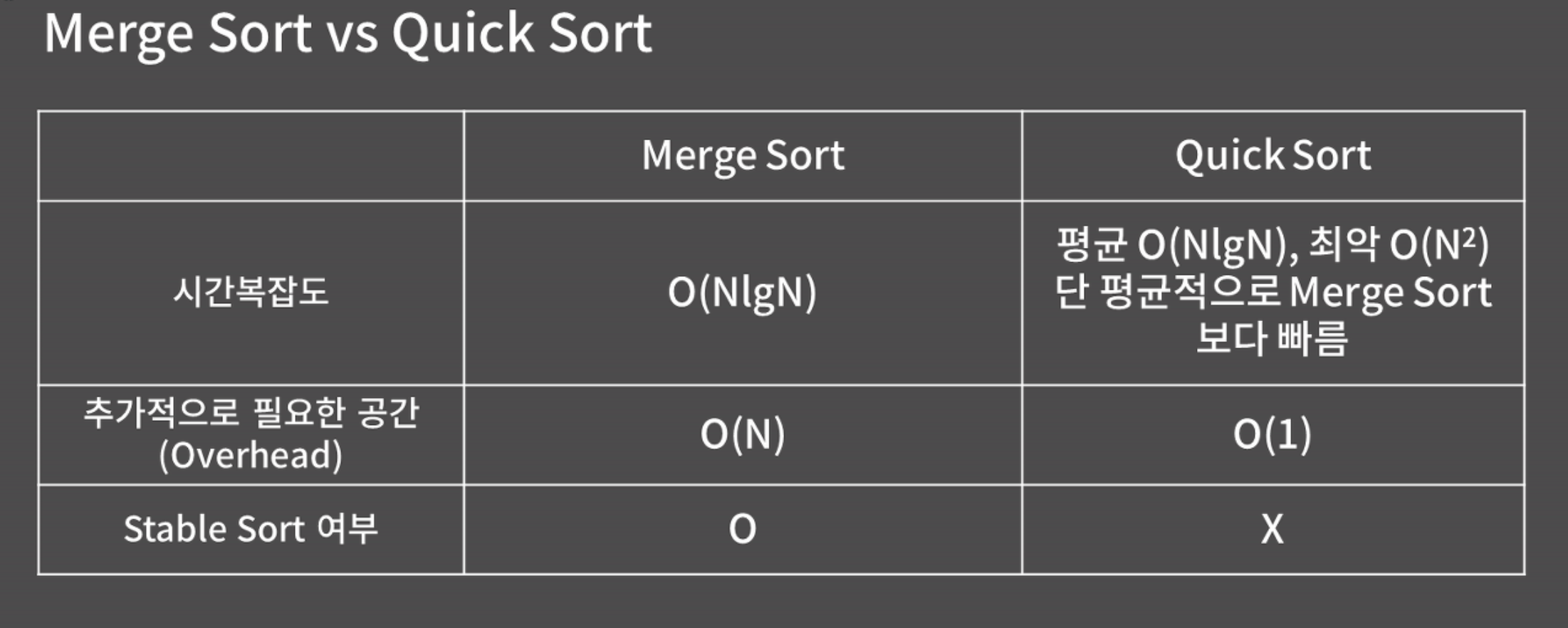

카운팅 정렬 - O(N+K)

각 수의 등장 횟수를 이용하는 정렬

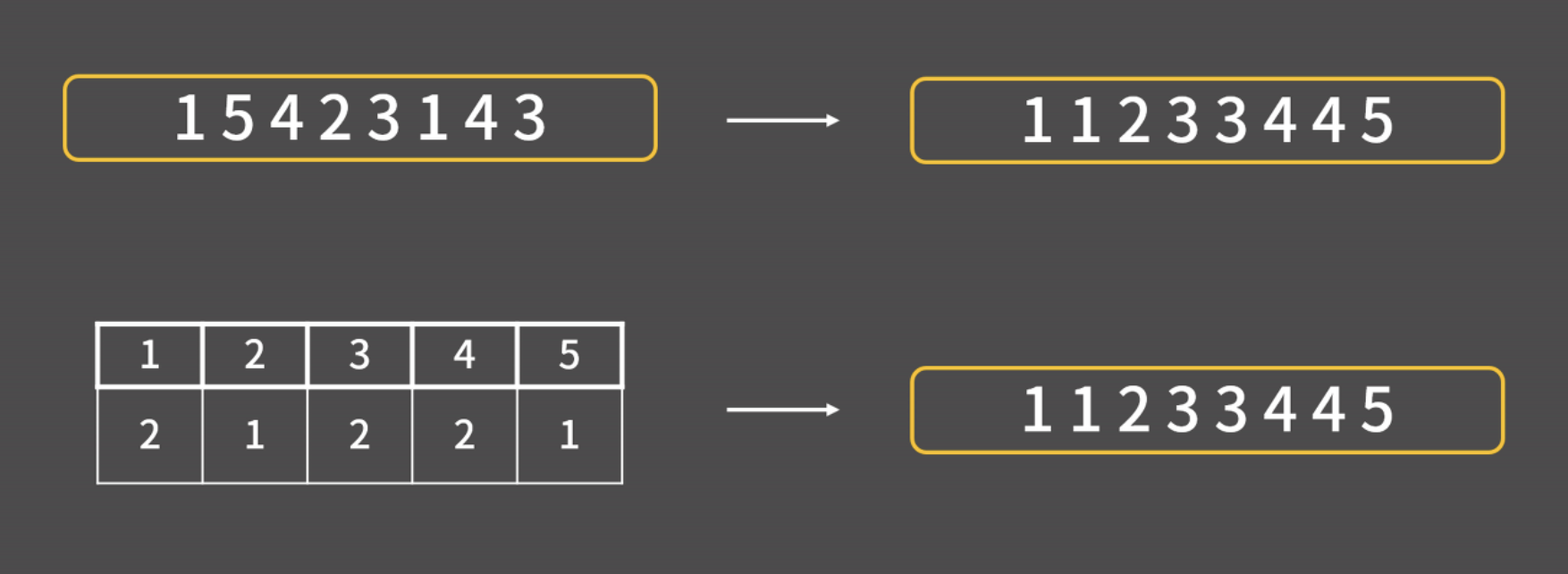
미리 큰 테이블을 만들어두고, 수에 대응되는 원소의 값을 1 증가시켜서 처리하기 때문에 수의 범위가 어느정도 한정적일 때만 사용할 수 있음

기수 정렬(Radix Sort) - O(DN)

자릿수를 이용하는 정렬

1. 수열에서 수를 하나씩 읽으면서 1의 자리에 따라 수 넣기 -> 수를 다시 꺼내서 재배열

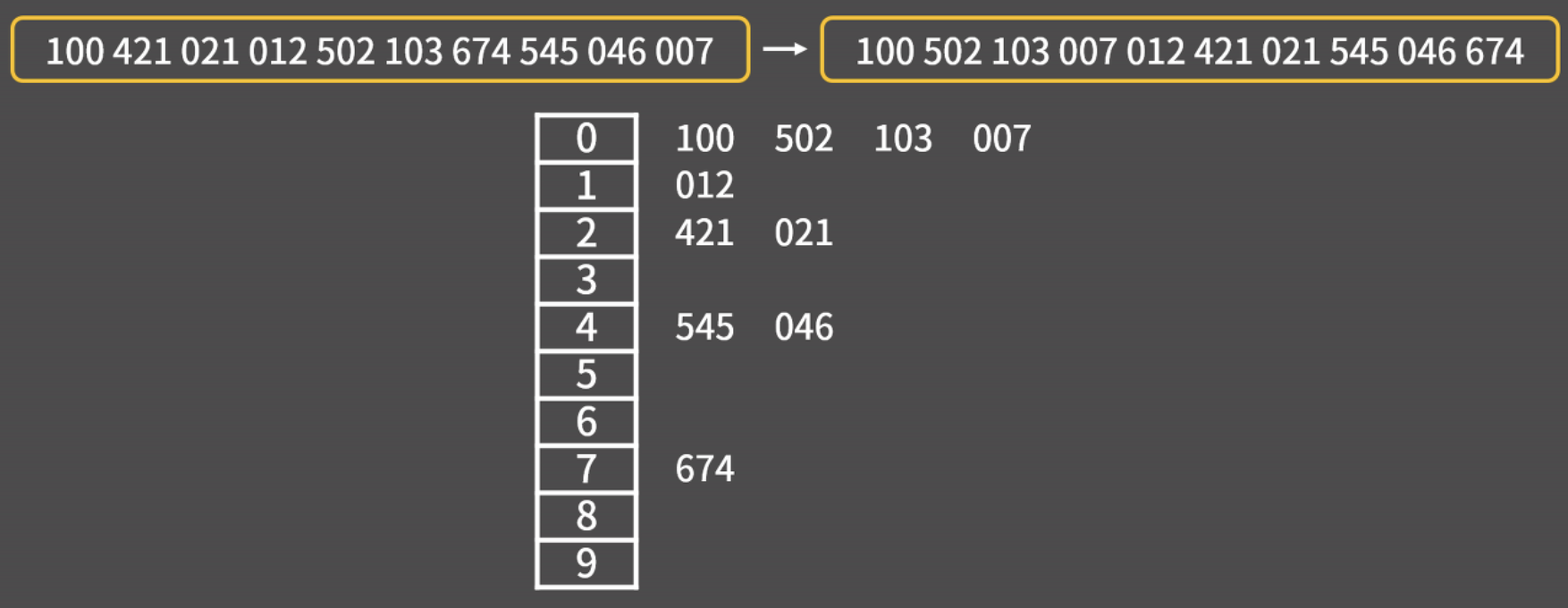
2. 1의 자리를 기준으로 정렬된 리스트를 다시 10의 자리로 정렬 -> 수를 다시 꺼내서 재배열
3. 100의 자리도 마찬가지로 정렬

위상 정렬

• 사이클이 없는 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것
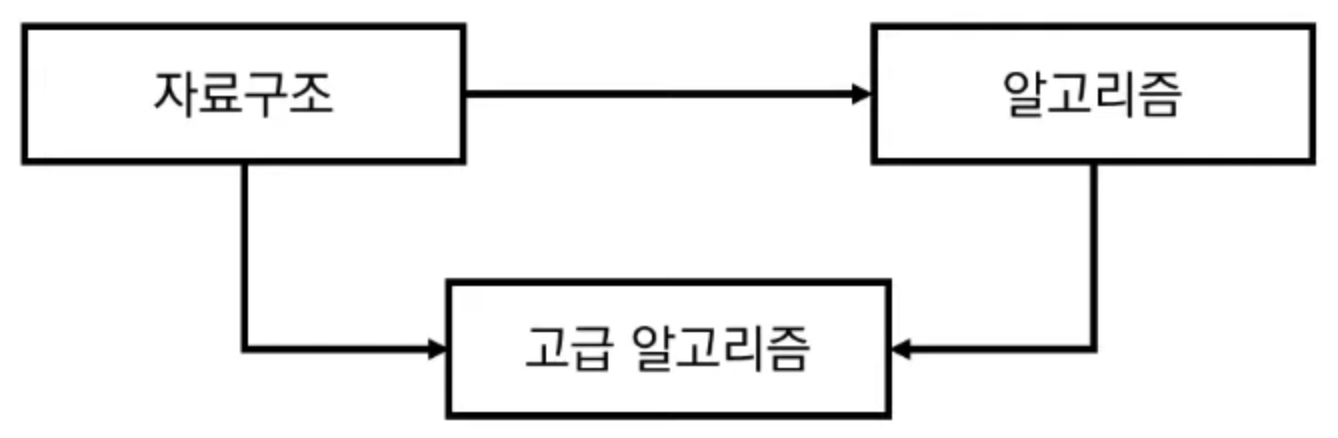
• ex) 선수과목을 고려한 학습 순서 설정: 자료구조 -> 알고리즘 -> 고급 알고리즘 순으로 수강해야 함
  

• 큐를 이용한 위상 정렬 알고리즘의 구현
  1) 진입차수가 0인 모든 노드를 큐에 넣음
  2) 큐가 빌 때까지 다음 과정을 반복함 -> 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거함 + 새롭게 진입차수가 0이 된 노드를 큐에 넣음
  -> 결과적으로 각 노드가 큐에 들어온 순서가 위상정렬을 수행한 결과와 같음
  

from collections import deque

indegree = [0] * (v + 1)   # 모든 노드에 대한 진입차수
graph = [[] for _ in range(v+1)]    # 각 노드에 연결된 간선 정보

# 방향 그래프의 모든 간선 정보를 입력 받기
for _ in range(e):
	a, b = map(int, input().split())
    graph[a].append(b)   # 정점 A에서 B로 이동 가능
    indegree[b] += 1
    
# 위상정렬 함수
def topology():
	answer = []    # 위상정렬 수행 결과
    q = deque()
    
    for i in range(1, v+1):
    	if indegree[i] == 0:
        	q.append(i)   # 진입차수가 0인 노드를 큐에 삽입
            result[i] = time[i]
    
    while q:
    	now = q.popleft()
        answer.append(now)
        
        # 해당 원소와 연결된 노드들의 진입차수에서 1 빼기 
        for i in graph[now]:
        	indegree[i] -= 1
            result[i] = max(result[i], result[now] + time[i])    # 건물 짓는데 드는 최소 시간
            if indegree[i] == 0:   # 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
            	q.append(i)

2️⃣ 코드

입출력

• input 대신 sys.stdin.readline을 사용할 수 있음

import sys

case = int(sys.stdin.readline())
p, q = map(int, sys.stdin.readline().split())


# 입력 개수를 모를 때 
while True:
	try:
    	time, name = input().split()
    except:
    	break

​

• print(a, b, sep=':') -> a:b
• print 개행 제거 -> print(, end='')

​

정렬 조건

# 내림차순 정렬
list.sort(reverse=True)

# 정렬 조건 추가
arr = sorted(arr, reverse=True, key=lambda x:(x[0].lower(), int(x[1])))

3️⃣ 문제 풀이

* 프로그래머스 인사고과 (Lv 3)

https://school.programmers.co.kr/learn/courses/30/lessons/152995

어떤 사원의 근무 태도 점수와 동료 평가 점수가 다른 사원보다 모두 낮으면 인센티브를 받지 못할 때, 완호(scores[0])의 등수 구하기
​

def solution(scores):
    answer = 1

    yanho = scores[0]
    scores.sort(key=lambda x: (-x[0], x[1]))

    temp = 0
    for i in range(len(scores)):
        if yanho[0] < scores[i][0] and yanho[1] < scores[i][1]:
            return -1

        # 이렇게 하면 인센티브를 받지 못하는 사람은 아예 세지 않음 
        if temp <= scores[i][1]:
            # 완호보다 점수가 더 큰 사람이 있으면 완호의 등수가 내려감 
            if sum(yanho) < scores[i][0] + scores[i][1]:
                answer += 1
            temp = scores[i][1]
            
    return answer

직원 전체에 대해 값을 구할 필요가 없이 완호만 신경쓰면 된다!!

​

❓아래처럼 풀면 틀리는 이유

scores.sort(reverse=True)

for i in range(len(scores)):
	a, b = scores[i]
	if a > yanho[0] and b > yanho[1]:
		answer = -1
		break
        
	if scores[0][0] > a and scores[0][1] > b:
		continue 

	if a + b > sum(yanho):
		answer += 1

[[7, 1], [6, 6], [6, 6], [5, 4], [5, 4]]의 경우, [6,6]>[5,4]라 인센티브를 받지 못하지만 1<4라 제외되지 않는다(오류)