03. 힙 정렬

힙(heap)이란?

힙은 완전 이진 트리(Complete Binary Tree)의 일종으로 부모 노드와 자식 노드 간에 특정한 조건을 만족하는 자료구조를 뜻한다.

완전 이진 트리란, 부모 노드 밑에 자식 노드가 최대 2개까지 있을 수 있고, 마지막 레벨을 제외한 모든 노드에 노드가 완전히 채워진 트리 구조이다.

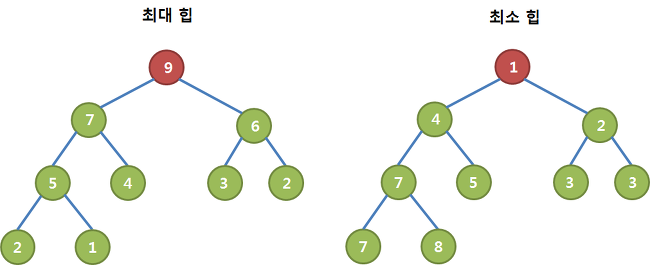
힙의 종류에는 최대 힙(Max-heap), 최소 힙(Min-heap)이 있다. 최대 힙은 부모 노드가 자식 노드보다 값이 크거나 같은 것을 의미하고, 최소 힙은 부모 노드가 자식 노드보다 값이 작거나 같은 것을 의미한다.

이러한 특성으로 인해 최대 힙의 루트 노드는 전체 힙 중 가장 큰 값을 가지고, 최소 힙의 루트 노드는 전체 힙 중 가장 작은 값을 가진다.

힙 코드 구현

힙은 보통 배열(Array)를 이용해서 구현한다. 루트 노드는 배열의 첫 번째 인덱스에 위치한다. 그러므로 인덱스가 1부터 시작하는 배열의 경우, 왼쪽 자식 노드는 2i, 오른쪽 자식 노드는 2i+1에 위치한다.

public class HeapStudy {

    public int[] heap;
    public int size;
    
    //힙 구축
    public void build_min_heal(int[] arr){
        this.size = arr.length;
        this.heap = new int[size+1];

        System.arraycopy(arr,0,heap,1,size);

        for(int i=size/2;i>=1;i--){
            min_heapify(i);
        }
    }

    public void min_heapify(int i){
        int left = 2*i;
        int right = 2*i+1;
        int smallest;
        
        //왼쪽 자식 노드와 비교
        if(left<size&&heap[left]<heap[i]){
            smallest = left;
        }else{
            smallest = i;
        }
        
        //위에서 비교한 값과 오른쪽 자식 노드와 비교
        if(right<size&&heap[right]<heap[smallest]){
            smallest = right;
        }
        
        //자식 노드가 더 작으면 위치를 바꾸고, min_heafify 재귀 호출
        if(smallest!=i){
            swap(i, smallest);
            min_heapify(smallest);
        }
    }
    
    //위치 바꾸기
    public void swap(int i, int j){
        int temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }

    public void printHeapArray(){
        for(int i=1; i<=size; i++){
            System.out.print(heap[i]+" ");
        }
        System.out.println();
    }
}

앞서, 힙 정렬은 배열로 푼다고 언급했는데 특정한 경우 큐와 스택을 함께 사용하면 효율성이 증가한다.

다음은 프로그래머스의 더 맵게 문제 풀이 예제이다.

public class MoreSpicy {
    public int solution(int[] scoville, int K) {
        // PriorityQueue를 사용하여 최소 힙을 구현
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();

        // 모든 스코빌 지수를 최소 힙에 추가
        for (int s : scoville) {
            minHeap.add(s);
        }

        int answer = 0;

        // 최소 힙의 최솟값이 K 이상이 될 때까지 반복
        while (minHeap.peek() < K) {
            // 최소 힙에 요소가 2개 미만인 경우 모든 음식의 스코빌 지수를 K 이상으로 만들 수 없음
            if (minHeap.size() < 2) {
                return -1;
            }

            // 가장 맵지 않은 음식 두 개 꺼내기
            int first = minHeap.poll();
            int second = minHeap.poll();

            // 새로운 스코빌 지수를 계산하여 다시 최소 힙에 추가
            int newScoville = first + (second * 2);
            minHeap.add(newScoville);

            // 섞은 횟수 증가
            answer++;
        }

        return answer;
    }
}