
“You can’t connect the dots looking forward; you can only connect them looking backwards. So you have to trust that the dots will somehow connect in your future. You have to trust in something — your gut, destiny, life, karma, whatever. This approach has never let me down, and it has made all the difference in my life.”
센치한 저녁 포스팅. (개인적으로 좋아하는) 유명한 연설로 시작. 🐳
Steve Jobs 말씀하시길, 과거를 뒤돌아 볼때만 Connecting the dots 할 수 있다고 했다. 과거의 우연한 일이 오늘이나 미래의 나에게 어떤 의미를 가지는지, 그 당시로서는 알 수 없지만 내가 무작위로 찍어온 모든 방점들은 결국은 연결된다. 백지 위에 찍은 점들이 일직선이진 않지만, 나는 그 점들을 이을 수 있다. 그게 바로 이번에 소개하는 Graph 의 모양과 같다. Tree, Binary Search Tree 도 크게 보면 Graph에 속한다.
🙋🏻♀️ Graph 자료 구조의 특징은요?
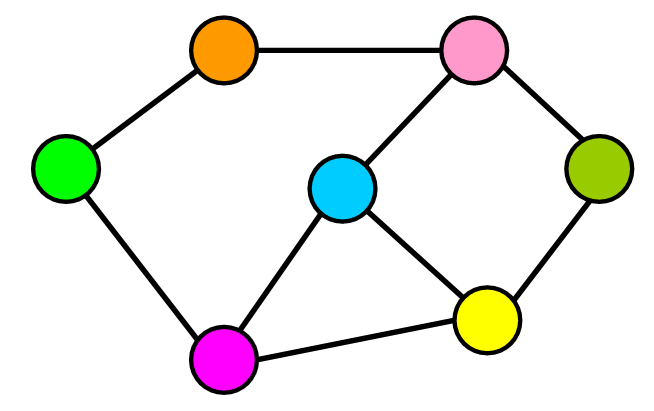
그림으로 본다면, 그래프는 이렇게 정점(vertext)과 간선(edge)으로 이루어진 형태이고, 각 정점이 바로 데이터를 상징한다.
- 방향성이 있는 그래프 (Directed graph)
간선이 A -> B 만 보고있는 방향성이 있는 형태. A -> B 한쪽으로만 연결된 상태에서 당연히 B에서 A로는 갈 수 없다.
🍊 여기서 인앤아웃 개념을 적용해볼 수 있는데, 간선이 들어오면indegree, 간선이 나가면outdegree라고 부른다.
예를 들어, A <- B -> C 의 방향그래프에서, A, C 는 각각 1개의 indegree 를 가지고, B는 2개의 outdegree를 가진다.- 방향성이 없는 그래프 (Undirected graph)
간선이 A <-> B 양쪽을 잇는 방향성이 없는 형태.- 간선이 A -> A 로 오는, Self Loop 가능
- 간선이 A -> B -> C -> A 로 오는, Loop Circuit 가능
- 간선에 가중치 부여해서 가중치 그래프(Weighted graph) 가능
🙋🏻♀️ 그래프의 실생활 사례는?
방향성과 가중치를 부여할 수 있으니, 경로 탐색이나 최소 비용 등을 고려해야 할 때 효과적이다.
- 네비게이션
- 지하철 및 버스 노선도
