Data Structure: Graph (2)

그래프를 구현하는 방법에는 대표적으로 두 가지가 있다. 인접행렬과 인접리스트.

🙋🏻‍♀️ 인접행렬 (Adjacency Matrix)?

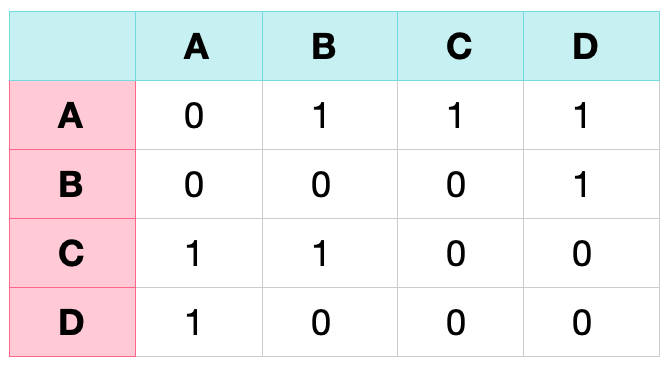
이렇게 A, B, C, D 네 개의 정점으로 매트릭스를 만들어서 연결 관계를 표시한다. 0은 연결 안됨, 1은 연결 됨으로 구분할 수 있다.

[b][b] === 0 // 간선 없음
[c][b] === 1 // 간선 있음

1. 간선 수와 무관하게 n^2 메모리 공간을 차지. 공간복잡도 O(n^2)
2. 간선 유무는 시간복잡도 O(1) 로 찾을 수 있지만,
3. 인접 노드를 찾아야 할 경우, 전체 순회해야 하므로 시간복잡도 O(N)
4. 따라서 간선이 많은 밀집그래프에 유용

🙋🏻‍♀️ 인접리스트 (Adjacency List)?

그래프 구현 시 일반적으로 사용된다. 객체 안에 각 정점이 key 로 들어가게 되고, 그 key 와 연결된 정점들은 모두 value 로 들어간다.

nodes = {
           0: [ 1, 2 ],
           1: [ 0 ],
           2: [ 0 ],
  	   3: [ 2 ]
   	}
/* 위의 인접리스트는 아래와 같은 그래프를 구현하고 있다. 

	0 - 1
 	 \ 2 - 3
    
   0은 1, 2와 연결되어 있고, 3은 2와 연결되어 있다. 
   서로 연결되어 있다면 꼭 서로 저장해주어야 한다. (0과 1처럼)
*/ 

1. n개의 리스트에 간선(E)만큼 요소가 들어있으므로, 공간복잡도 O(V+E)
2. 연결된 인접 노드 시간복잡도 O(1)로 확인 가능
3. 간선이 적은 희소그래프에 유용