대학교 2학년 자료구조 시간에 버블 정렬, 선택 정렬, 삽입 정렬에 대해서 배운 적이 있는데, 지금 설명해 보라고 하면 못할 것 같다..😂 그럼 각각의 차이점을 비교해보고 어떤 기준으로 선택해야 하는지 알아보자!

Sorting에 대해서

"뭔가를 정리하는 것"

사전처럼 A부터 Z까지 기준으로 정렬하거나 큰 수에서 작은 수 기준으로 정렬할 수도 있다. 이진검색처럼 빠른 알고리즘을 사용하려면 일단 먼저 배열 정렬을 해야 한다.

아주 쉬운 3가지 Sorting 알고리즘인 Bubble Sort(버블 정렬), Selection Sort(선택 정렬), Insertion Sort(삽입 정렬)에 대해 알아보자. 가장 빠른 정렬 알고리즘은 아니지만 쉬운 알고리즘이다. 실제로 사람들이 정렬하는 방법과 유사하고 시간 복잡도 계산법도 쉽다.

1. Bubble Sort(버블 정렬)

버블 정렬은 그렇게 좋은 알고리즘이 아니라서 자주 사용되진 않는다. 하지만 이해하기 쉬워서 버블 정렬부터 알아볼 것이다.

버블 정렬은 먼저, 배열에서 2개의 아이템을 선택하고 비교한다.

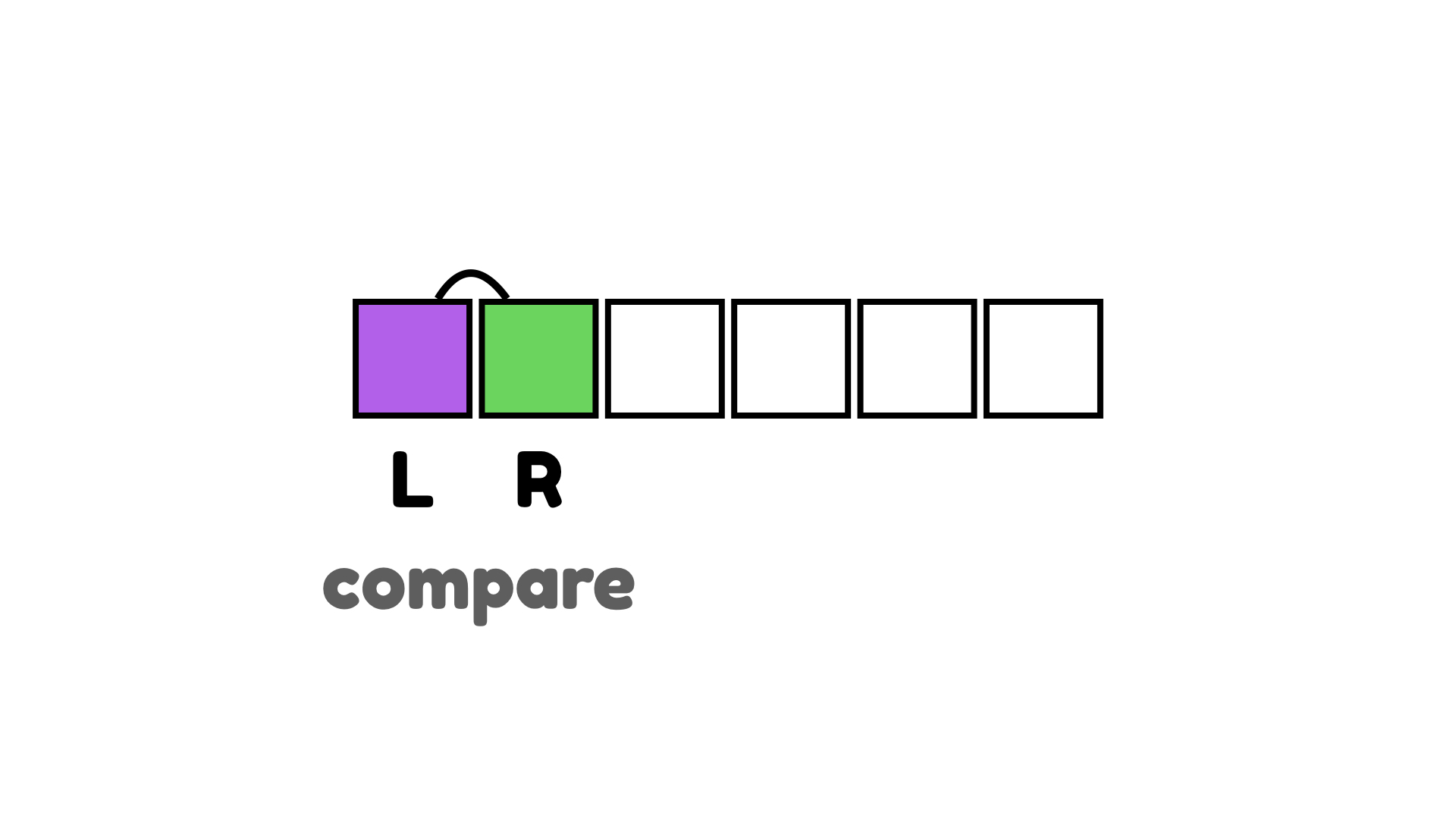
왼쪽이 오른쪽보다 크면 교환한다.

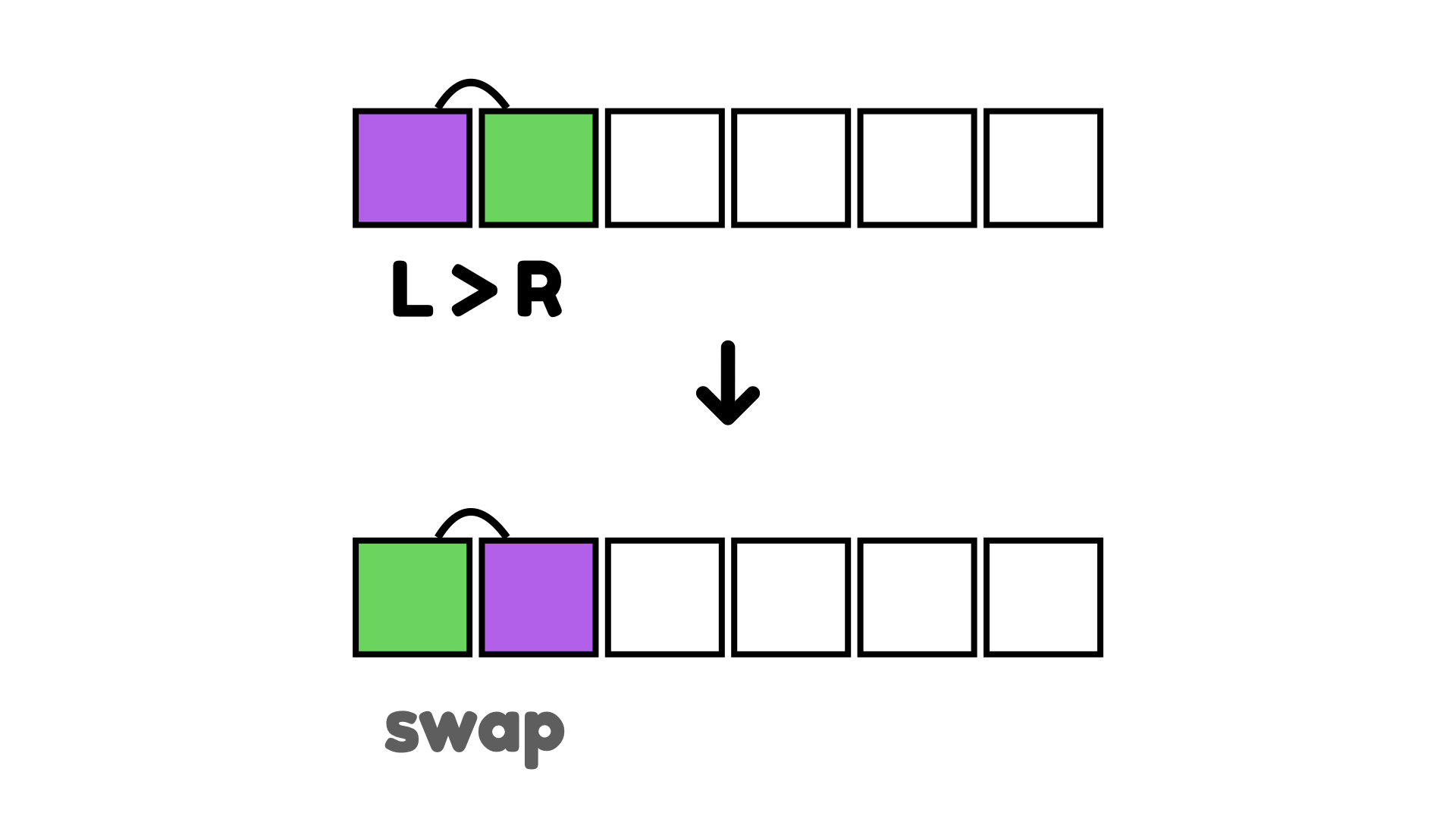
오른쪽으로 이동해서 프로세스를 반복한다.

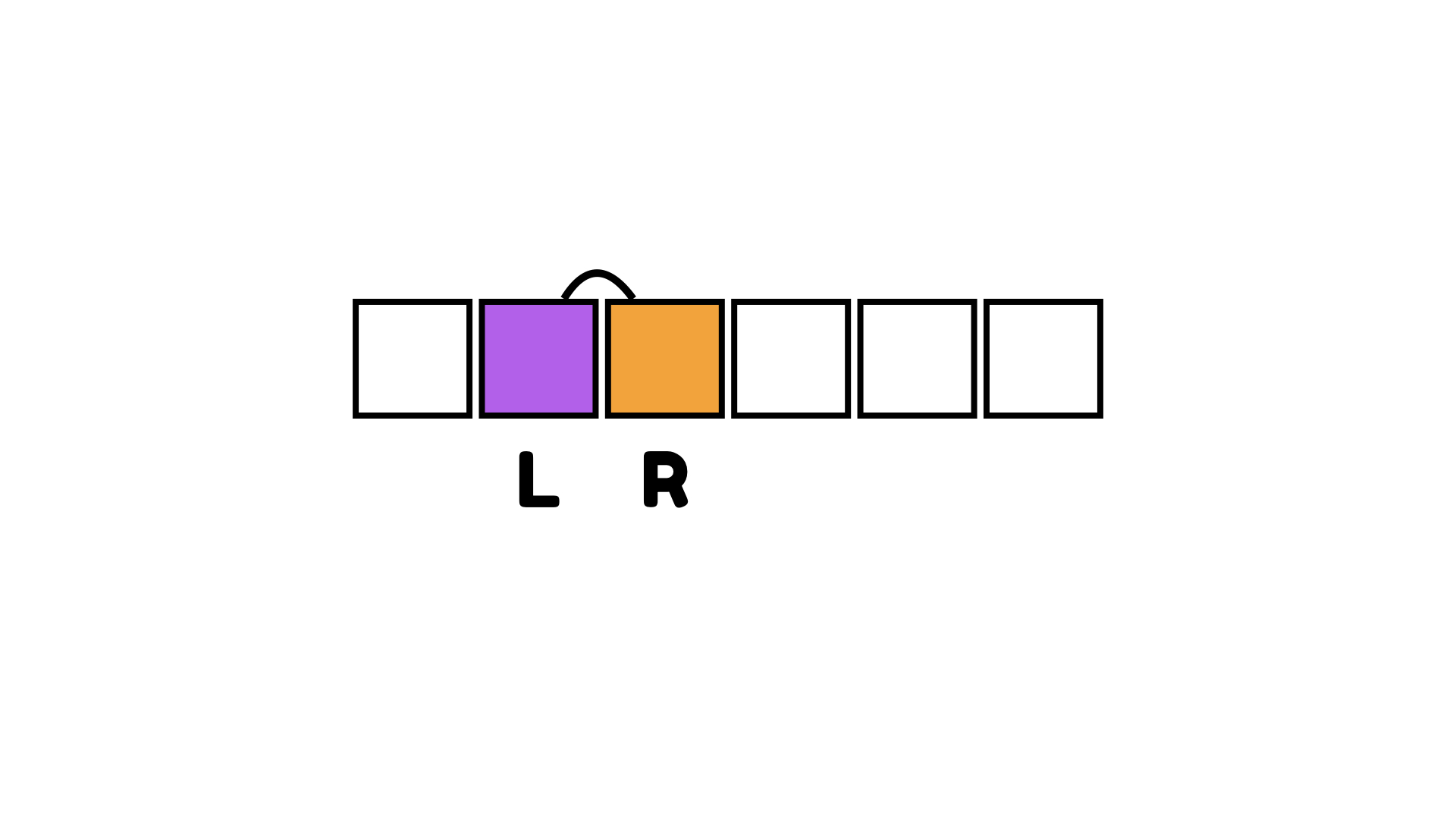
아래 경우에는 5와 2로 시작하는데, 5는 2보다 크니까 교환한다.

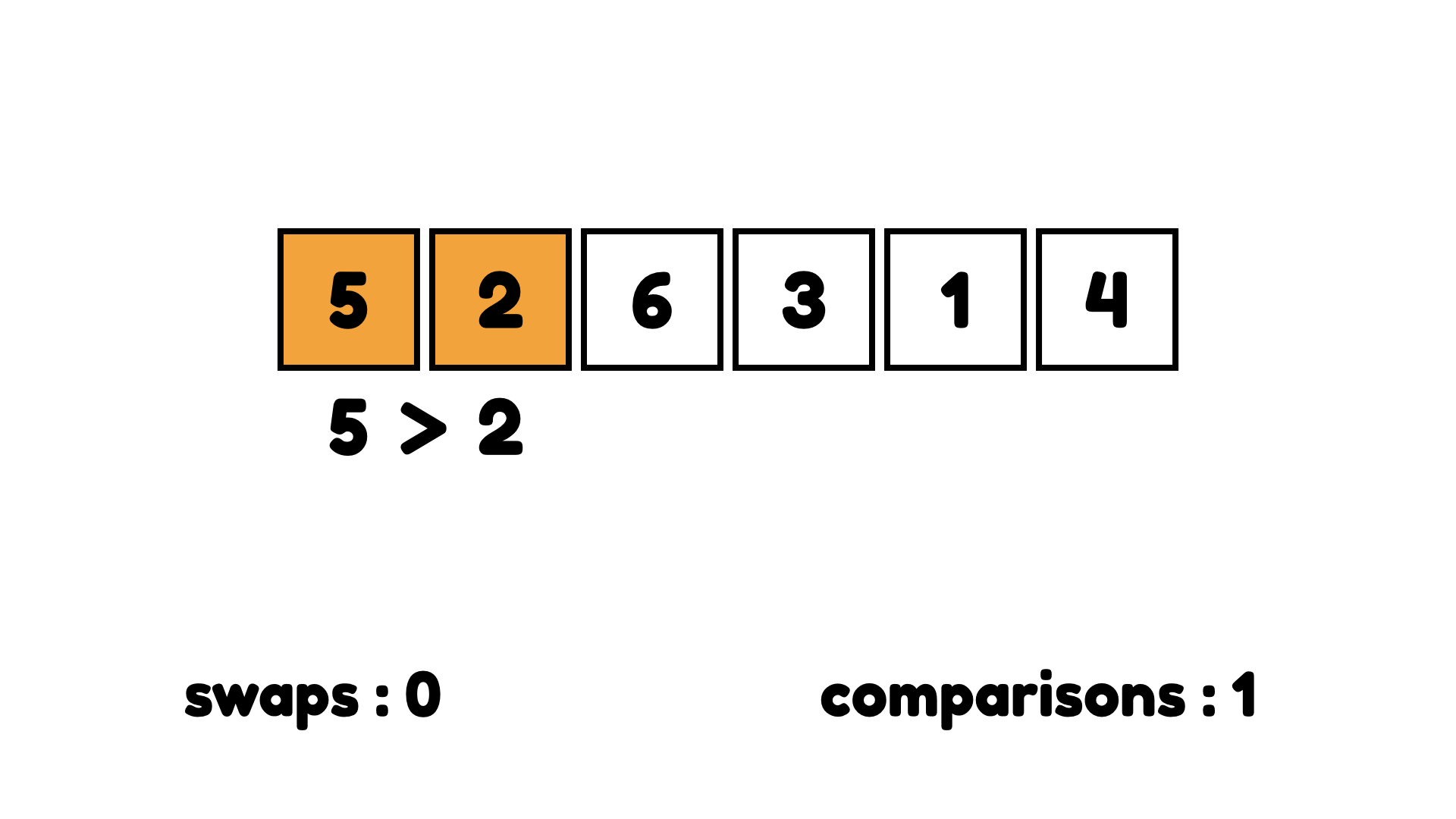
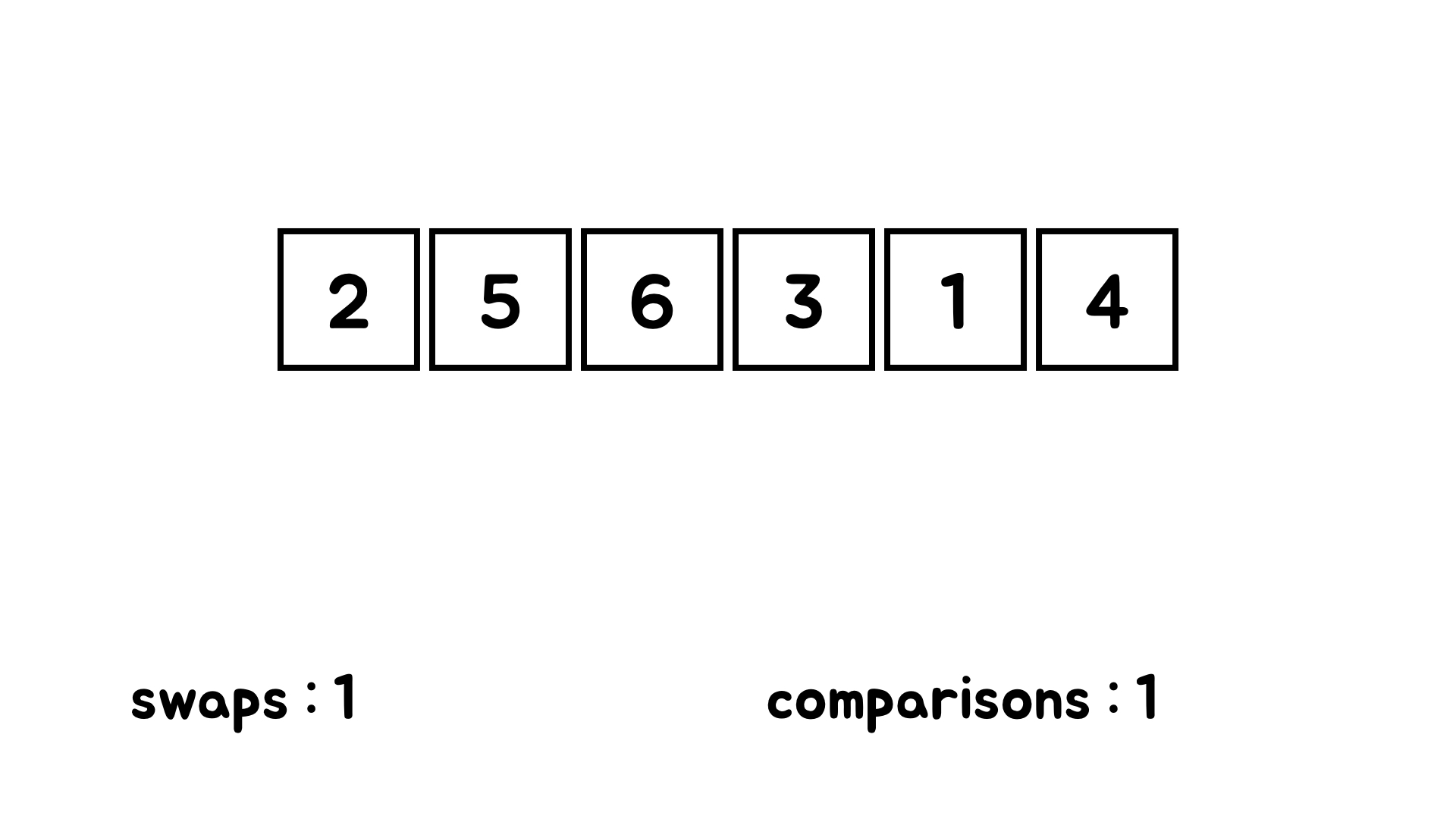
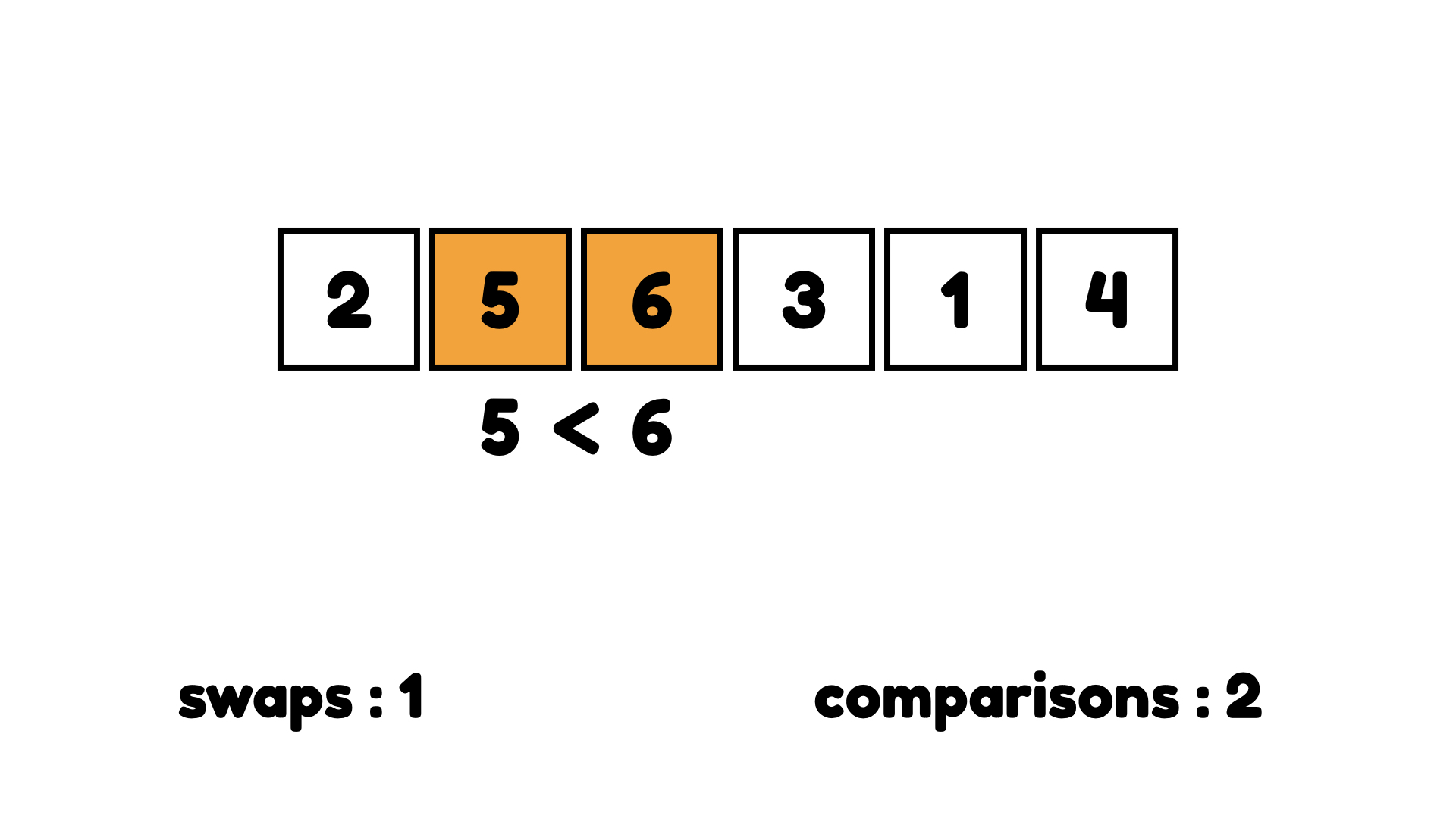
이번엔 오른쪽으로 한 칸 이동해서 5와 6을 비교한다. 5가 더 작으니까 교환하지 않는다.

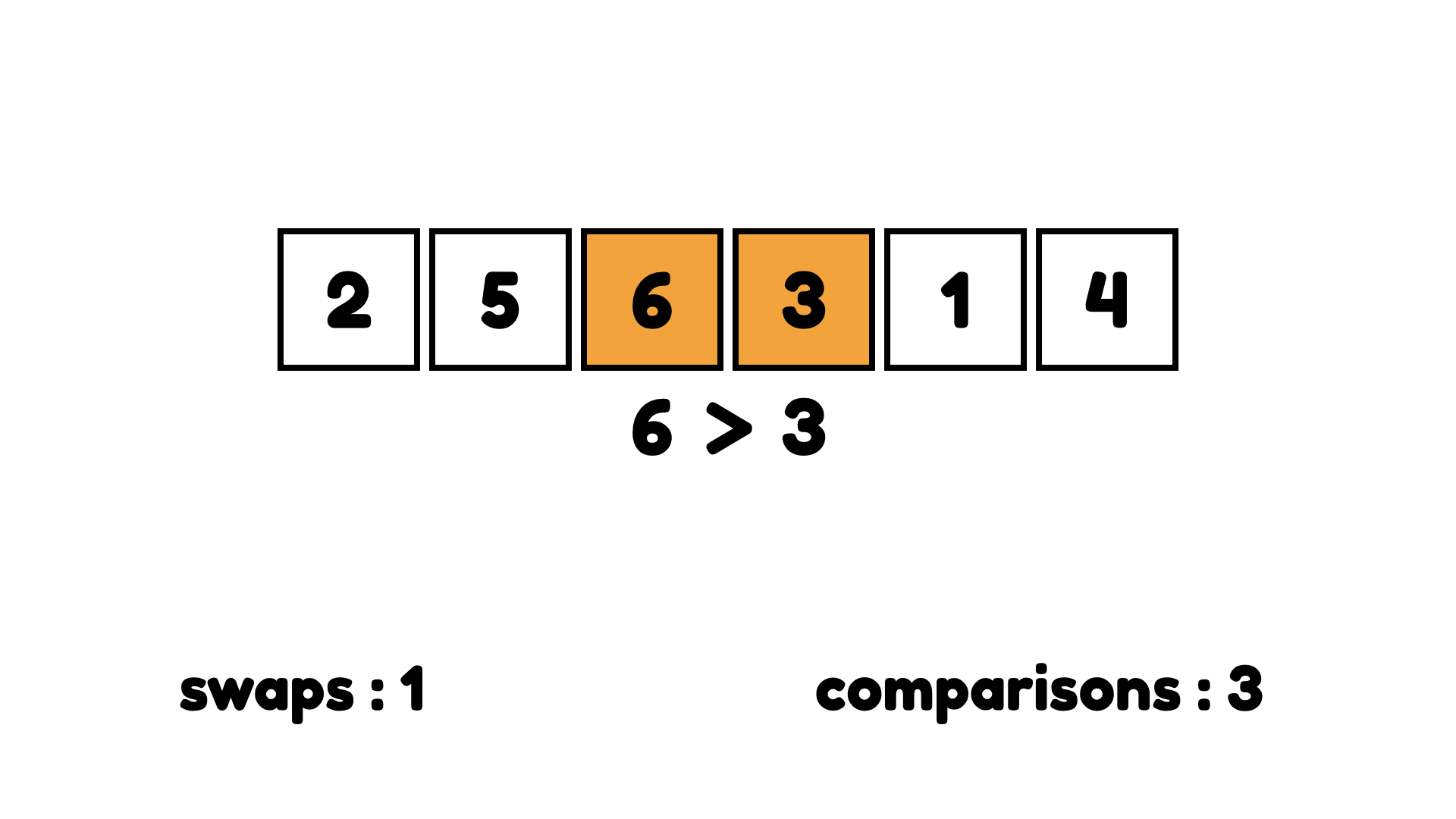
다시 오른쪽으로 한 칸 이동해서 6이 3보다 큰지 비교한다. 크니까 교환한다.

또 오른쪽으로 한 칸 이동해서 6과 1을 비교한다. 6이 더 크니까 교환한다.

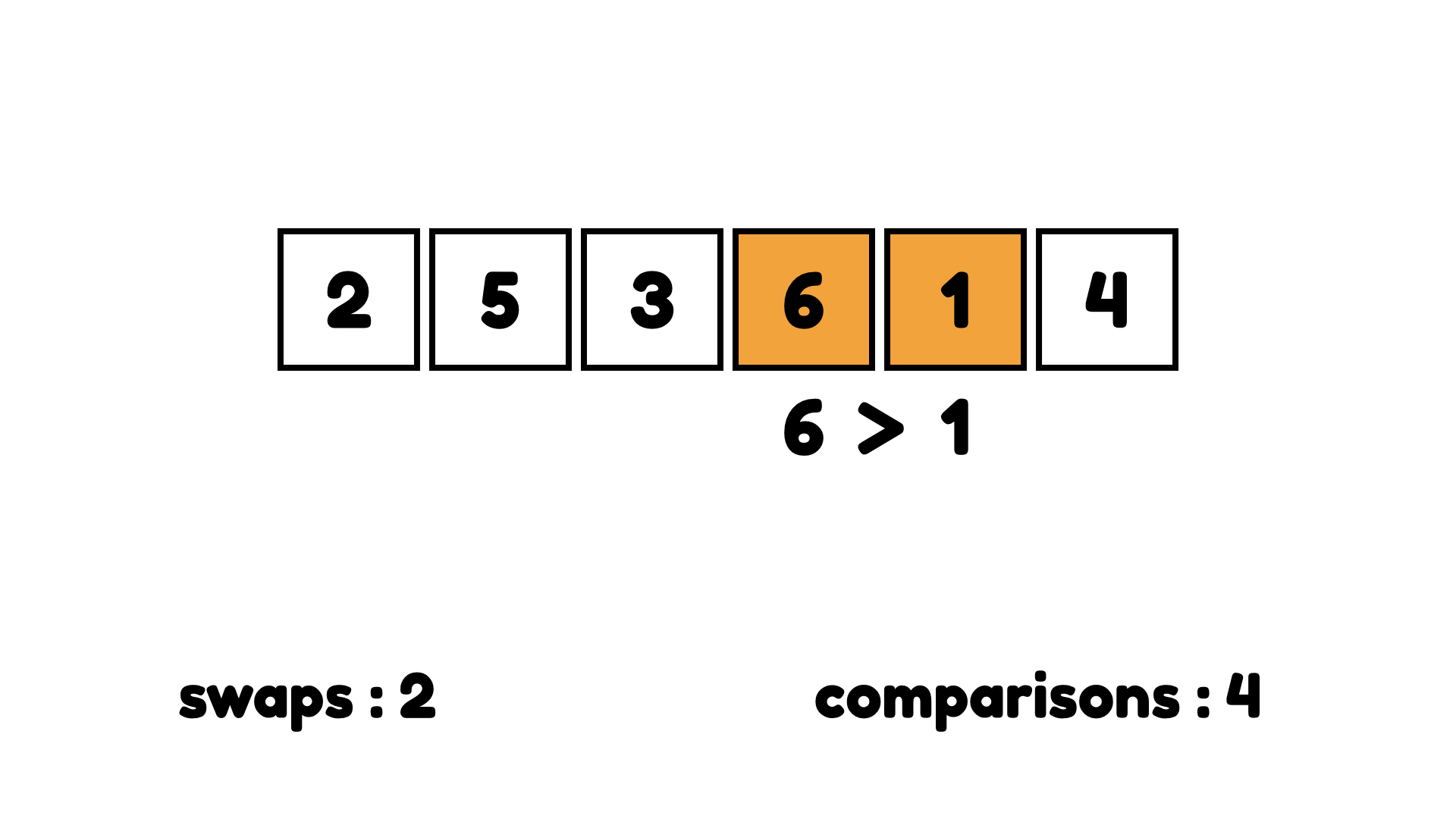
마지막으로 6이 4보다 크므로 교환한다.

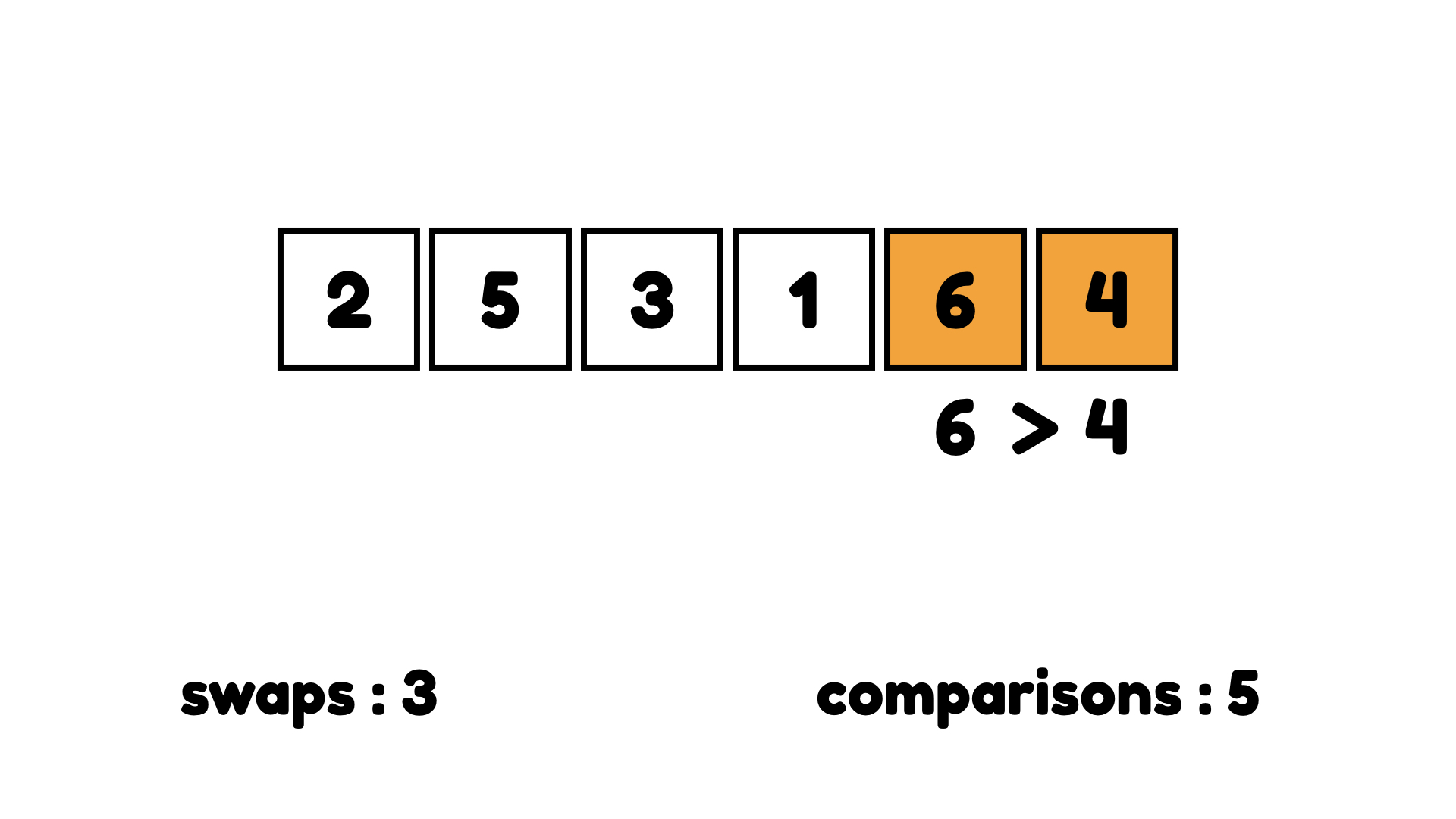
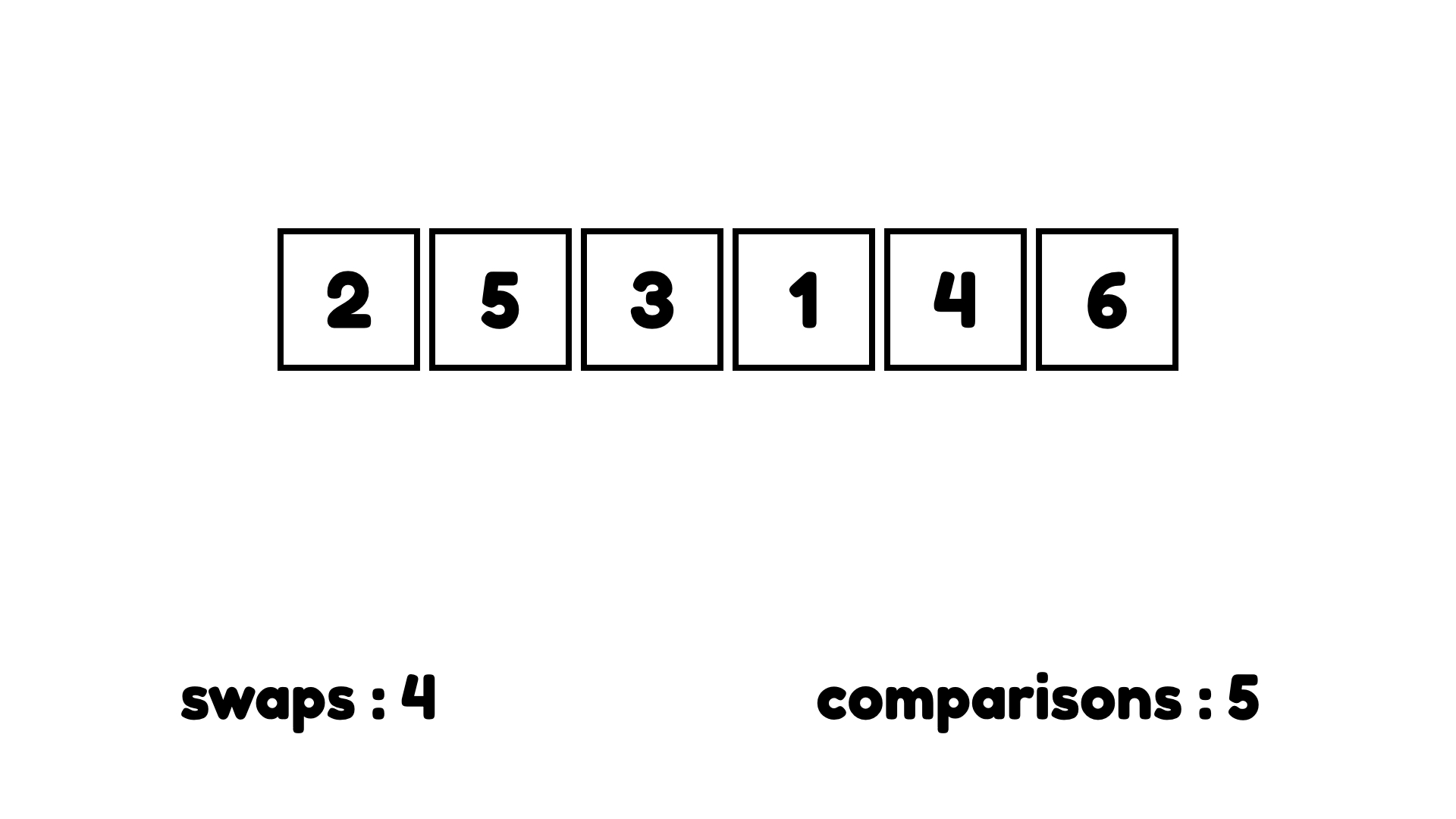
여기까지 버블 정렬의 첫 번째 싸이클이 끝났다. 이렇게 더 큰 아이템이 끝까지 '버블'로 이동하기 때문에 '버블 정렬'이다. 그럼 마저 버블 정렬을 끝내보자.

다시 처음부터 비교해서 2는 5보다 크지 않으므로 교환하지 않는다.

오른쪽으로 이동해서 5는 3보다 크므로 교환한다.

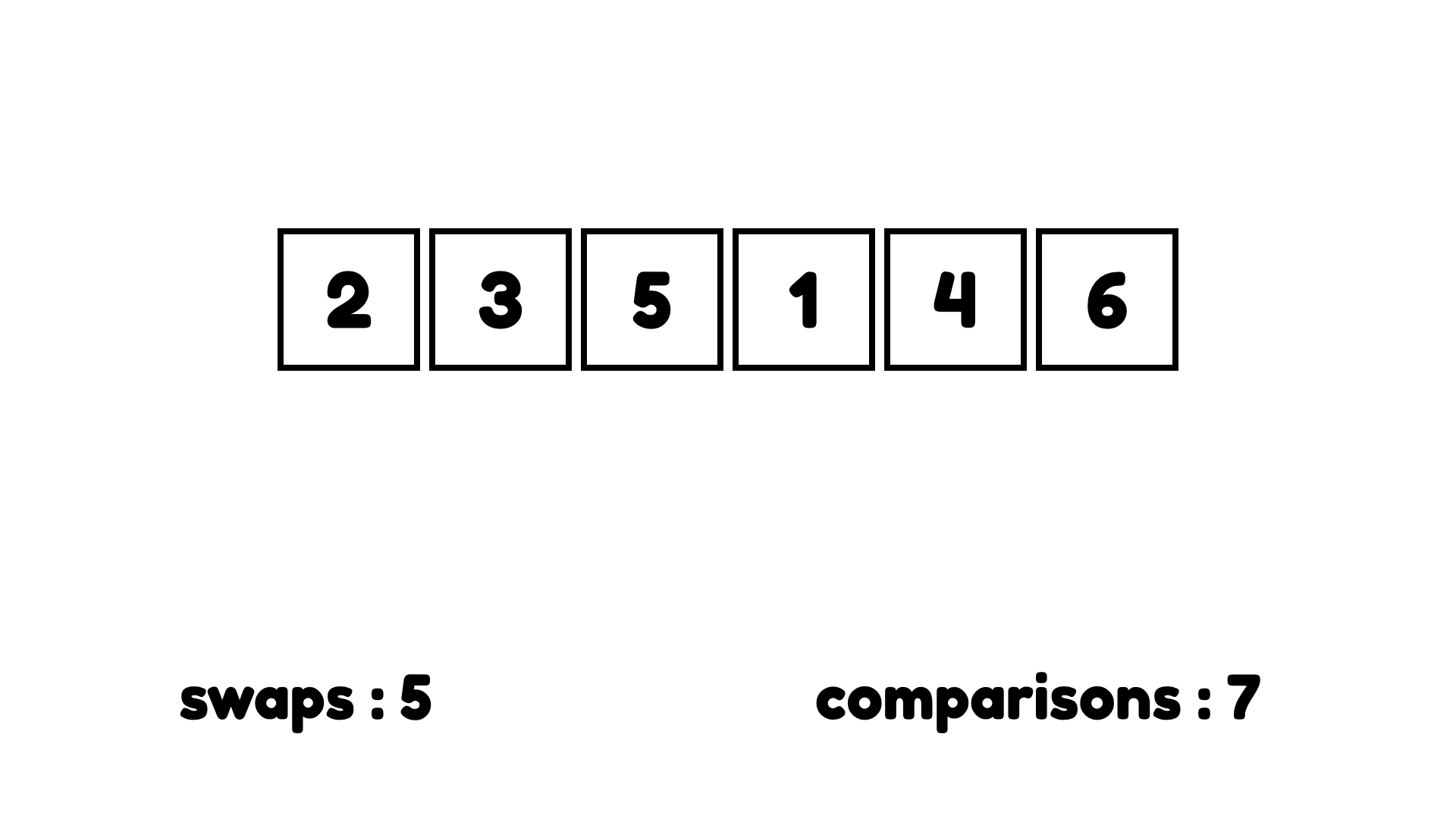
또 오른쪽으로 이동하고 5는 1보다 크므로 교환한다.

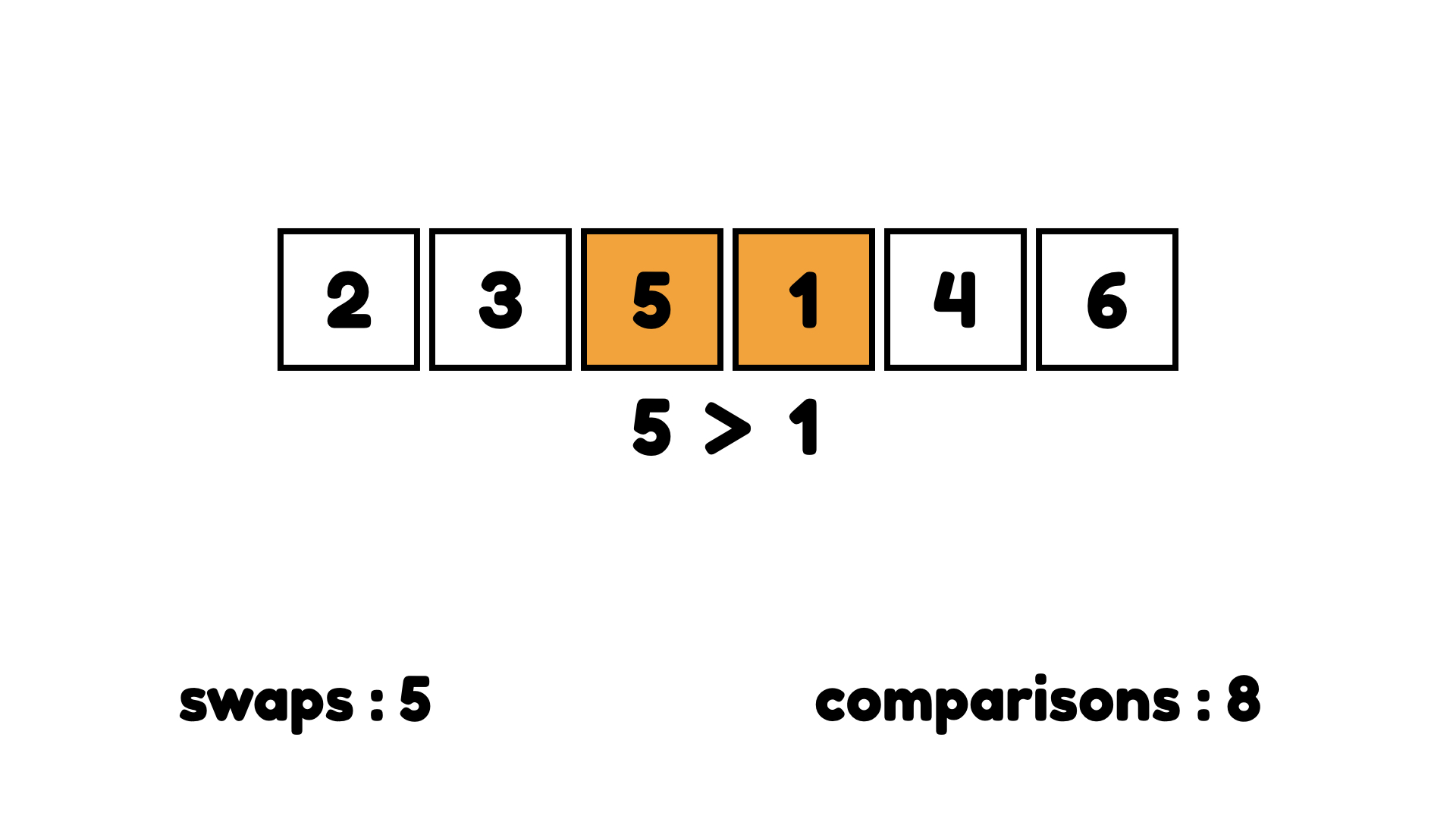
다음 5는 4보다 크므로 교환한다.

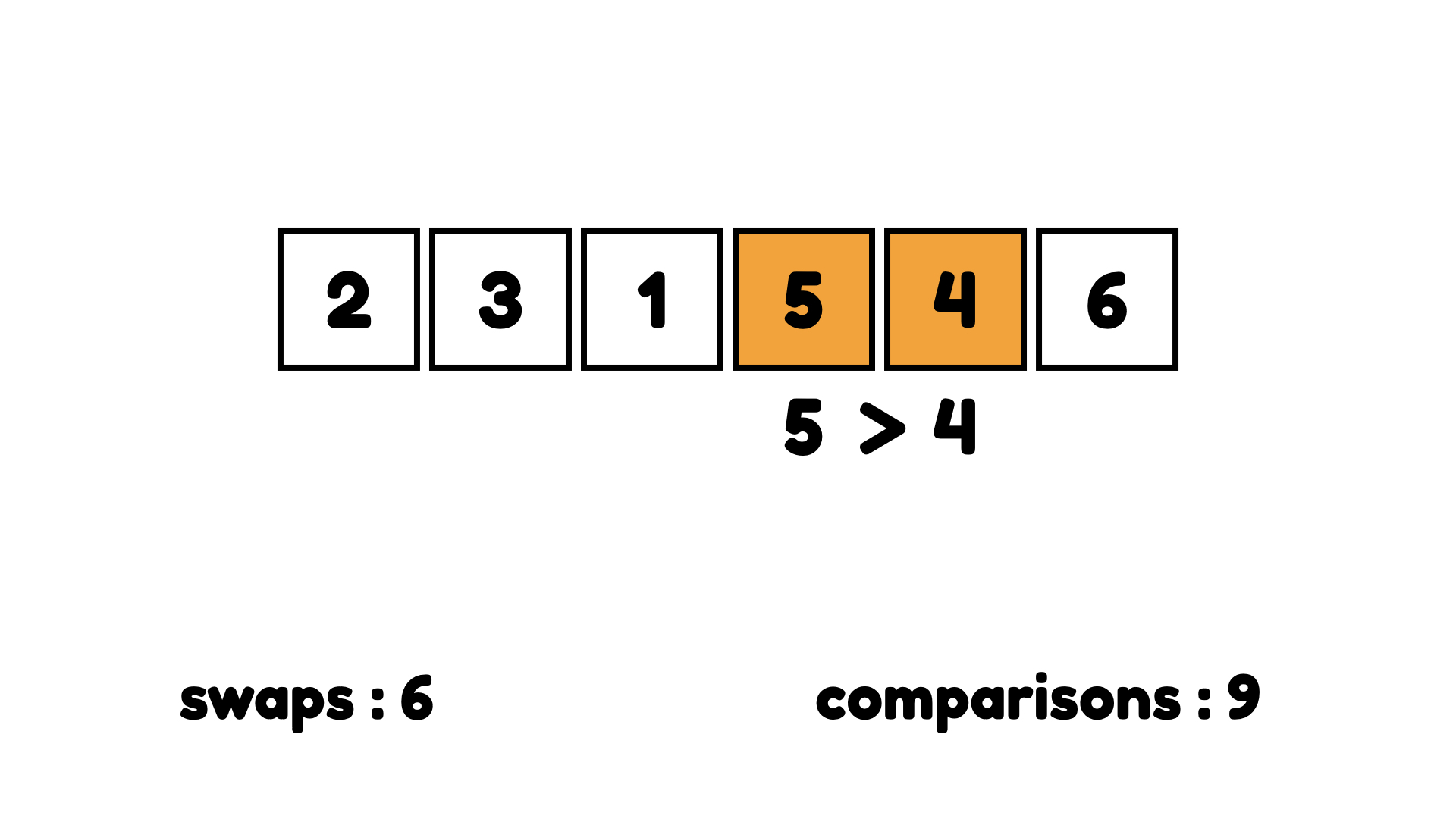
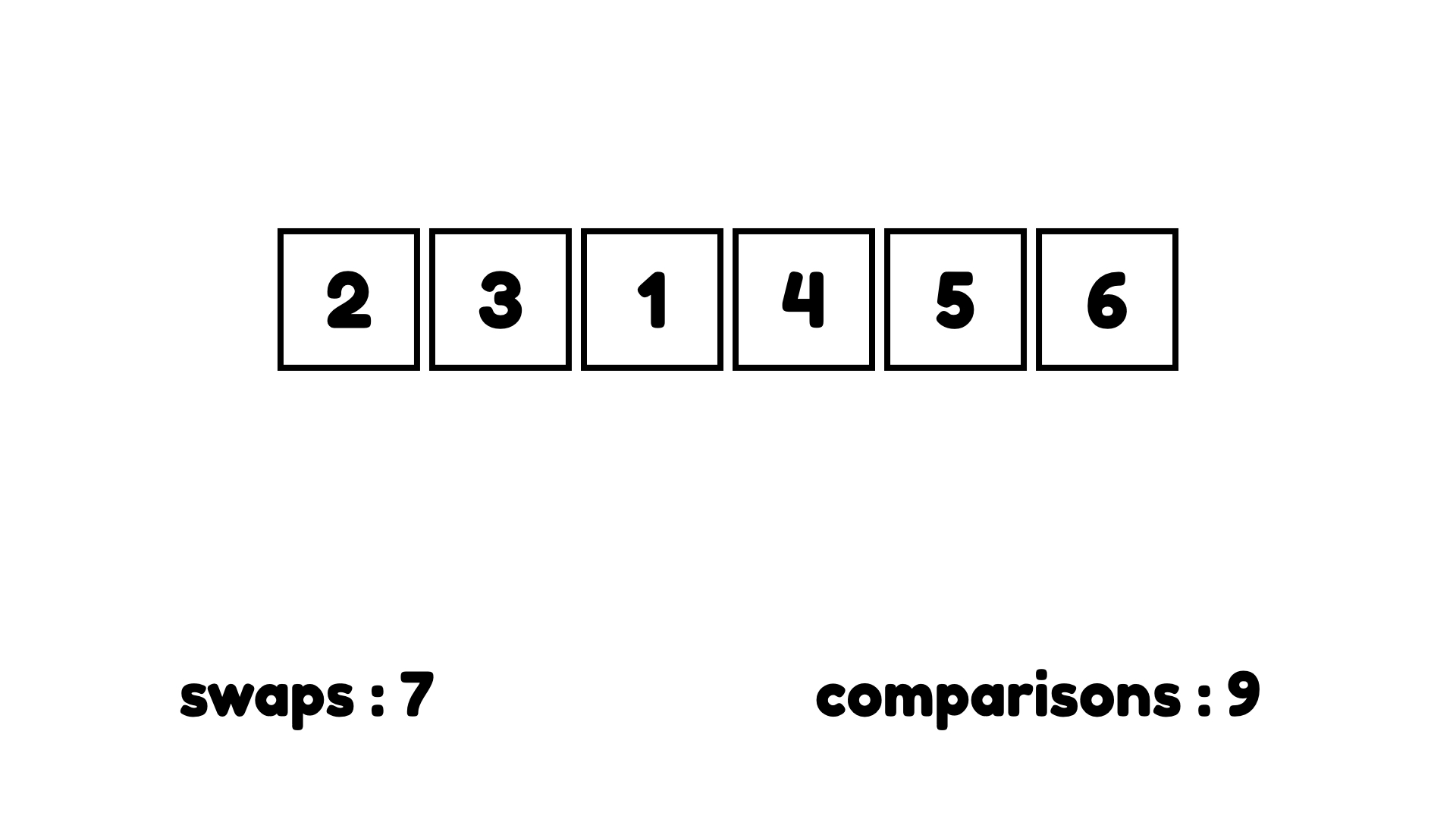
4가 올바른 위치에 도착했다.

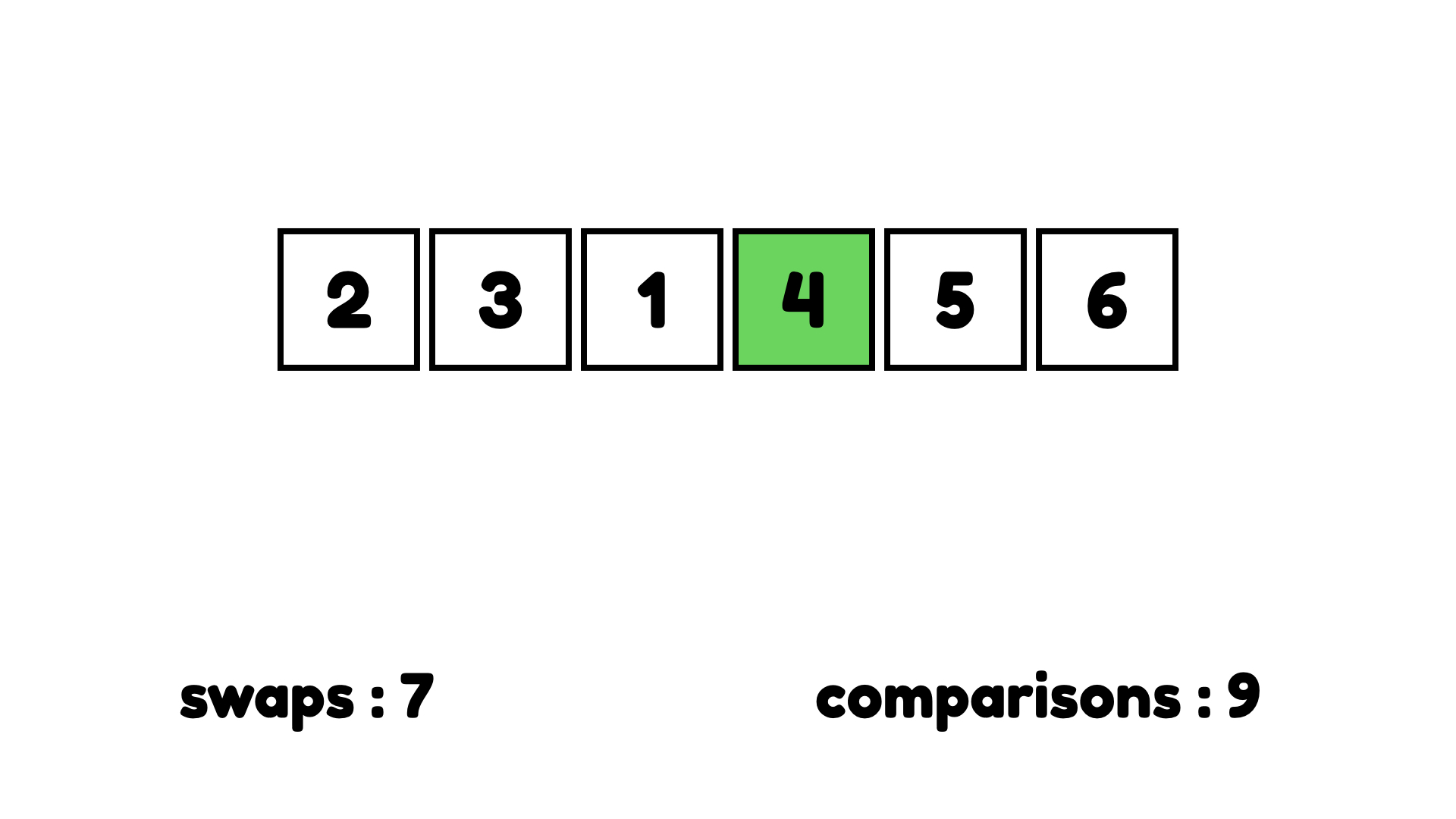
보이는 것 처럼 정말 쉽다. 비교하고 교환하기의 반복이다. 아래가 버블 정렬이 끝났을 때의 모습이다.

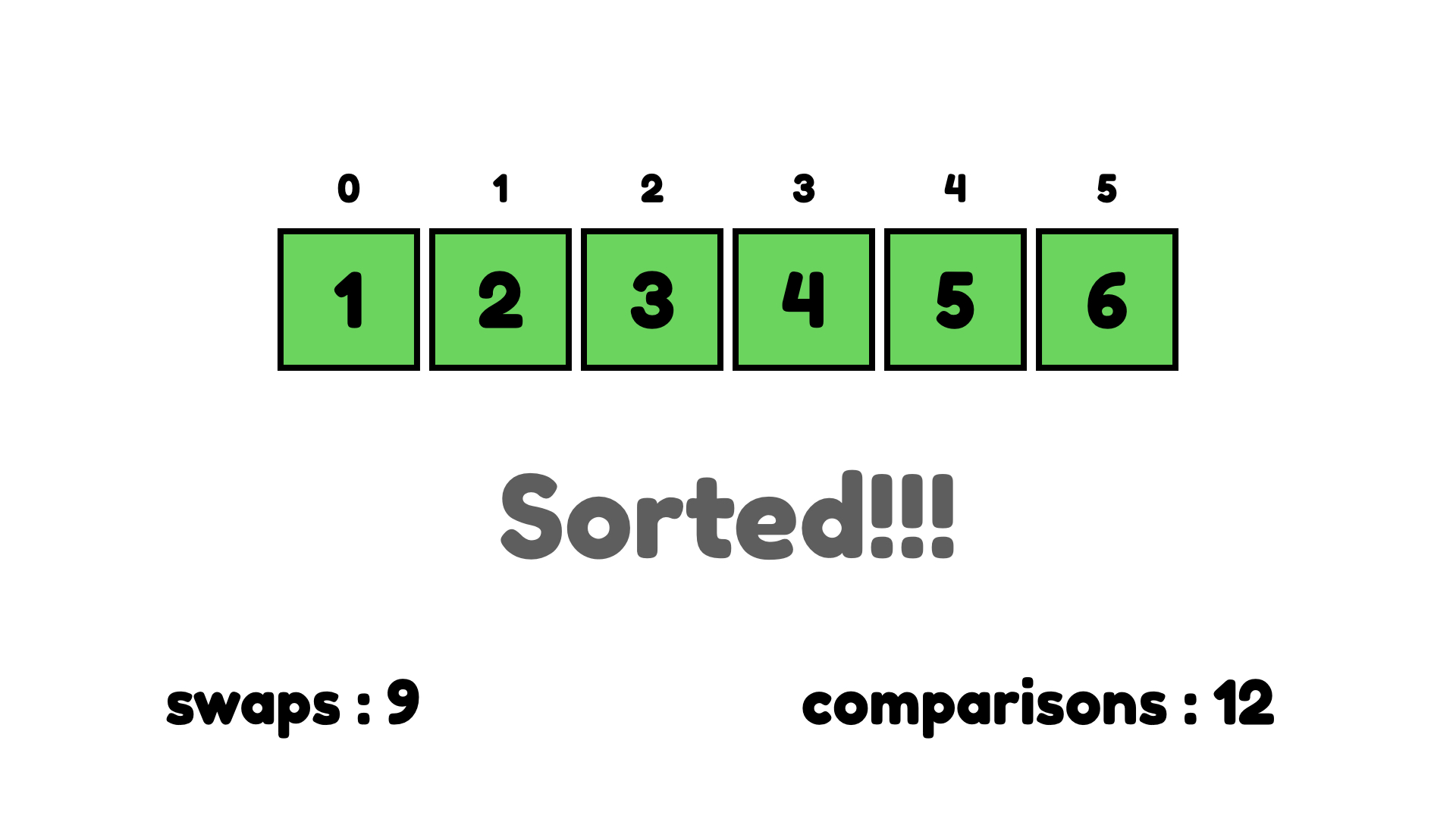
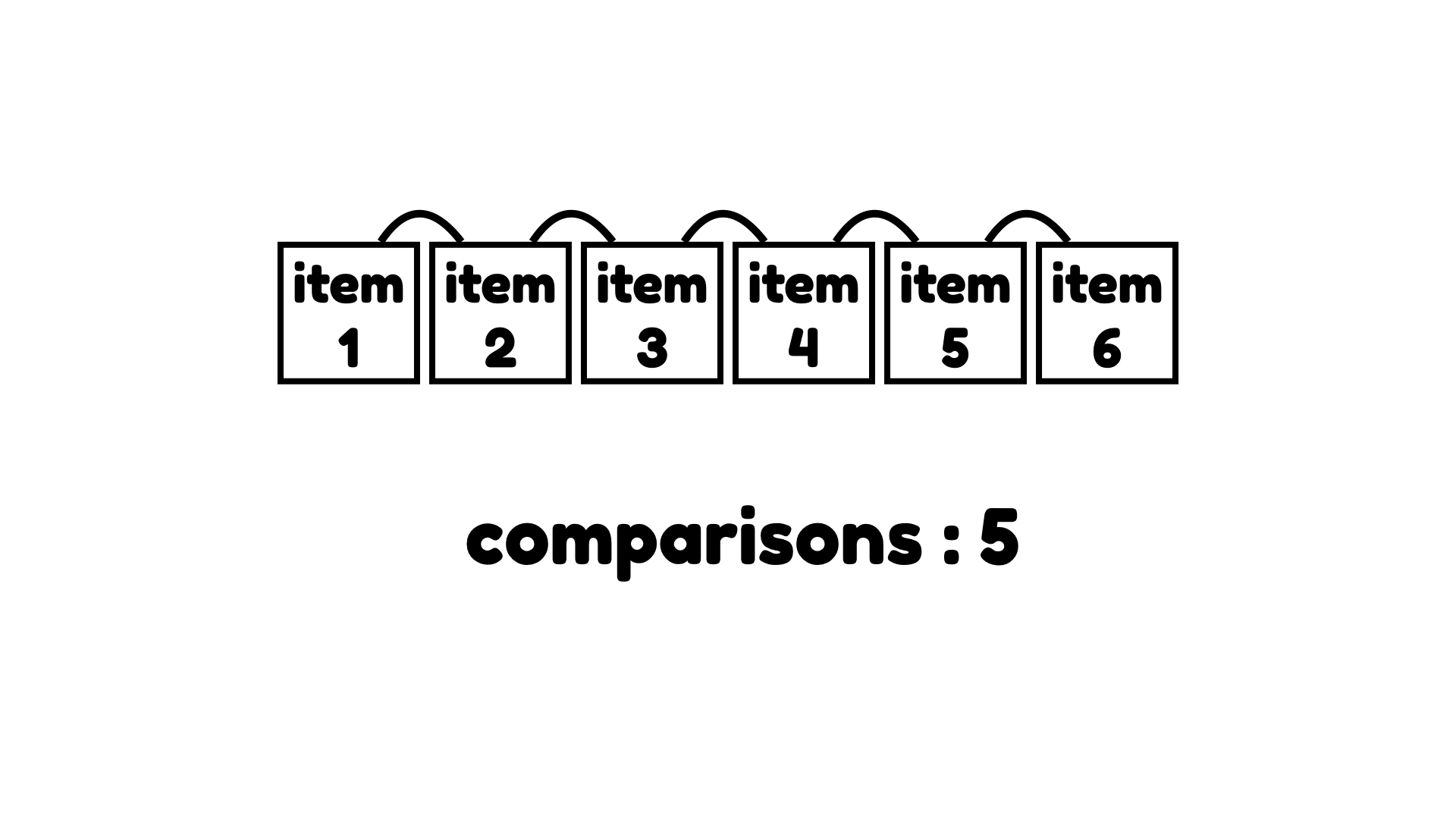
그렇다면 버블 정렬의 시간 복잡도는 어떨까? 배열의 N-1의 아이템을 비교해야 한다. 아이템이 6개면 5번 비교해야 하고, 다음 싸이클에서도 비교하고 반복이다.

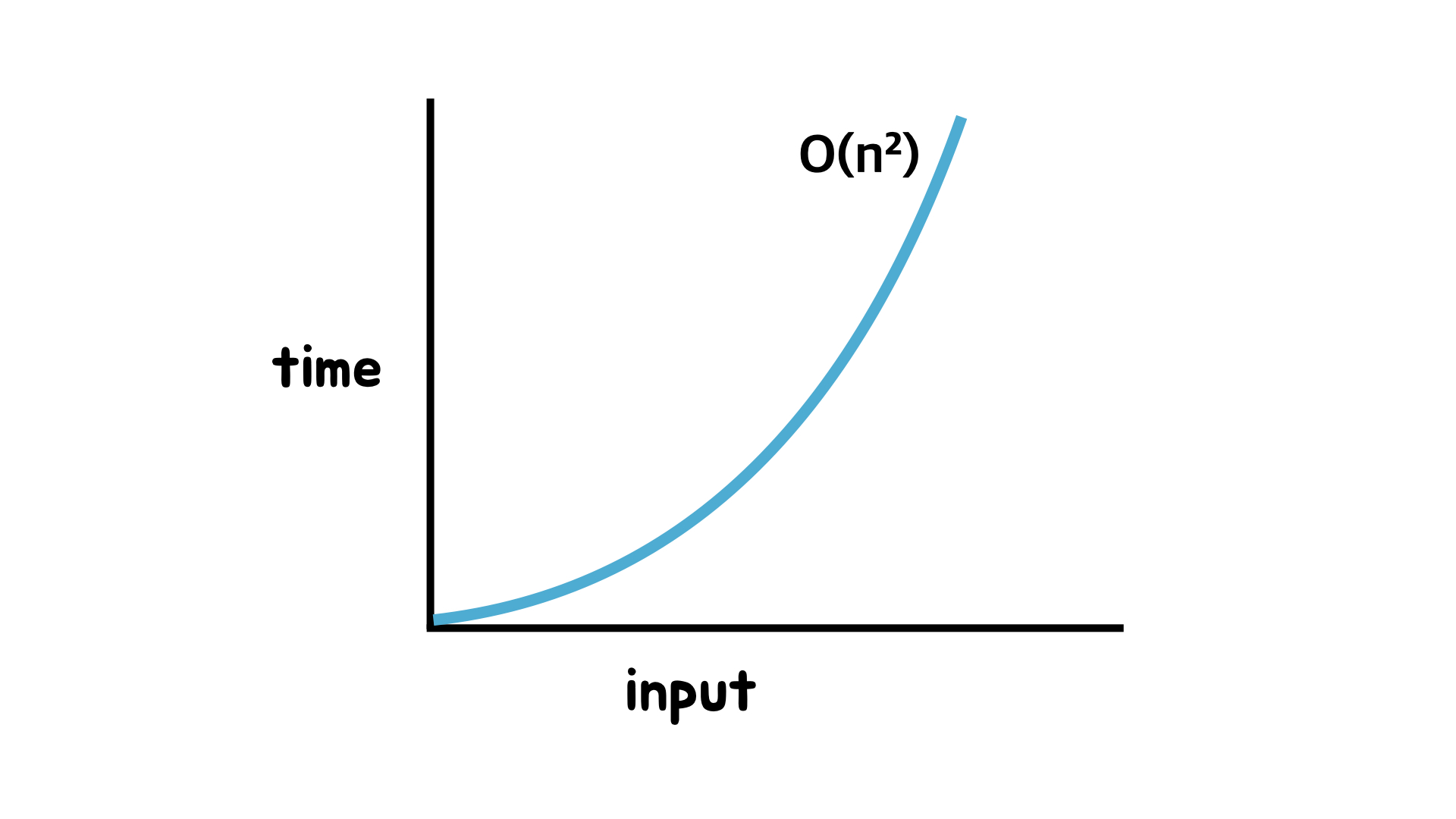
최악의 경우에는 모든 아이템을 교환해야 한다. 예를 들어, 작은 수에서 큰 수로 정렬하고 싶은데 배열이 큰 수에서 작은 수의 순으로 되어있는 경우이다. 따라서, 버블 정렬의 시간 복잡도는 O(n²)이다.

그리고 이건 그렇게 좋은 알고리즘이 아니다.

2. Selection Srot(선택 정렬)

아까 정렬한 동일한 배열로 작업해볼 것이다. 선택 정렬은 전체 아이템 중 가장 작은 아이템의 위치를 변수에 저장한다.

아래 배열에서 가장 작은 숫자는 5인데, 5보다 작은 숫자인 2가 있다.

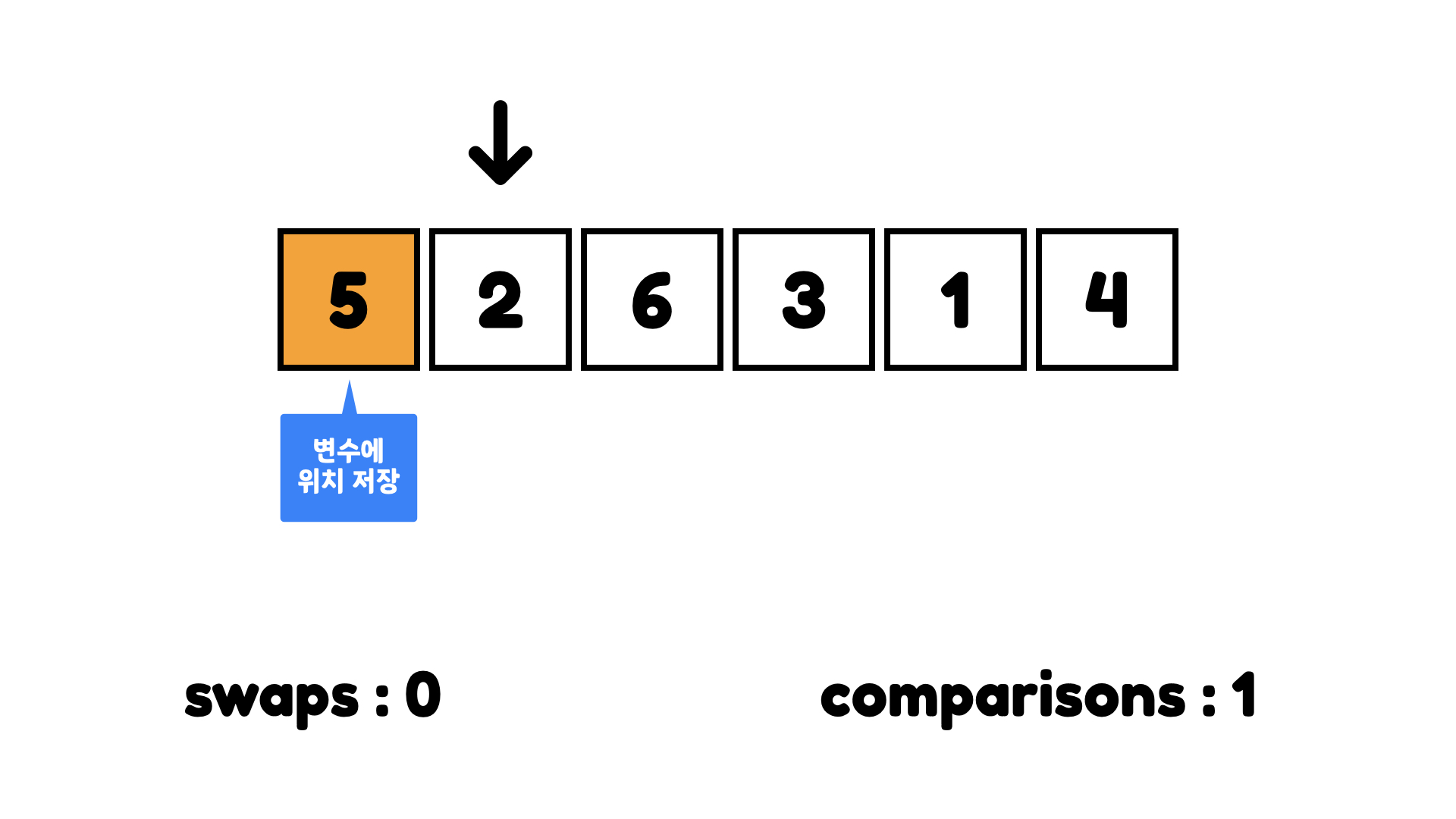
2의 위치를 변수에 저장하고 계속 체크하다가 1에 도착하면 해당 위치를 변수에 저장하고 싸이클을 끝낸다.

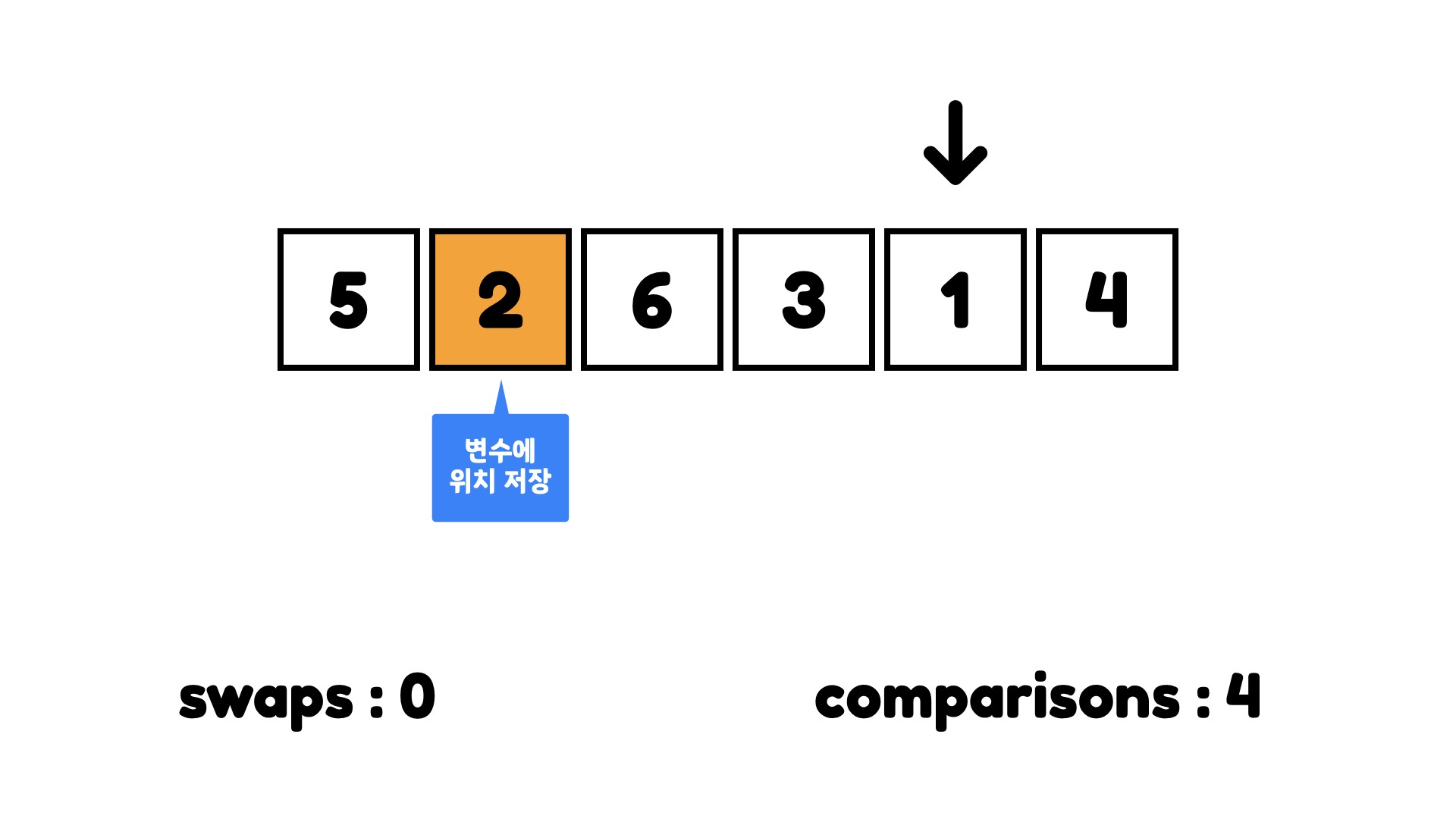
이렇게 배열에서 가장 작은 숫자가 어디에 있는지 알아냈다.

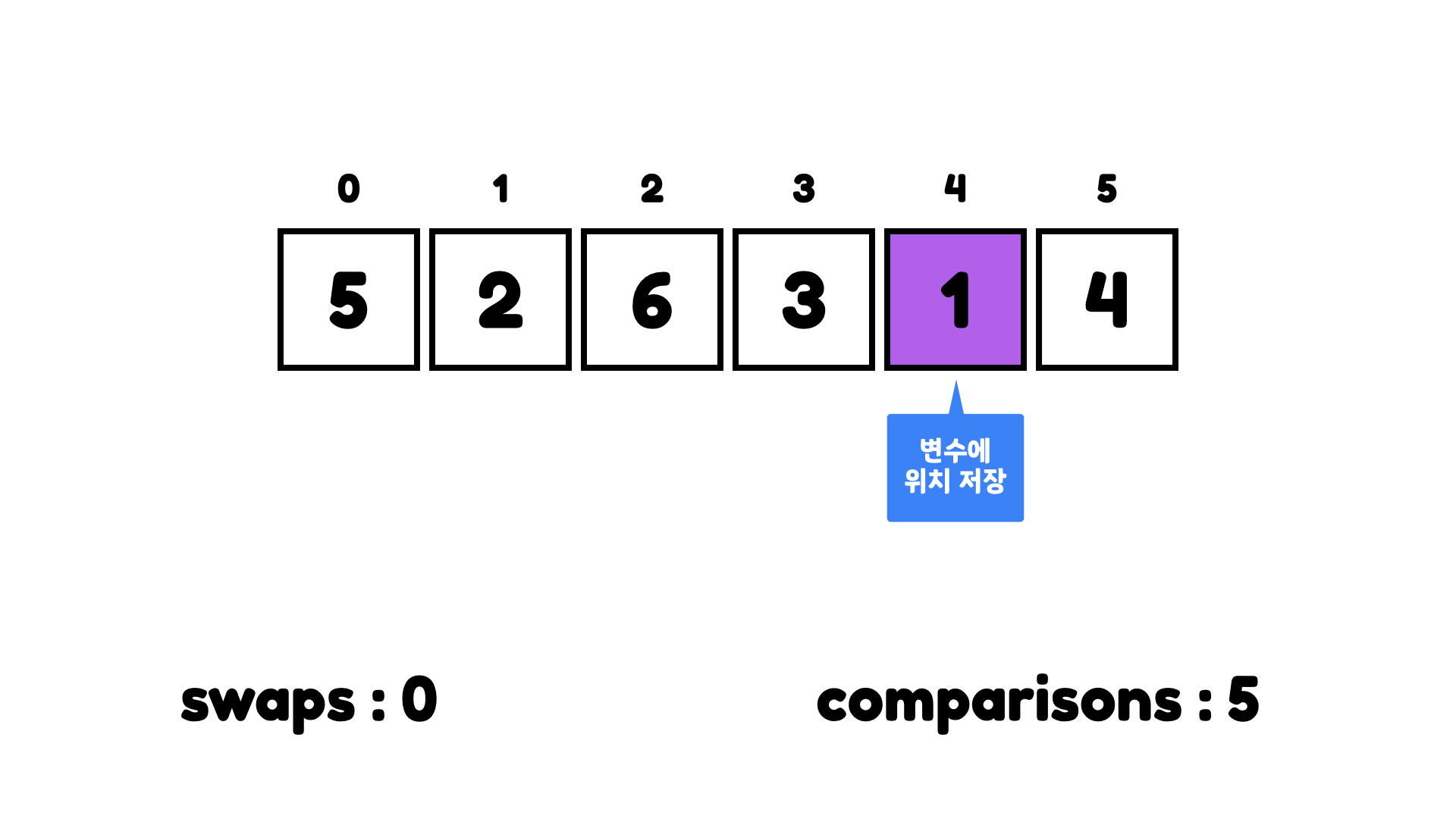
그럼 이제 가장 작은 숫자를 첫번째 아이템과 바꾼다.

그리고 다음 사이클을 시작할 때 두 번째 아이템부터 시작한다. 1은 이미 정렬했으니 정렬되지 않은 부분에서 가장 작은 숫자를 찾는다.

가장 작은 숫자 2를 찾고, 2는 이미 올바른 위치에 있으므로 교환하지 않는다.

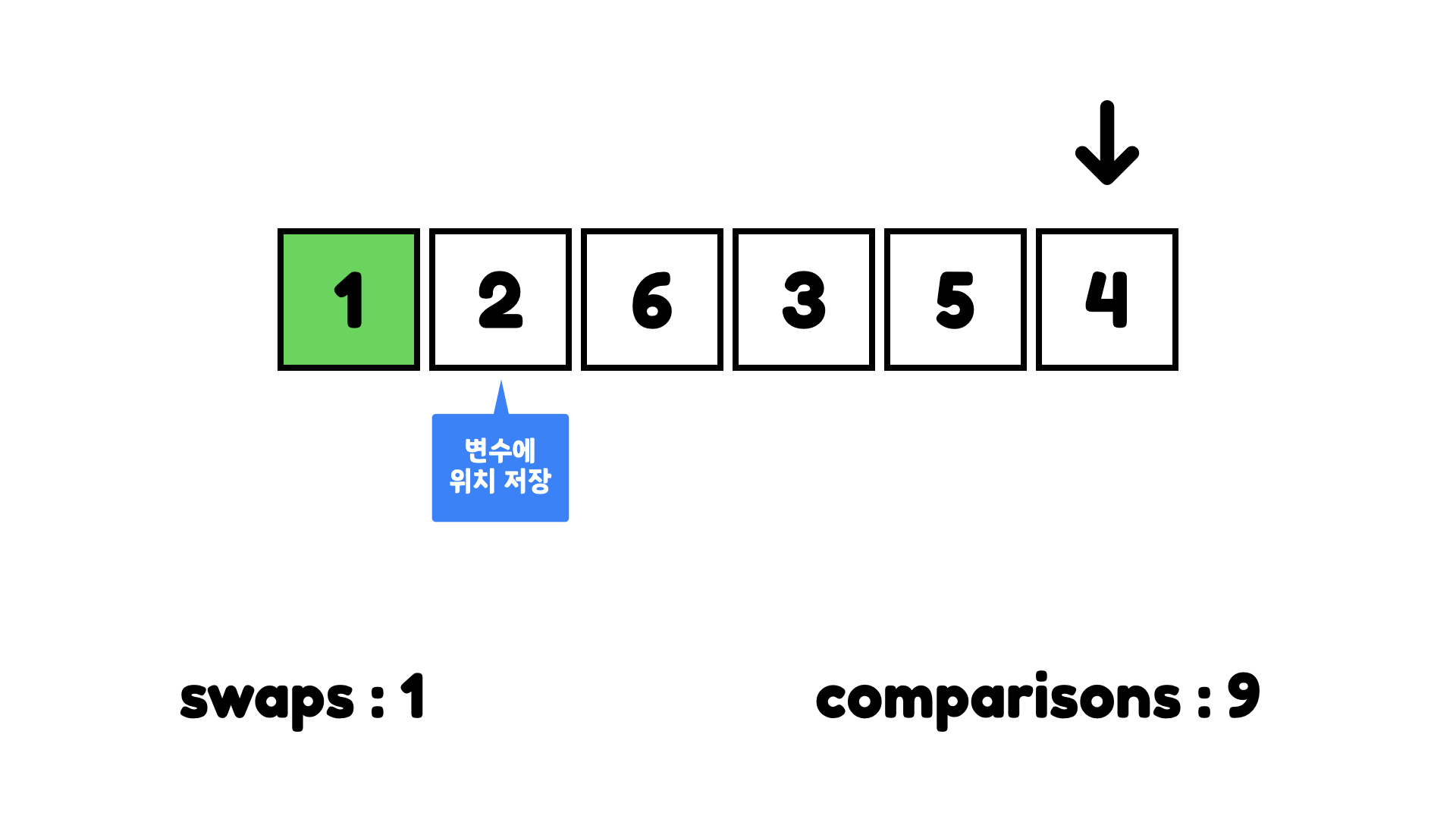
이 과정을 계속 반복한다.

선택 정렬의 시간 복잡도는 뭘까? 버블 정렬과 비슷하게 교환도 하고 비교도 한다. 또, 정렬되지 않은 배열에서 가장 작은 숫자를 찾으므로 N-1 비교를 하는 것이다. 이건 버블 정렬과 동일하다.

하지만 버블 정렬과 다르게 N 번의 교환을 하지 않는다. 선택 정렬에서는 매번 싸이클마다 한 번의 교환만 하면 된다. 즉, 선택 정렬은 버블 정렬보다 훨씬 낫다.

선택 정렬이 버블 정렬보다 2배 더 빠를 수도 있음에 불구하고 선택 정렬의 시간 복잡도 역시 O(n²)이다.

3. Insertion Sort(삽입 정렬)

앞에서 사용한 배열로 삽입 정렬을 해보면 인덱스 1번에서 시작한다.

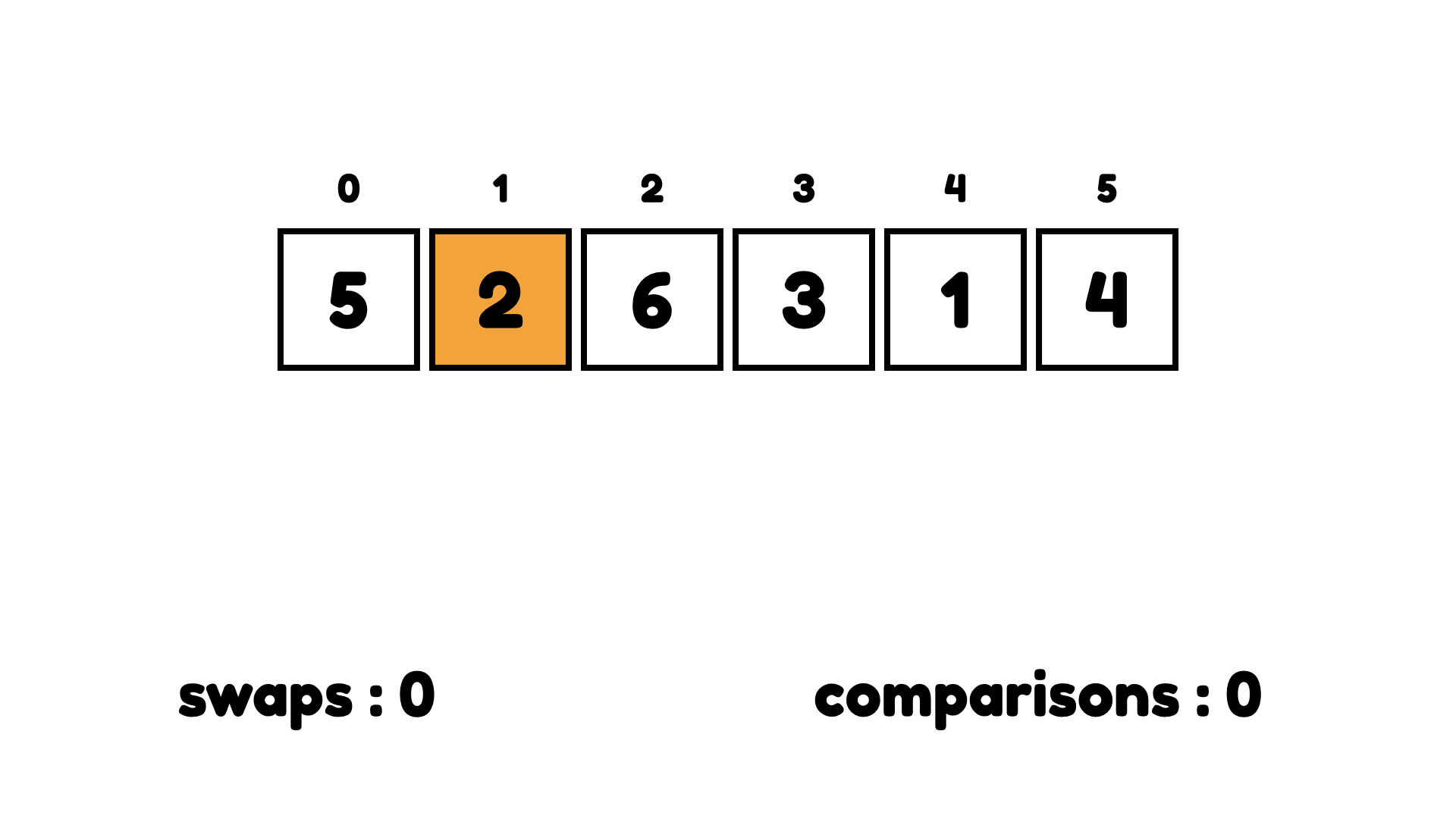
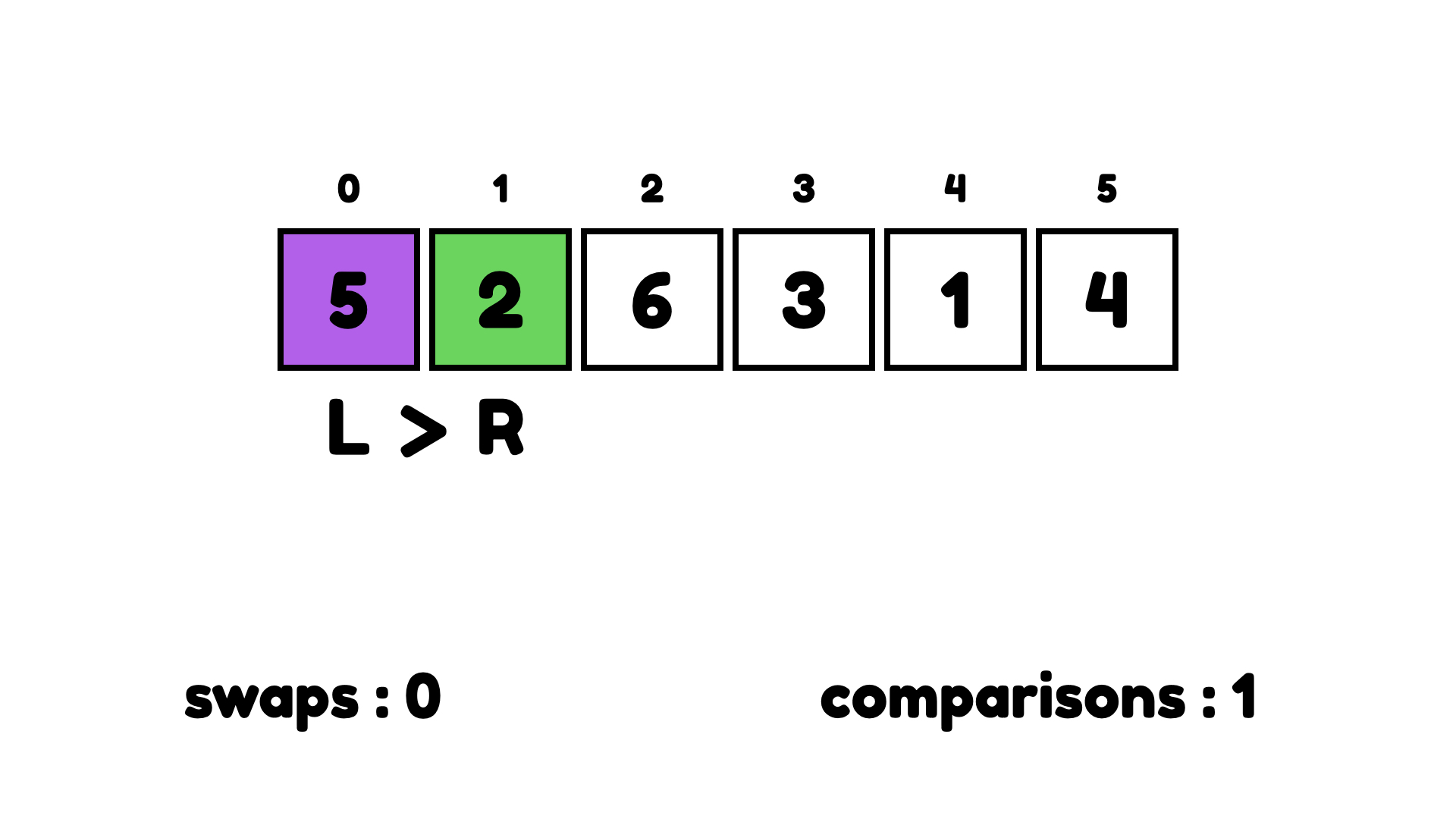
왼쪽에 2보다 큰 숫자가 있는지 살펴본다. 5가 2보다 크니까 교환한다.

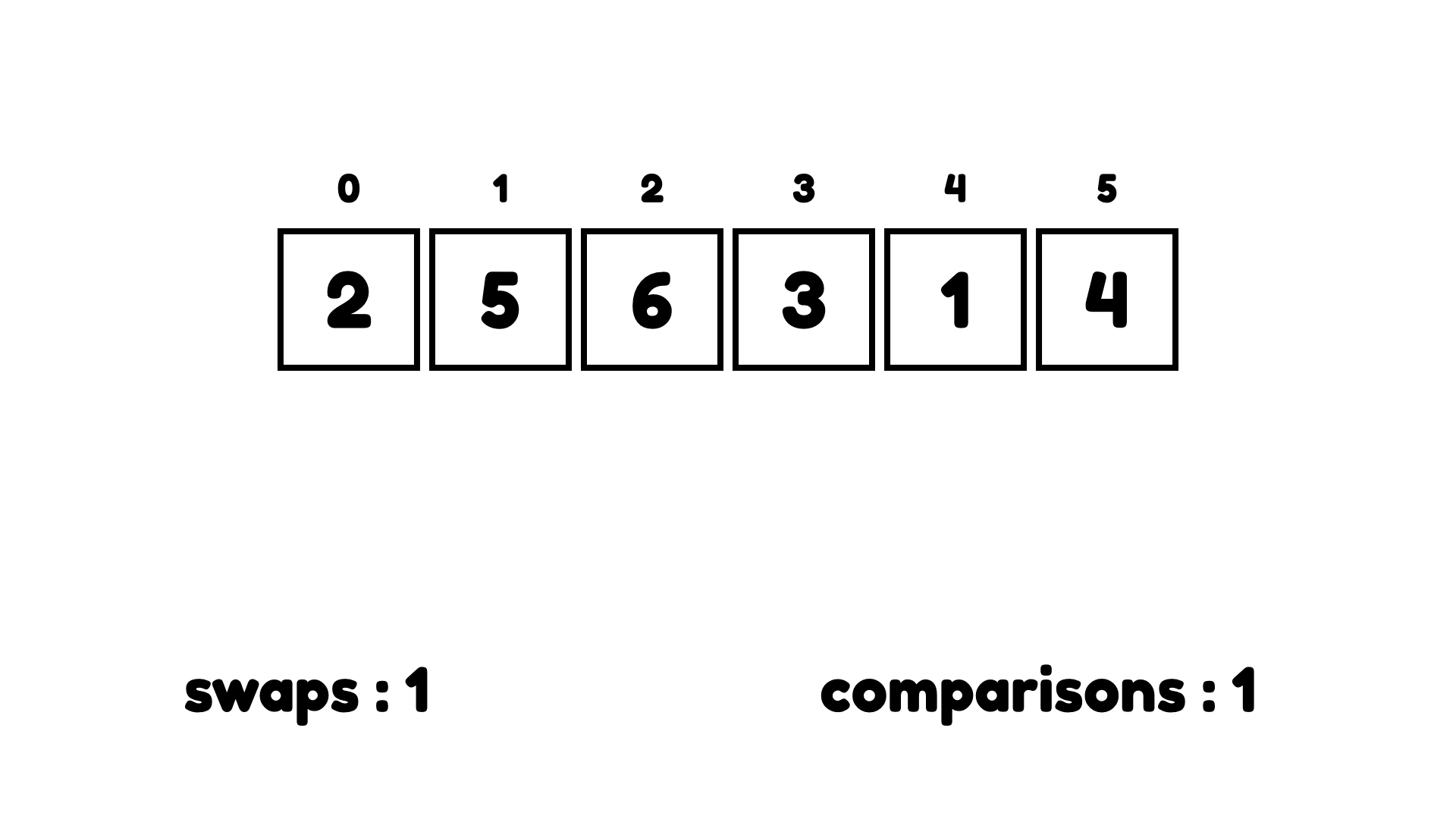
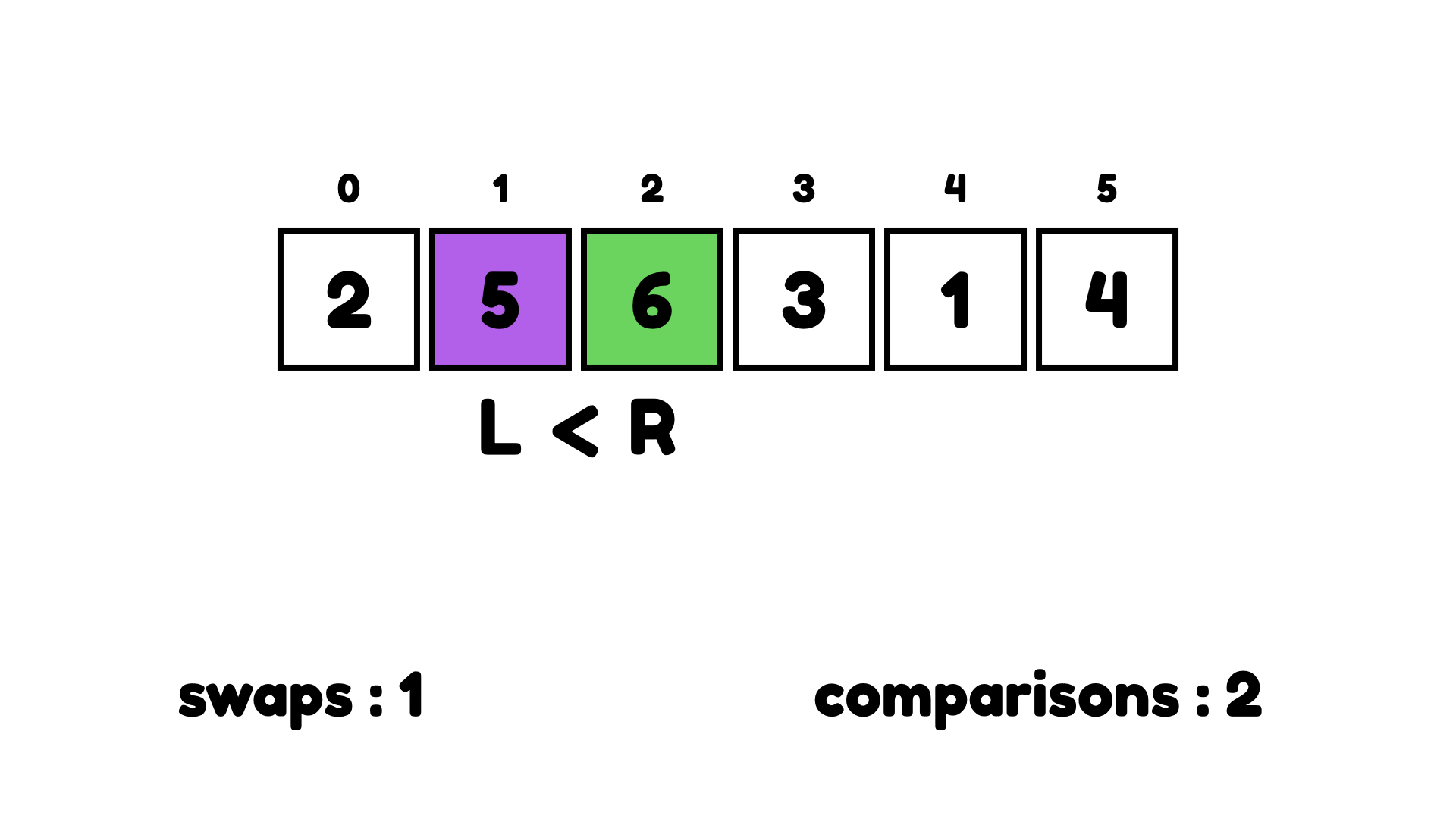
두 번째 싸이클은 6을 선택하고 왼쪽에 더 큰 숫자가 있는지 살펴본다. 없는 경우 계속 진행한다.

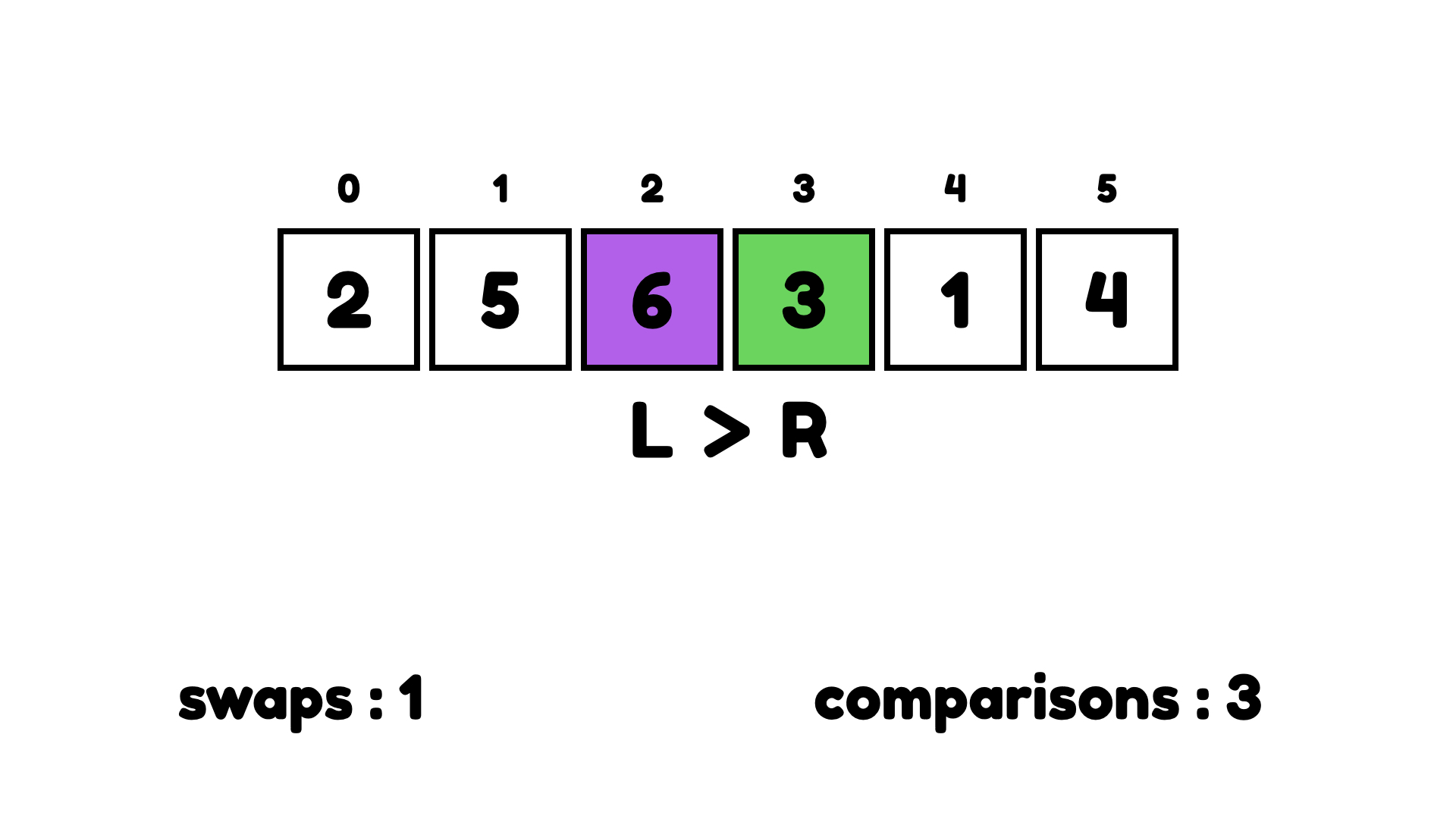
세번째 사이클에서 3을 선택하고 왼쪽에 더 큰 숫자가 있는지 확인한다. 6이 3보다 크니까 교환한다.

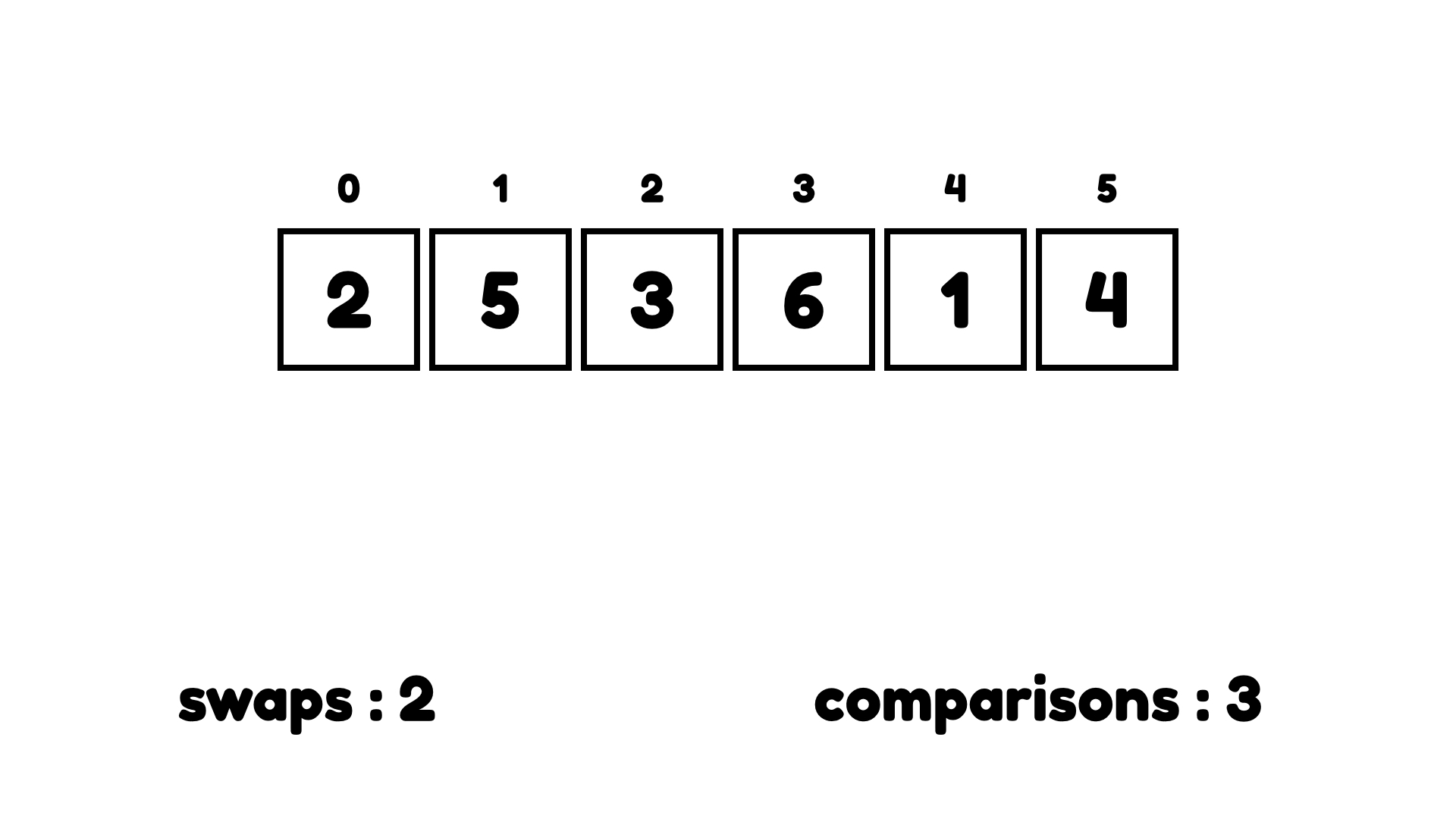
그리고 다시 3과 5를 비교한다. 5가 더 크니까 교환한다.

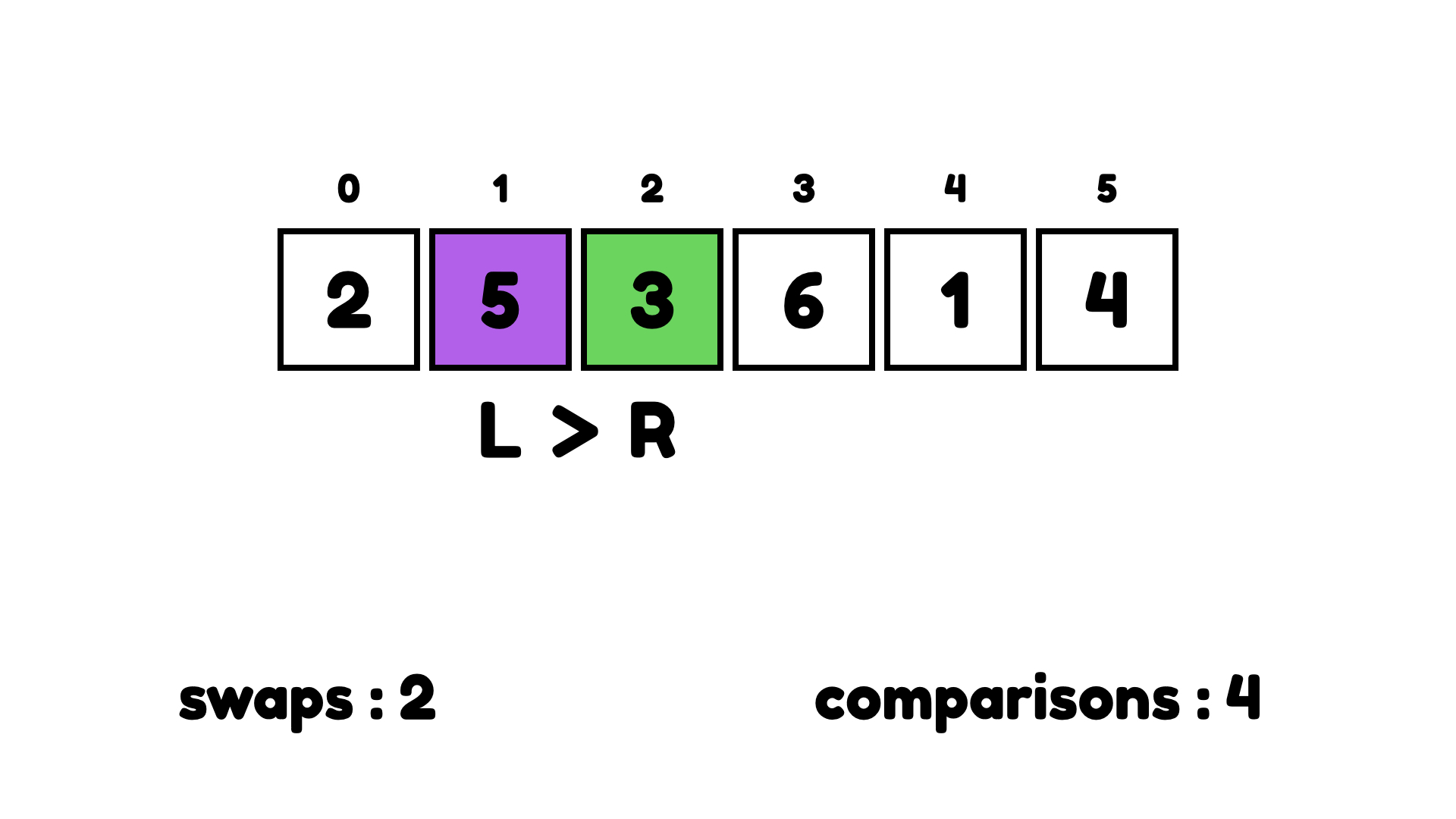
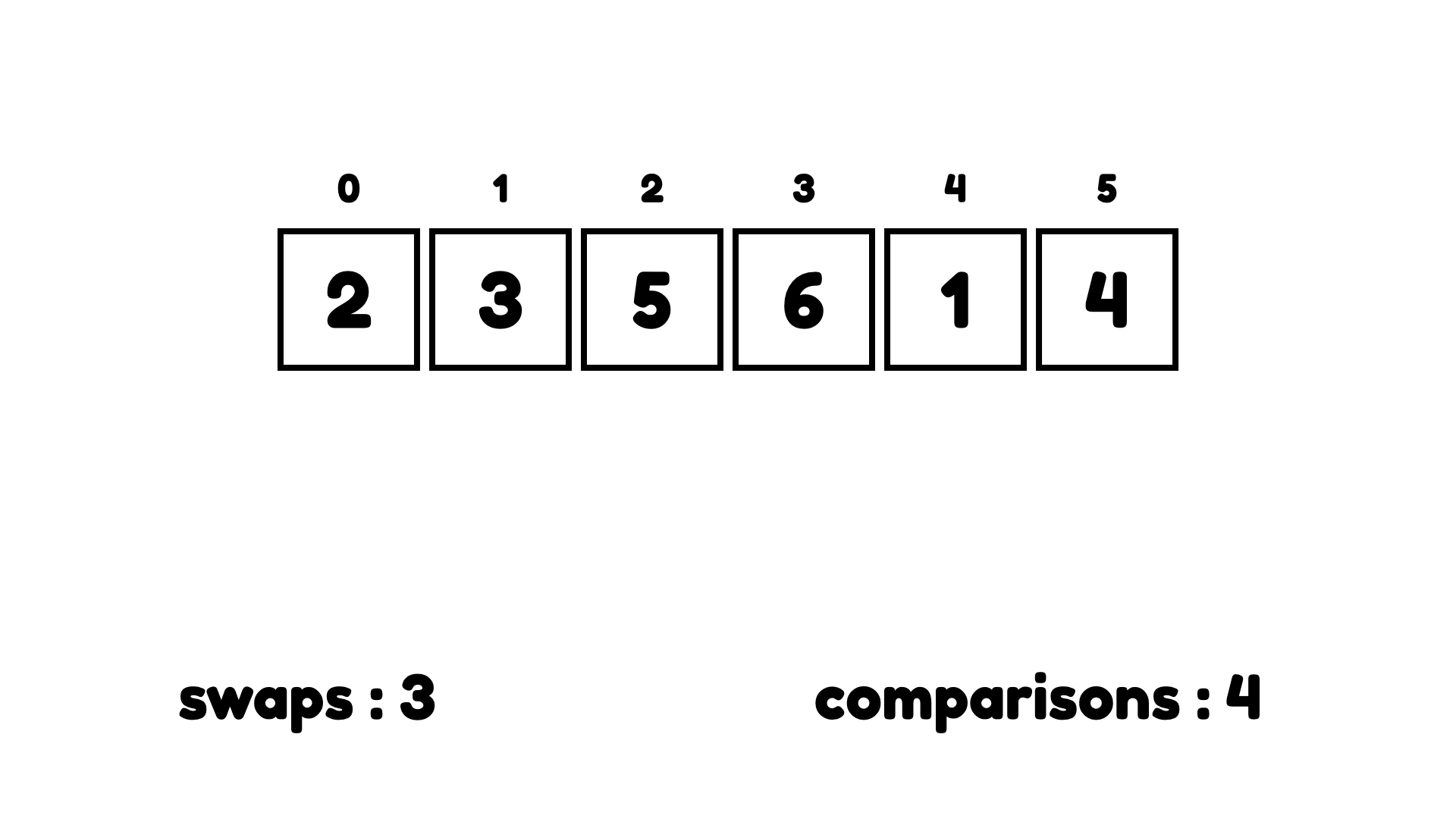
그리고 다시 3과 2를 비교하는데 2가 3보다 크지 않으니까 2는 올바른 위치에 있다고 말할 수 있다.

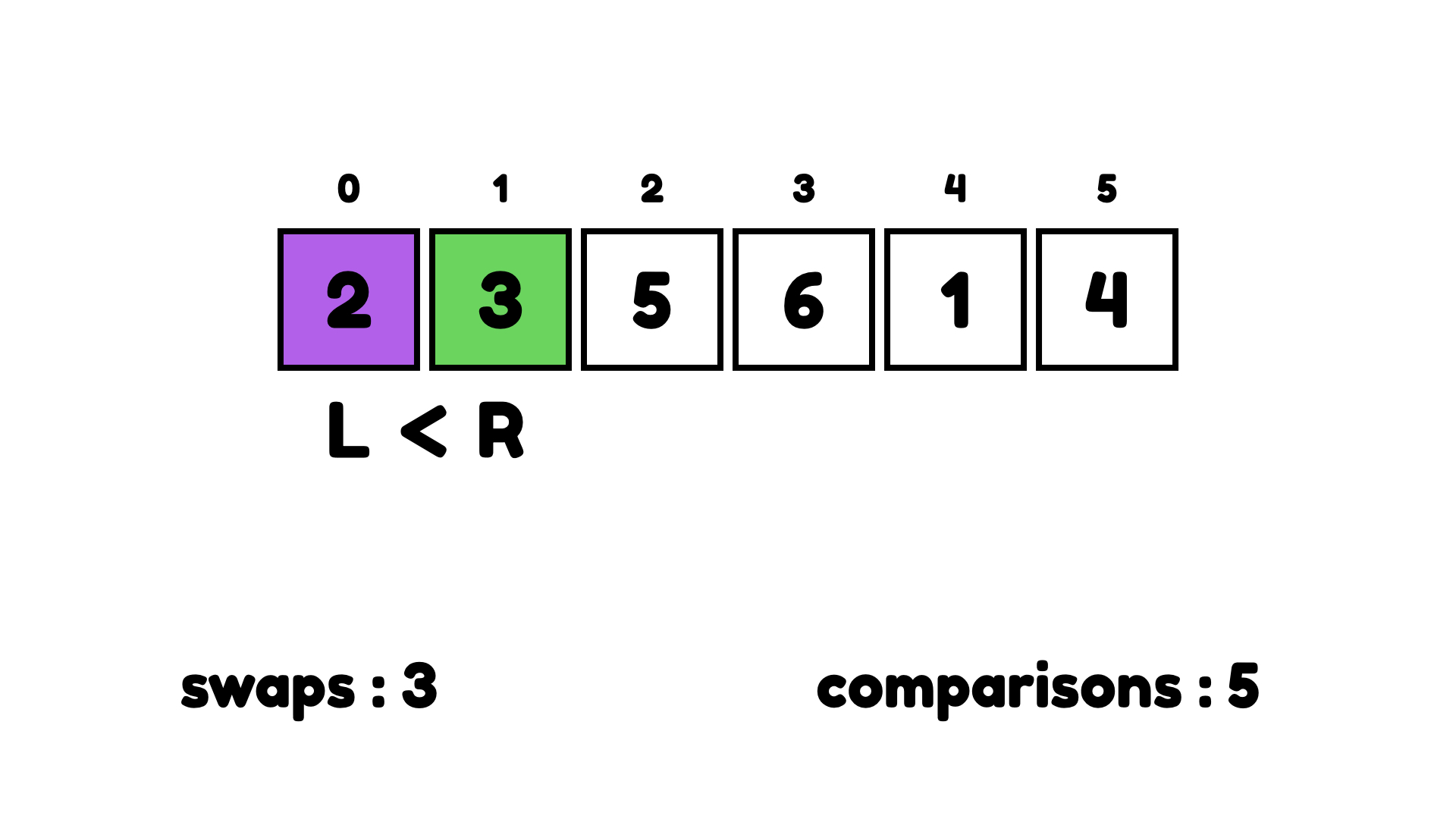
1과 4로 동일한 작업을 하면 끝난다. 삽입 정렬은 필요한 아이템만 스캔하고 선택 정렬은 전체 모든 아이템을 스캔하기 때문에 삽입 정렬은 선택 정렬보다 빠르다. 하지만, 삽입 정렬이 선택 정렬과 버블 정렬보다 빨라도 시간복잡도는 동일하게 O(n²)이다.

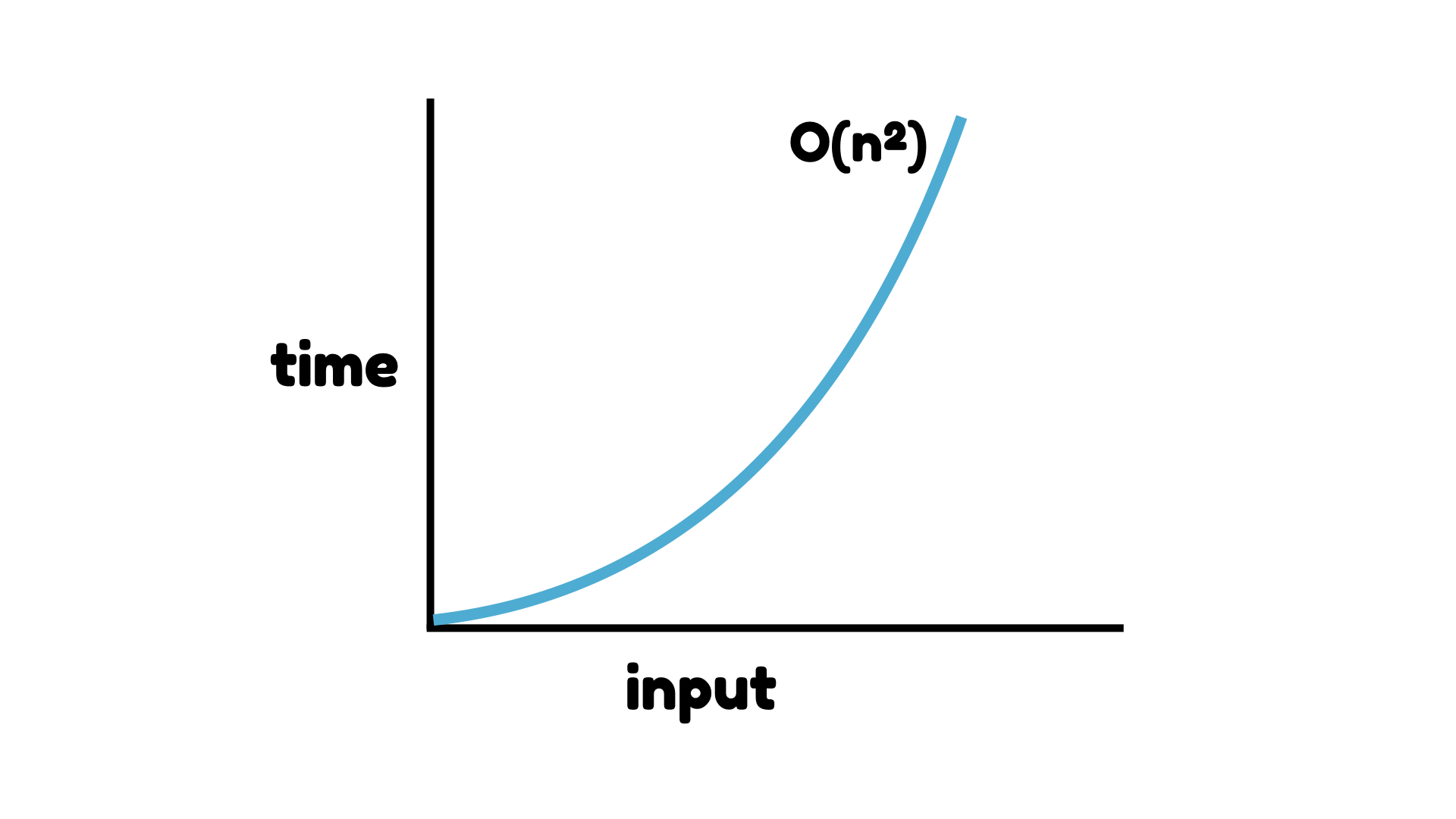
삽입 정렬 vs 선택 정렬

최악/최고의 케이스는 자주 발생하지 않고 대부분 평균적인 경우에 속하기 때문에 최악의 시나리오가 아닌 평균 시나리오를 봐야한다.

그걸 감안하고 알고리즘들을 살펴보면 삽입 정렬, 선택 정렬 둘 다 평균적으로 최악의 경우 이차 시간복잡도를 가지고 있다. 그러나 삽입 정렬의 경우 O(n)이 최고의 시나리오에서 발생한다.

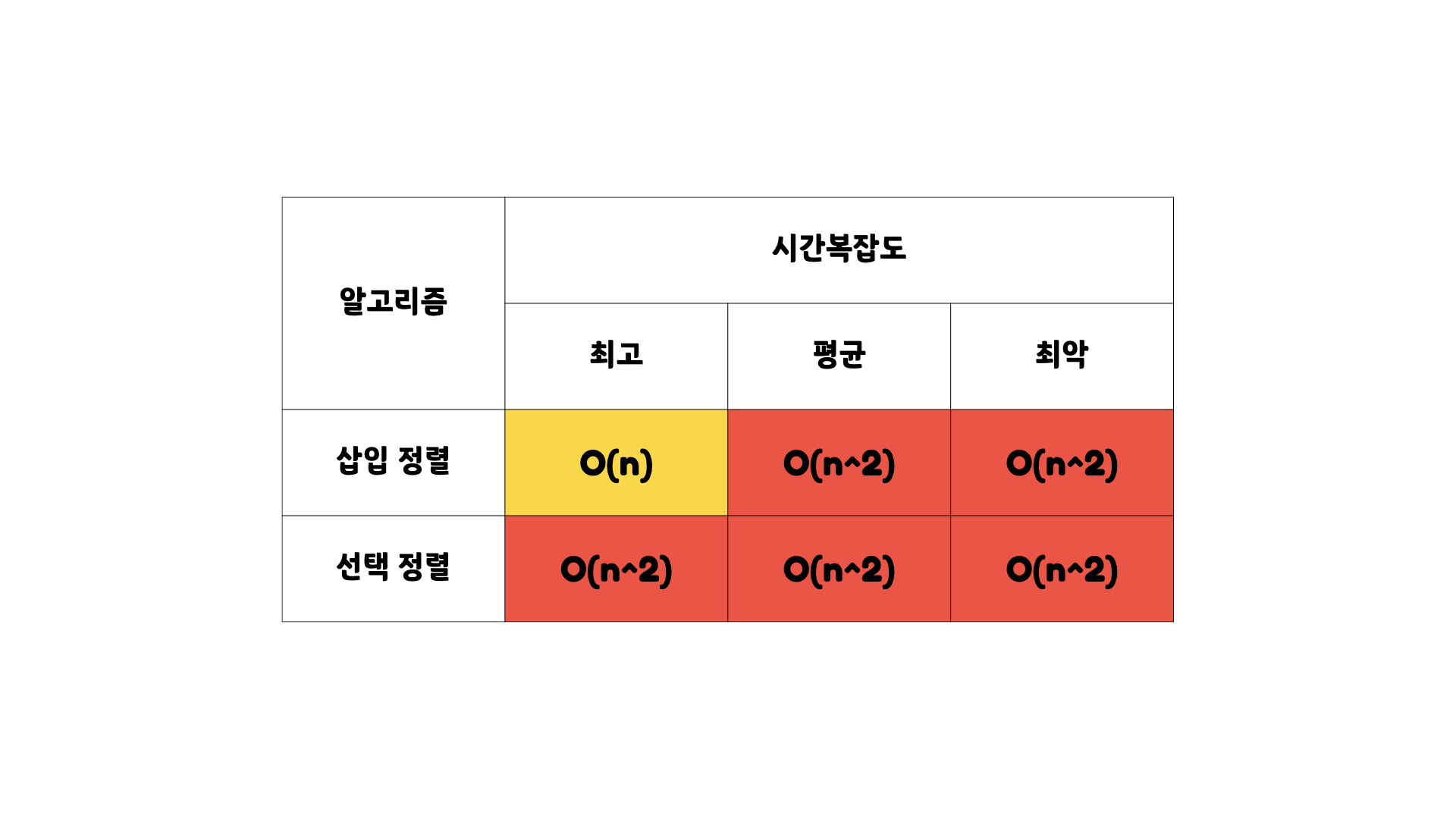
O(n)은 이차 시간복잡도와 비교해서 최고의 알고리즘이다.

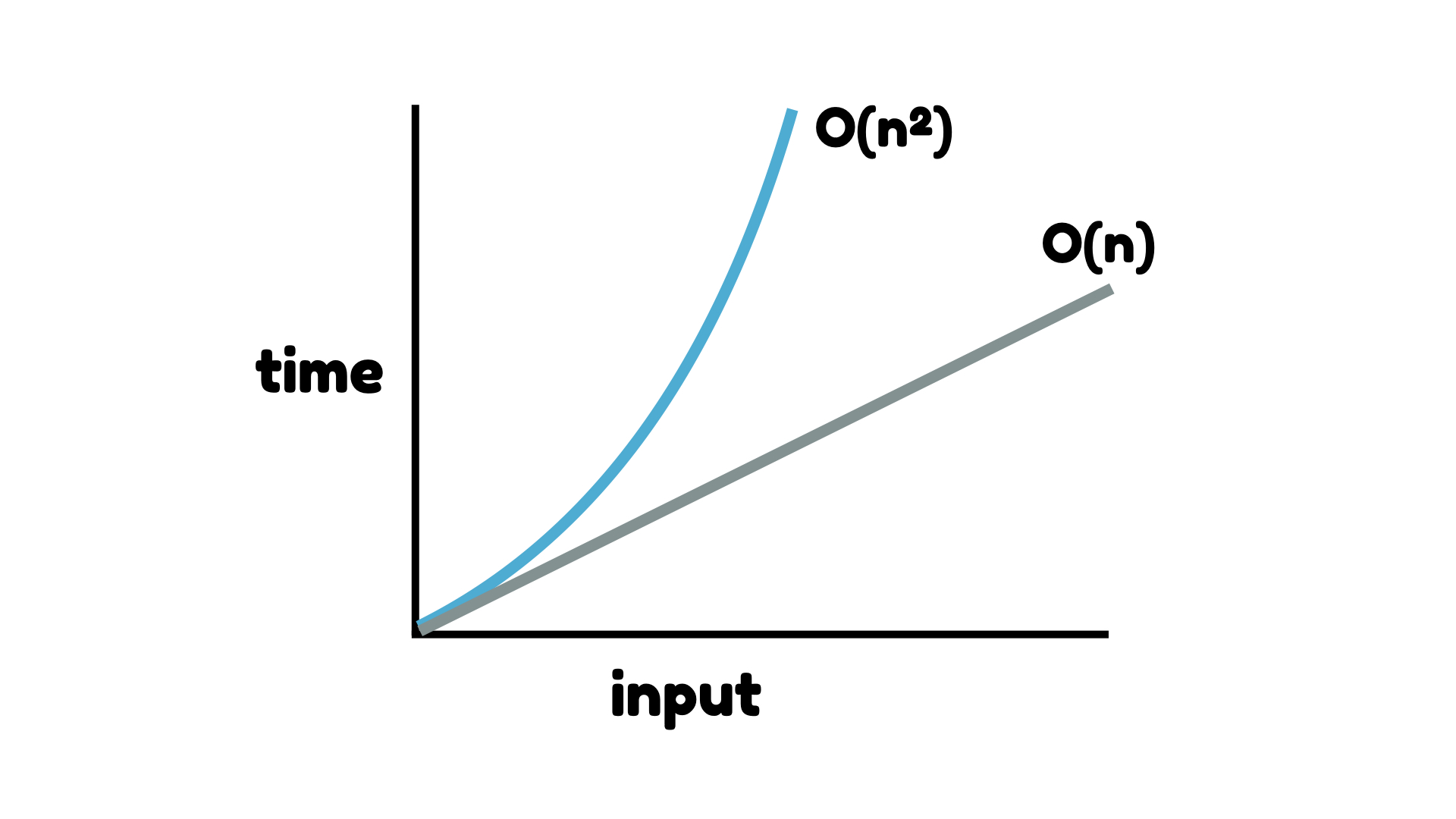
이렇게 동일한 시간복잡도를 갖고있다 하더라도 매우매우 다르게 나타날 수 있다. 삽입, 선택 정렬은 작은 DB 기준으로는 훌륭한 알고리즘이다. 물론, 데이터가 커지면 커질수록 좀 느려지겠지만 그때 다른 걸 살펴봐야할 것이다.

---

Sorting은 정말 많은 개발자들이 관심을 갖는 주제고, 다들 한 번은 정렬을해 봤을 것이다. 그만큼 정말 중요하기 때문에 잘 알아둬야 한다.

버블 정렬은 잘 사용되지 않기 때문에 어떻게 해야 하는지까지 정확히 암기할 필요는 없지만 정렬이 뭔지, 정렬이 왜 복잡한지, 더 좋은 솔루션이 왜 필요한지를 이해할 수 있다.

• 버블 정렬
  • 인접한 원소끼리 비교하여 교환하는 방식
  • 셋 중에 제일 느리지만 단순함
• 선택 정렬
  • 최솟값을 찾아서 맨 앞으로 이동하는 방식
  • 버블 정렬보다 좋음
• 삽입 정렬
  • 앞에서부터 차례대로 이미 정렬된 부분과 비교하여 교환하는 방식
  • 셋 중에 제일 빠르지만 배열이 길어질수록 효율성이 떨어짐

모두 시간 복잡도는 O(n²)
선택 정렬과 삽입 정렬은 사용할 메모리가 제한적인 경우에 사용하면 좋음

💙 참고한 영상 💙

https://youtu.be/Bor_CRWEIXo