문제

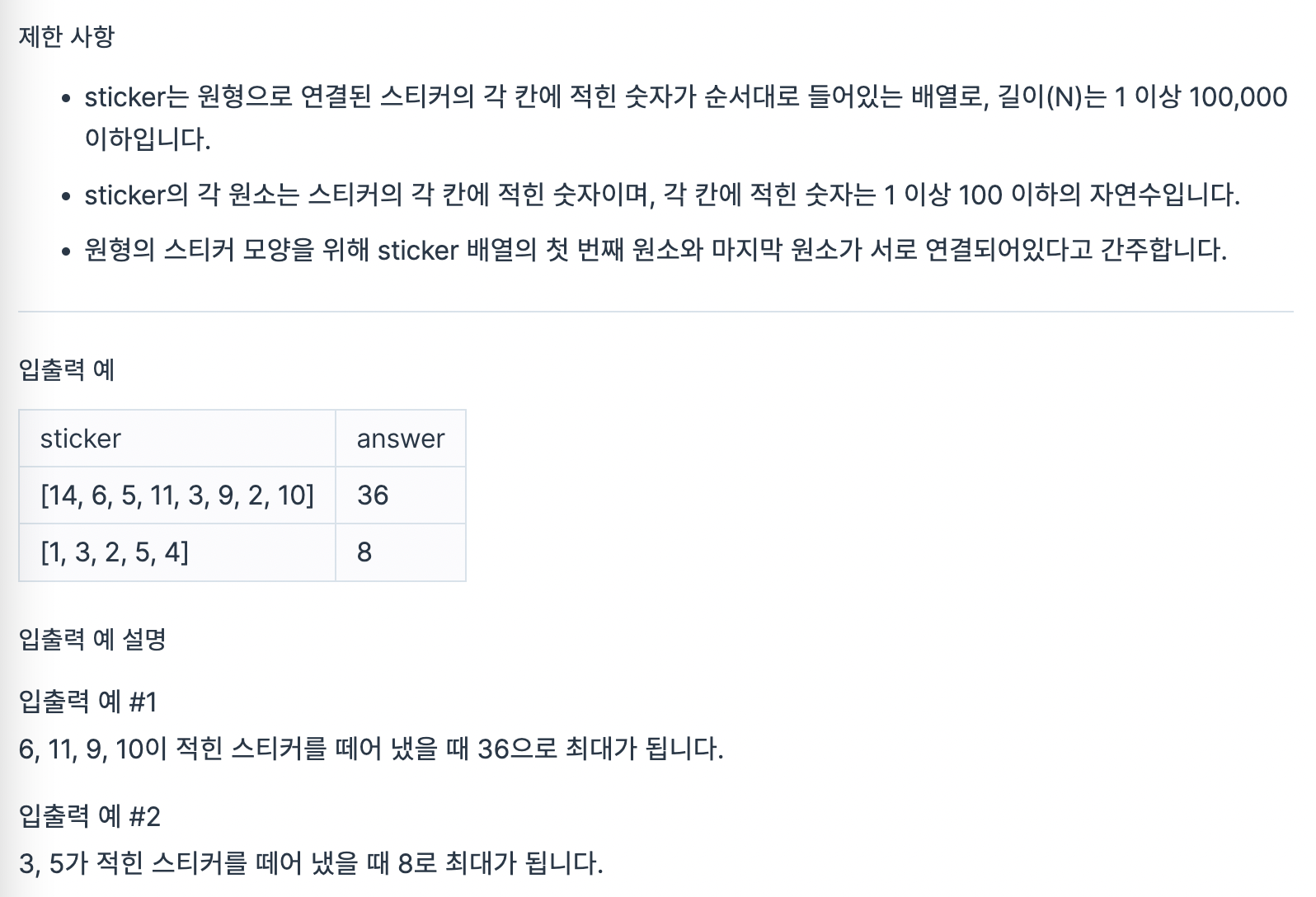
풀지 못한 이유
- 힙이나 DFS/BFS는 아닌 것 같아서 아무래도 DP 같았다. DP는 점화식을 세워야 하는데 도무지 생각이 나질 않았다.
- 혼자 풀어야 실력이 늘 테지만 질문하기에 있는 힌트를 보고 말았다. 이렇게라도 다시 한번 곱씹어 보려고 한다.
풀이) DP
다이나믹 프로그래밍(동적 계획법)은 중복되는 연산을 줄일 수 있는 기법으로 크게 탑다운과 보텀업 방식이 있다. 재귀 함수를 이용하면 탑다운 방식이라 하고, 반복문을 이용하면 보텀업 방식이라 한다. 재귀 함수의 스택 크기가 한정되어 있을 수 있기 때문에 탑다운보단 보텀업을 권장한다.
🍯 문제가 다이나믹 프로그래밍 유형임을 파악하는 방법
1. 완전 탐색 알고리즘으로 접근했을 때 시간이 매우 오래 걸리는가?
2. 그렇다면 다이나믹 프로그래밍을 적용할 수 있는가?
3. 중복하는 부분이 있는가?
def solution(sticker):
# 리스트에 원소가 한 개면 아래 코드를 진행할 수 없다.
if len(sticker) == 1:
return sticker[0]
# 처음과 마지막은 연결되어 있다고 했으니, 처음 원소를 제외했을 때와 마지막 원소를 제외했을 때로 나눈다.
a = sticker[1:]
b = sticker[:-1]
i = 1
while i < len(sticker)-1:
# 인덱스가 1이면 앞 원소와 현재 원소 비교
if i == 1:
a[i] = max(a[i-1], a[i])
b[i] = max(b[i-1], b[i])
# 인덱스가 2이상이면 앞 원소와 여태까지 합에 현재 원소를 더한 값 비교
else:
a[i] = max(a[i-1], a[i-2]+a[i])
b[i] = max(b[i-1], b[i-2]+b[i])
i += 1
# 최종적으로 두 리스트의 마지막 원소가 최대합이기 때문에 둘 중 더 큰 값을 리턴
return max(a[-1], b[-1])문제에서 첫 번째 원소와 마지막 원소는 이어져있다고 본다고 했으므로, 첫 번째 원소를 제외했을 때와 마지막 원소를 제외했을 때로 나눠야 한다.
예시) [14, 6, 5, 11, 3, 9, 2, 10]
-> [6, 5, 11, 3, 9, 2, 10] | [14, 6, 5, 11, 3, 9, 2] 그리고 각 리스트의 두 번째 원소부터 마지막까지 반복할 건데, 그 이유는 앞에 원소와 비교하기 위해서 첫 번째 원소는 건너띄는 셈이다. 이때 중요한 게 두 번째 원소(index=1)는 앞에 첫 번째 원소밖에 없기 때문에 두 원소만 비교한다. 그리고 세 번째 원소(index=2)부터는 전전 원소와 여태까지 구한 합(전 원소)에 자신을 더한 값을 비교한다.
예시) [6, 5, 11, 3, 9, 2, 10]
i=1: [6, 6, 11, 3, 9, 2, 10]
i=2: [6, 6, 17, 3, 9, 2, 10]
i=3: [6, 6, 17, 17, 9, 2, 10]
i=4: [6, 6, 17, 17, 26, 2, 10]
i=5: [6, 6, 17, 17, 26, 26, 10]
i=6: [6, 6, 17, 17, 26, 26, 36]그럼 제일 마지막 원소가 이 리스트에서의 최대합인 것이다. 처음에 두 리스트로 나눴으니 각각의 마지막 원소를 비교해서 더 큰 값을 리턴한다.
return max(a[-1], b[-1])풀이 회고
DP 문제는 중복되는 부분을 캐치하는 게 정말 중요한 것 같다. 이번 문제의 핵심은 스티커를 떼면 양쪽은 앞으로 사용할 수 없다는 것이다. 그리고 어떻게 비교해야 할 지도 잘 생각해야겠다. 현재 스티커가 a[i] 이면 a[i+2]부터 마지막까지는 그다음 뗄 수 있는 후보인 셈이다. 그중에서 어떻게 떼야 제일 최대합을 도출할 수 있을지가 포인트였다.

