[인공지능] 맹목적 탐색(Blind Search) 기법 비교

탐색을 할 때에는 어떤 노드를 먼저 탐색하느냐가 포인트가 된다고 한다
탐색 기준에 따라 여러 탐색 기법이 존재하는데
그 중 가장 간단한 맹목적 탐색 기법에 대해 정리해보려 한다!

1. 깊이 우선 탐색 (DFS)

- 발견과 동시에 탐색의 대상이 된다
- OPEN의 자료구조가 Stack이 되어야 한다 (나중에 들어간 후계노드가 먼저 탐색되어야 하므로)
- 확장한 노드 수와 방문한 노드 수를 적기는 했지만 이 경우 목표 상태가 없어서 큰 의미는 없다
- 장점: 발견과 동시에 탐색하기 때문에 메모리 공간 사용 효율이 좋다
- 단점: 그냥 가장 먼저 찾은 목표노드에 대한 경로를 반환하기 때문에 최적해를 보장해주지 않는다

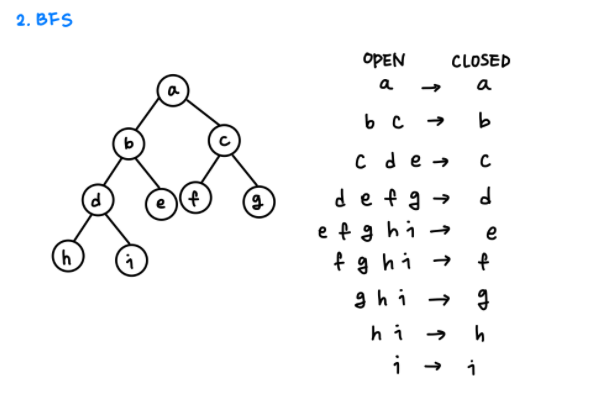
2. 너비 우선 탐색 (BFS)

- 같은 depth에 있는 노드들을 우선적으로 탐색한다
- OPEN의 자료구조가 Queue가 되어야 한다 (후계노드들은 부모노드보다 depth가 높으므로 부모노드 이후에 탐색되상이 된다)
- 장점: depth가 낮은 노드가 우선적으로 탐색되기 때문에 최적해를 보장해준다
- 단점: 메모리 공간 사용이 비효율적이다 (아마 BFS보다 더 많은 노드를 저장해두어야 해서 그런 것 같다)

3. 반복적 깊이 심화 탐색 (iterative-deepening search)

- DFS와 BFS의 장점만을 갖춘 방법으로 맹목적 탐색 기법 사용 시 우선적으로 고려되는 방법이다
- Depth 제한이 처음부터 정해져있는 DFS와 다르게, Depth를 하나씩 확장하며 반복적으로 깊이 우선 탐색을 진행한다
- 탐색 방식 자체는 DFS와 같아서 메모리 효율이 좋고, Depth를 하나씩 확장하기 때문에 최적해도 보장해준다

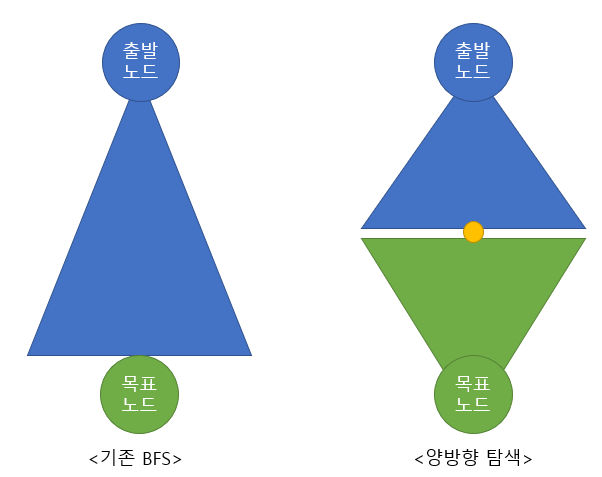
4. 양방향 탐색(Bidirectional search)

- 최적해를 보장해준다
- BFS 대비 메모리 효율이 좋고 더 빠르다
- BFS는 모든 branch factor에 대해 탐색해야 해서 깊이 보기에는 어렵고 시간이 오래걸리는데 그러한 단점을 보완해주는 것 같다

5. 균일 비용 탐색 (Uniform cost search)

- 비용이 있는 문제에서의 맹목적 탐색 기법이다
- 시작노드부터 현재노드까지 사용된 경로비용을 기준으로 더 낮은 비용이 드는 쪽으로 탐색한다

- 새로운 노드를 발견하면 다음과 같은 일들을 수행한다
1) 새로운 노드와 같은 노드가 OPEN에 있다면,
- 새로운 노드의 비용이 더 적을 경우 OPEN에 있는 노드를 새로운 노드로 대체
- 새로운 노드의 비용이 더 클 경우 새로운 노드를 무시하고 OPEN에 있는 노드를 유지
2) 새로운 노드와 같은 노드가 CLOSED에 있다면,
- CLOSED에 있는 노드의 비용이 적을 수 밖에 없으므로 새로운 노드를 무시
(CLOSED에 있는 노드는 먼저 발견되어서 추가적 비용이 더해지지 않기 때문에 새 노드보다 비용이 적다)
3) 새로운 노드와 같은 노드가 OPEN과 CLOSED에 없다면 그냥 OPEN에 추가한다
- 마지막으로 OPEN에 있는 노드를 전부 오름차순 정렬한다

• 경로 비용 계산식

g(new node)     = g(parent node) + C(new node, parent node)
새로운 노드의 비용 = 부모노드의 비용  + 새로운 노드와 부모 노드 사이의 비용