NP-완전 문제

민정·2022년 6월 7일
algorithm
0

알고리즘 이론 정리

목록 보기
6/6

다항식 시간보다 큰 복잡도를 가진 알고리즘으로 해결되는 문제의 집합 중에서,
지수 시간 복잡도를 가진 알고리즘으로 해결되는 문제들을 NP-완전 문제라고 한다.

NP-완전 문제는 아래의 특성을 가진다 :

  • 어느 하나의 NP-완전 문제에 대해서 다항식 시간에 해를 찾을 수 있는 알고리즘을 찾아내면,
    모든 다른 NP-완전 문제도 다항식 시간에 해를 찾을 수 있다는 특성을 가진다.
    : 문제 B를 해결하는 알고리즘에 대해서 다항식 시간에 해를 찾을 수 있는 알고리즘을 찾았다고 가정하자. 그러면 문제 A를 해결하기 위해 문제 B를 해결하는 알고리즘을 사용할 수 있으므로, 문제 A도 다항식 시간에 해를 찾을 수 있다.
    이러한 [ 문제의 변환 과정 ]은 다음과 같다:
    (1) 문제 A의 입력을 문제 B의 입력 format과 일치하게 변환한다.
    (2) 변환된 입력으로 문제 B를 해결하는 알고리즘을 수행한다.
    (3) 수행 결과인 해를 문제 A의 해로 변환한다.
  • 주어진 입력에 대해서 하나의 해를 추측하고, 추측한 해를 다항식 시간에 확인하여 yes 혹은 no로 답한다.

yes 혹은 no로 답하는 유형의 문제를 결정 문제라고 한다.
(ex. 각 도시를 1번씩만 방문하고, 시작 도시로 돌아오는 경로의 거리가 K보다 짧은 경로가 있는가?:
여행자 문제[TSP]: 최단 경로의 거리를 찾는 문제에서 상수 K를 사용하는 결정 문제로 변형)

근사 알고리즘

최적해에 근사한 해를 찾는 알고리즘을 말한다.
근사 알고리즘은 근사해를 찾는 대신에 다항식 시간의 복잡도를 가진다.
근사 알고리즘은 근사해가 얼마나 최적해에 가까운지를 나타내는 근사 비율을 알고리즘과 함께 제시하여야 하며, 근사 비율이 1.0에 가까울수록 정확도가 높다.
최적해를 구할 수 없으므로, 최적해를 대신할 수 있는 '간접적인' 최적해를 찾고, 이를 최적해로 삼아서 근사 비율을 계산한다.

(1) 여행자 문제

여행자가 임의의 한 도시에서 출발하여 다른 모든 도시를 1번씩만 방문하고, 다시 출발했던 도시로 돌아오는 여행 경로의 길이를 최소화하는 문제

알고리즘은 아래와 같다:

  1. 입력에 대하여 MST(최소 신장 트리)를 찾는다.
  2. 임의의 도시로부터 출발하여 트리의 간선을 따라서 모든 도시를 방문하고, 다시 출발했던 도시로 돌아오는 도시 방문 순서를 찾는다. (백 트레킹 이용)
  3. 중복되어 나타나는 도시를 제거한 도시 순서를 return한다. (삼각 부등식의 원리를 이용하여 지금길로 도시 방문 순서를 만듦)

시간 복잡도는 MST를 찾는데 사용한 크러스컬 또는 프림 알고리즘의 시간 복잡도와 동일하다.
MST 간선의 가중치 합을 M이라고 할 때, 여행자 문제의 실제 최적해 값은 M보다 항상 크므로
M을 '간접적인' 최적해로 활용한다.
2번 단계에서 MST의 각 간선이 정확히 2번 사용되었으므로, 경로의 총 길이는 2M이 되고,
3번 단계에서 중복되는 도시를 제거하여 지름길로 도시 방문 순서를 만듦으로,
근사해의 값은 2M보다 작다.

따라서 이 알고리즘의 근사 비율은 2M/M=2.0보다 크지 않다.

#include <stdio.h>
#include <stdlib.h>
#define N 6
#define INF 10000
/* 신장 트리 */
int tree[N][N] = {
	{1,3,4,-1,-1,-1},
	{0,2,-1,-1,-1,-1},
	{1,5,-1,-1,-1,-1},
	{0,-1,-1,-1,-1,-1},
	{0,-1,-1,-1,-1,-1},
	{2,-1,-1,-1,-1,-1},
};
/* 간선의 가중치 배열*/
int g[N][N]={
	{0,3,INF,2,4,INF},
	{3,0,1,4,INF,2},
	{INF,1,0,INF,INF,1},
	{2,4,INF,0,5,7},
	{4,INF,INF,5,0,9},
	{INF,2,1,7,9,0},
};
/* 노드의 방문 여부를 저장하는 배열 */
int visited[N] = { 0 };
/* 방문 순서를 저장하는 배열 */
int path[2*(N-1)], index=0;

void dfs(int v) {
	visited[v] = 1;						// 노드 v에 방문 표시
	path[index++] = v;					// 노드 v를 경로에 추가
	for (int j = 0; j < N; j++) {		// 노드 v와 연결된 노드들을 차례로 방문
		if (tree[v][j] == -1)
			break;					
		if (!visited[tree[v][j]]) {		// 노드 v와 연결된 j번째 노드가 방문하지 않은 노드라면-> 방문
			dfs(tree[v][j]);
			path[index++] = v;			// 시작 노드로 되돌아감
		}
	}
}
/* list의 0~length-1 사이에 value가 존재하는지 알려주는 함수 */
int contains(int*list, int length, int value) {
	for (int i = 0; i < length; i++) {
		if (list[i] == value)
			return 1;
	}
	return 0;
}
/* 중복되는 노드 -> -1로 변경 */
void removeNode(int* path) {
	for (int i = 1; i < index; i++) {
		if(contains(path,i,path[i]))
			path[i] = -1;
	}
}
int main() {
	dfs(0);
	/* 트리 방문 순서 출력*/
	printf("트리 방문 순서: ");
	for (int i = 0; i < index; i++)
		printf("%d\t", path[i]);
	printf("\n");
	/* 중복되는 노드 -> -1로 변경 */
	removeNode(path);
	/* TSP 경로 출력 */
	printf("TSP 경로:\t");
	for (int i = 0; i < index; i++)
		if (path[i] != -1) {
			printf("%d\t", path[i]);
		}
	printf("%d\n",path[0]);
	/* TSP 경로의 길이 출력 */
	int weight, k;
	weight = 0;
	for (int i = 0; i < index - 1; i++) {
		if (path[i] != -1) {
			if (path[i + 1] != -1)
				weight += g[path[i]][path[i + 1]];
			else {						// 중복되는 노드는 pass
				k = 1;
				while (path[i + ++k] == -1) {}
				weight += g[path[i]][path[i + k]];
			}
		}
	}
	printf("appr dist = %d\n", weight);
}

(2) 정점 커버 문제

각 간선의 양 끝점들 중에서 적어도 하나의 끝점을 포함하는 점들의 집합들 중에서 최소 크기의 집합을 찾는 문제

극대 매칭(Maximal Matching) 방법을 이용하여 문제를 해결할 수 있다.
: 한 간선을 선택한 다음, 해당 간선의 양 끝점과 연결된 간선을 모두 제거한다.
이후, 간선의 양 끝점이 이미 커버된 간선의 끝점이 아닐 때에만 선택한다.

#include <stdio.h>
#include <stdlib.h>
#define N 6												// 정점의 개수
/* 간선 가중치 배열 */
int adj[N][N] = {
	{0,1,0,0,0,0},
	{1,0,1,1,1,0},
	{0,1,0,0,1,1},
	{0,1,0,0,0,0},
	{0,1,1,0,0,1},
	{0,0,1,0,1,0},
};
int visited[N] = { 0 };									// 커버된 간선의 끝점이면 1로, 아니면 0으로 표시
int C[N] = { -1 }, idx = 0;								// 정점 커버 배열
void VertexCover(int* C) {
	for (int i = 0; i < N; i++) {
		if (!visited[i]) {
			for (int j = 0; j < N; j++) {
				if (adj[i][j] != 0 && !visited[j]) {	// i와 j 사이에 간선이 존재하고, i와 j 모두 이미 커버된 간선의 끝점이 아닐 때
					C[idx++] = i;
					C[idx++] = j;
					visited[i] = 1;
					visited[j] = 1;
					break;								// 다음 i로 넘어감
				}
			}
		}
	}
}

int main() {
	VertexCover(C);
	for (int i = 0; i < idx; i++) {
		printf("%d\t", C[i]);
	}
	printf("\n");
}

(3) 통 채우기 문제

통의 용량이 C일 때, n개의 물건을 가장 적은 수의 통에 채우는 문제. (단, 각 물건의 크기는 C보다 크지 않다.)

그리디 방법은 '무엇에 욕심을 낼 것인가'에 따라 4종류로 분류한다.
각 방법으로 새 물건을 기존의 통에 넣을 수 없으면, 새로운 통에 새 물건을 담는다.

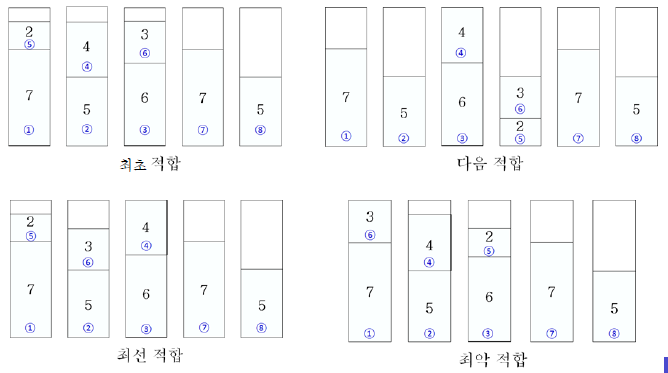
  • 최초 적합: 첫 번째 통부터 차례로 살펴보며, 가장 먼저 여유가 있는 통에 새 물건을 넣는다. O(n2)O(n^2)
  • 다음 적합: 직전에 물건을 넣은 통에 여유가 있으면 새 물건을 넣는다. O(n)O(n)
  • 최선 적합: 기존의 통 중에서 새 물건이 들어가면 남는 부분이 가장 작은 통에 새 물건을 넣는다. O(n2)O(n^2)
  • 최악 적합: 기존의 통 중에서 새 물건이 들어가면 남는 부분이 가장 큰 통에 새 물건을 넣는다. O(n2)O(n^2)

C=10이고, 물건의 크기가 [7, 5, 6, 4, 2, 3, 7, 5]일 때 각각의 방법을 적용한 결과는 아래와 같다 :

최초, 최선, 최악 적합의 근사 비율

최적해에서 사용된 통의 수를 OPT라고 하면, OPT = (모든 물건의 크기의 합)/C이다.
근사해에서 사용된 통의 수를 OPT'라고 하면, OPT'개의 통 중에서 기껏해야 2개의 통이 1/2 이하로 차 있으므로, (모든 물건의 크기의 합) > (OPT'-1)×\timesC/2
따라서, OPT >(OPT'-1)/2, 정리하면 2OPT+1 >OPT'에서 2OPT>=OPT'.
따라서 3가지 방법의 근사 비율은 2.0이다.

다음 적합의 근사 비율

이웃한 2개의 통에 들어있는 물건의 크기의 합은 C보다 크다.
(모든 물건의 크기의 합) > OPT'/2×/2\timesC
따라서, OPT >OPT'/2, 정리하면 2OPT >OPT'에서 근사 비율은 2.0이다

(4) 작업 스케줄링 문제

n개의 작업, m개의 기계가 있을 때
각 루프에서 m개의 기계 중 가장 작업이 빨리 끝나는 기계를 탐색하므로
시간 복잡도는 n×\timesO(m) = O(mn)이다.
T는 가장 마지막으로 배정된 작업 i가 수행되기 시작한 시간이고,
T'는 작업 i를 제외한 모든 작업의 수행 시간의 합을 기계의 수 m으로 나눈 값일 때

T<=T′T <= T'

(5) 클러스터링 문제

n개의 점을 k개의 그룹으로 나누고, 각 그룹이 중심이 되는 k개의 점을 선택하는 문제. 단, 가장 큰 반경을 가진 그룹의 직경이 최소가 되도록 k개의 점을 선택해야 한다.

k개의 센터를 선택하는 방법 :
첫 번째 센터: 임의의 점을 선택
두 번째 센터: 첫 번째 센터에서 가장 멀리 떨어진 점을 선택
세 번째 센터: 첫 번째와 두 번째 센터에서 가장 멀리 떨어진 점을 선택
...
의 과정을 k번 반복

이후 각 점을 가장 가까운 센터의 그룹으로 소속시켜준다.

시간 복잡도는 아래와 같다.
O(1)+(k−1)x(O(kn)+O(n))+O(kn)=O(k2n)O( 1 )+(k-1) x (O(kn)+O(n))+ O(kn)=O(k^2n)
OPT는 최적해가 만든 그룹 중에서 가장 큰 직경을 말한다.
k개의 센터를 모두 찾고 나서 (k+1)번째 센터를 찾았다고 하자.
이때, (k+1)번째 센터와 가장 가까운 센터까지의 거리를 d라고 하면 OPT>=d이다.
OPT'를 근사해가 만든 그룹 중에서 가장 큰 직경이라고 할 때, OPT'<=2d이다.
따라서 알고리즘의 근사 비율은 2.0이다.

profile
민정
이전 포스트

정렬 알고리즘

0개의 댓글