동적 계획(Dynamic Programming) 알고리즘

민정·2022년 5월 29일

알고리즘 이론 정리

목록 보기

4/6

동적 계획 알고리즘(Dynamic Programming)은 입력크기가 작은 부분 문제들을 해결한 후에, 그 해들을 이용하여 보다 큰 크기의 부분 문제들을 해결해나가는 알고리즘 방식이다. DP 알고리즘은 문제의 최적해 속에 부분 문제의 최적해가 포함되어 있음을 활용하며, 부분 문제의 해를 중복 사용하지 않는다.

동적 계획 알고리즘은 DP 배열을 생성하여 해당 배열에 부분 문제의 해를 저장하고, DP 배열의 값을 활용하여 보다 큰 크기의 부분 문제들을 구해나간다. 아래의 문제를 풀어보며 동적 계획 알고리즘을 이해해보자.

모든 쌍 최단 경로 문제

각 쌍의 점 사이의 최단 경로를 찾는 문제

그래프의 점이 1, 2, 3, ..., n일 때, $D_{ij}^{k}$ 의 의미는 다음과 같다.

$D_{ij}^{k} = 점\ \{1, 2, ..., k\}$ 를 경유 가능한 점으로 고려하여 점 $i$ 에서 점 $j$ 까지의 모든 경로 중에서 가장 짧은 경로의 거리

따라서 $k$ 가 1에서 $n$ 이 될 때까지 $D_{ij}^{k}$ 를 계산해서 $D_{ij}^{n}$ 을 찾는다. 의사 코드로 나타내면 아래와 같다.
시간 복잡도는 $O(n^3)$ 이다.

AllPairsShortest
입력: 2차원 배열 D, 단 D[i,j] = 간선 (i,j)의 가중치. 만일 간선 (i,j)가 없으면 D[i,j]= ∞, 모든 i에 대하여 D[i,i] = 0.
출력: 모든 쌍 최단 경로의 거리를 저장한 2차원 배열 D
1. for k=1 to n
2. for i=1 to n(i≠k)
3. for j=1 to n(j≠k, j≠i)
4. D[i,j] = min{D[i,k]+D[k+j], D[i,j]}

D[i, j]를 계산하기 위해서 미리 계산되어 있어야 할 부분 문제는 D[i, k]와 D[k, j]이다.
이렇듯 DP 알고리즘은 부분 문제 간의 함축적 순서를 이용하여 문제를 해결한다.

#include <stdio.h>
#define N 5
#define INFINITE 1000
#define MIN(x,y) ((x)>(y))?(y):(x)

int main() {
	int DP[N][N] = {							// 간선의 가중치로 DP배열 초기화 (k=0)
		{0,4,2,5,INFINITE},
		{INFINITE,0,1,INFINITE,4},
		{1,3,0,1,2},
		{-2,INFINITE, INFINITE,0,2},
		{INFINITE,-3,3,1,0}
	};
	for (int k = 0; k < N; k++) {
		for (int i = 0; i < N; i++) {
			if (i == k) continue;				// i != k
			for (int j = 0; j < N; j++) {	
				if (j == i || j == k) continue; // j !=i && j!=k
				DP[i][j] = MIN(DP[i][j], DP[i][k] + DP[k][j]);
			}
		}
	}
	// 각 쌍의 점 사이의 최단 경로 출력
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			printf("%d->%d의 최단 경로:%d \n", i+1, j+1, DP[i][j]);
		}
	}
}

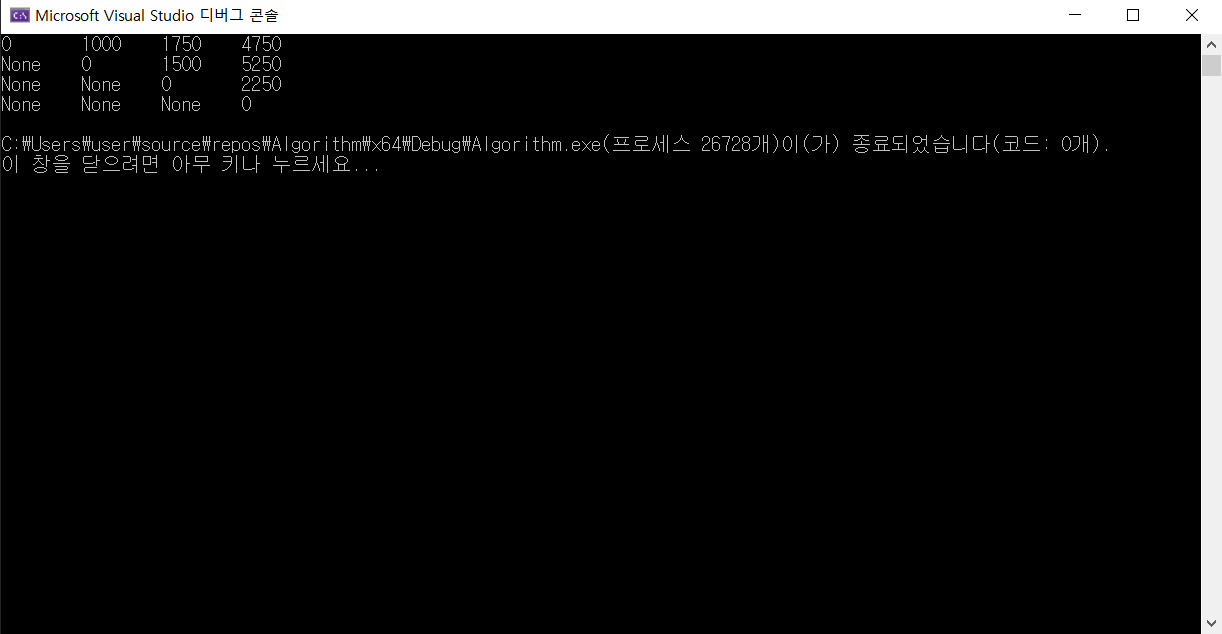
결과 화면은 아래와 같다.

연속 행렬 곱셈

연속된 행렬들의 곱셈에 필요한 원소 간의 최소 곱셈 횟수를 찾는 문제

행렬 A, B, C, D, E에 대하여 A×B×C×D×E를 계산한다면, 부분 문제의 크기와 개수는 아래와 같다.

이 원리를 확장하여, DP 알고리즘은 이웃하는 행렬들끼리 곱하는 모든 부분 문제들을 해결하여 최적해를 찾는다.
연속된 행렬 $A_{1}×A_{2}×...×A_{n}$ 에 대한 최소 곱셈 횟수를 찾는 알고리즘을 의사 코드로 작성하면 아래와 같다.
총 부분 문제 수는 $(n-1) + (n-2) + ... + 1 = n(n-1)/2$ 개이고, 하나의 부분 문제는 k-루프가 최대 (n-1)번 수행되므로, 시간 복잡도는 $O(n^2) \times O(n)=O(n^3)$ 이다.

입력: $A_{1}×A_{2}×...×A_{n}$ .
단, $A_{1}$ 은 $d_{0}×d_{1}$ , $A_{2}$ 은 $d_{1}×d_{2}$ ,..., $A_{n}$ 은 $d_{n-1}×d_{n}$ 이다.
출력: 입력의 행렬 곱셈에 필요한 원소의 최소 곱셈 횟수
$for\ i=1\ to\ n$
$\ \ \ \ \ \ C[i,i]=0$
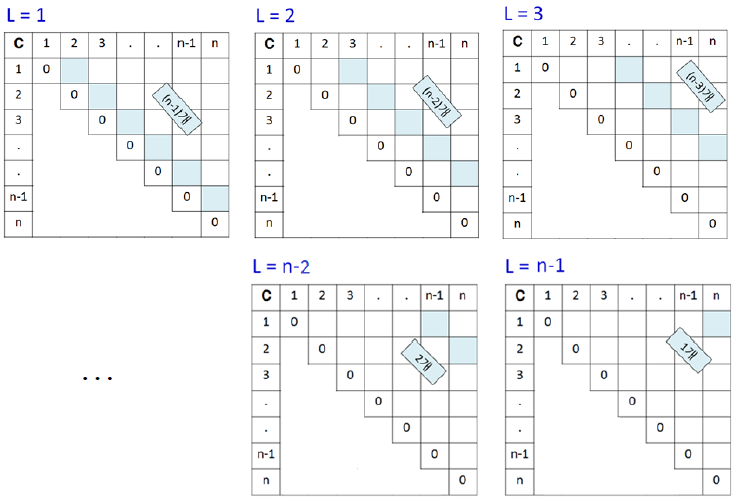
$for\ L=1\ to\ n-1$ // L은 부분 문제의 크기를 조절하는 인덱스
$\ \ \ \ \ \ for\ i=1\ to\ n-L$
$\ \ \ \ \ \ \ \ \ \ \ \ j=i+L$
$\ \ \ \ \ \ \ \ \ \ \ \ C[i,j] = ∞$
$\ \ \ \ \ \ \ \ \ \ \ \ for\ k=i\ to\ j-1$
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ temp = C[i, k] + C[k+1, j] + d_{i-1}d_{k}d_{j}$
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if(temp < C[i, j])$
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ C[i, j] = temp$
$return C[1, n]$

부분 문제의 크기는 L x (N-L)이 된다.

(1) $L=1$ 이라면 $i$ 와 $j$ 는 1씩 차이나므로,
$C[1][2]=(A_1) \times (A_2)$ 의 곱셈 횟수,
$C[2][3]=(A_2) \times (A_3)$ 의 곱셈 횟수,
...,
$C[N-1][N]=(A_{N-1}) \times (A_N)$ 의 곱셈 횟수

(2) $L=2$ 이라면 $i$ 와 $j$ 는 2씩 차이나므로,
$C[1][3]=(A_1) \times (A_2 \times A_3)$ 와 $(A_1 \times A_2) \times (A_3)$ 중 최소 곱셈 횟수,
$C[2][4]=(A_2) \times (A_3 \times A_4)$ 와 $(A_2 \times A_3) \times (A_4)$ 중 최소 곱셈 횟수,
...,
$C[N-2][N]=(A_{N-2}) \times (A_{N-3} \times A_{N-4})$ 와 $(A_{N-2} \times A_{N-3}) \times (A_{N-4})$ 중 최소 곱셈 횟수

와 같은 흐름으로 코드가 진행된다.

#include <stdio.h>
#define N 4
#define INFINITE 10000
#define MIN(x,y) ((x)>(y))?(y):(x)

int main() {
	int j;
	int C[N][N];						// 행렬 A0xA1x...xA(N-1)
	int d[N + 1] = { 10,20,5,15,30 }; 	// 행렬 A_p는 d[p]xd[p+1] 크기의 행렬이다.

	for (int i = 0; i < N; i++) {
		C[i][i] = 0;
	}
	// L: 부분 문제의 크기를 조절. 루프 내에서 부분 문제의 크기는 L x (N-L).
	for (int L = 1; L <= N - 1; L++) {
		for (int i = 0; i < N - L; i++) {
			j = i + L;
			C[i][j] = INFINITE;
			for (int k = i; k < j; k++) {
				C[i][j] = MIN(
					C[i][j],
					C[i][k] + C[k + 1][j] + d[i] * d[k + 1] * d[j + 1]
				);
			}
		}
	}
	for (int i = 0; i < N; i++) {
		for (j = 0; j < N; j++) {
			if (i <= j)
				printf("%d\t", C[i][j]);
			else
				printf("None\t");
		}
		printf("\n");
	}
	
}

편집 거리 문제

편집 거리(Edit Distance)를 찾는 문제

편집 거리(Edit Distance)는 삽입, 삭제, 대체(substitute) 연산을 사용하여 문자열 S를 수정하여 다른 문자열 T로 변환하고자 할 때 필요한 최소 편집 연산 횟수를 의미한다.
예를 들어, "spring"을 "strong"으로 변환한다면, 's'는 그대로 사용, 'p'는 't'로 대체, 'r'은 그대로 사용, 'i'는 'o'로 대체, 'n'과 'g'는 그대로 사용하여 총 2회의 편집 연산을 수행한다. 다양한 편집 횟수가 나타날 수 있으며, 최소 편집 횟수를 편집 거리라고 부른다.
부분 문제의 정의는 아래와 같다.

E[i, j] = S의 처음 i개 문자를 T의 처음 j개 문자로 바꾸는데 필요한 편집 거리
(ex) "strong"을 "stone"으로 변환할 때, "stro"를 "sto"로 바꾸기 위한 편집 거리는 E[4, 3]이다.

E[i, j]는 아래와 같이 표현할 수 있다.

E[i,j] = E[i-1, j] +1
: S의 [i]에서 $s_i$ 를 삭제하면 S의 [i-1]를 T의 [j]로 변환하는 상태와 같아지므로, $s_i$ 의 삭제 연산 횟수 1을 더해준다.
E[i,j] = E[i, j-1] +1
: S의 [i]를 T의 [j-1]로 변환한 다음, $t_j$ 를 삽입하면 되므로, $t_j$ 의 삽입 연산 횟수 1을 더해준다.
E[i,j] = E[i-1, j-1] + a( $s_i$ = $t_j$ 이면 a=0, 아니면 a=1)
: $s_i$ 를 $t_j$ 로 대체하면 되므로, $s_i$ 와 $t_j$ 가 다를 경우 대체 연산 횟수 1을 더해준다.

따라서 편집 거리 E[i, j]는 위의 3가지 표현식의 최솟값으로 구하면 된다.

#include <stdio.h>
#define N 6
#define M 5
#define MIN(x,y,z) (((x)>(y))?(y):(x))>(z)?z:(((x)>(y))?(y):(x))

int main() {
	int a;
	char S[] = "strong";
	char T[] = "stone";
	int E[N][M];
	for (int i = 0; i < N; i++) {	// 0번 열 초기화
		E[i][0] = i;
	}
	for (int j = 0; j < M; j++) {	// 0번 행 초기화
		E[0][j] = j;
	}
	for (int i = 1; i < N; i++) {
		for (int j = 1; j < M; j++) {
			a = S[i] == T[j] ? 0 : 1;
			E[i][j] = MIN(
				E[i-1][j]+1, E[i][j-1]+1, E[i-1][j-1]+a
			);
		}
	}
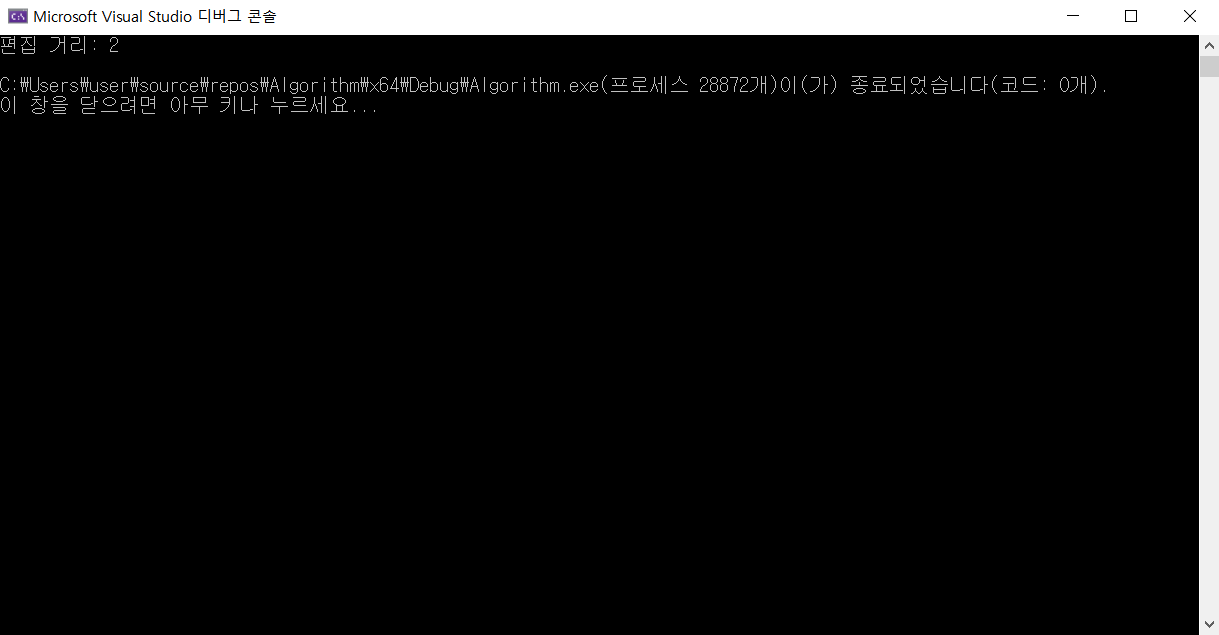
	printf("편집 거리: %d\n", E[N - 1][M - 1]);
}

N으로 표현

(1) 문제 설명

아래와 같이 5와 사칙연산만으로 12를 표현할 수 있습니다.

12 = 5 + 5 + (5 / 5) + (5 / 5)
12 = 55 / 5 + 5 / 5
12 = (55 + 5) / 5

5를 사용한 횟수는 각각 6,5,4 입니다. 그리고 이중 가장 작은 경우는 4입니다.
이처럼 숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 표현 할 수 있는 방법 중 N 사용횟수의 최솟값을 return 하도록 solution 함수를 작성하세요.

(2) 제한사항

N은 1 이상 9 이하입니다.

number는 1 이상 32,000 이하입니다.

수식에는 괄호와 사칙연산만 가능하며 나누기 연산에서 나머지는 무시합니다.

최솟값이 8보다 크면 -1을 return 합니다.

(3) 풀이 설명

DP 배열에는 N을 k+1번 사용한 수들의 집합을 저장한다.
(ex)
5를 2번 사용한 수는 55, 5/5, 5+5, ...
5를 3번 사용한 수는 555, 55/5, 55+5, ...
5를 4번 사용한 수는 5555, 555/5, 555+5, 55+55, ...

이들을 일반화하면 다음과 같다.
사칙 연산이 들어가는 자리를 ㅁ로 표시하면,

5를 2번 사용한 수 = {55, (5를 1번 사용한 수)ㅁ(5를 1번 사용한 수)}
5를 3번 사용한 수 = {555, (5를 1번 사용한 수)ㅁ(5를 2번 사용한 수), (5를 2번 사용한 수)ㅁ(5를 1번 사용한 수)}
5를 4번 사용한 수 = {5555, (5를 1번 사용한 수)ㅁ(5를 3번 사용한 수), (5를 2번 사용한 수)ㅁ(5를 2번 사용한 수), (5를 3번 사용한 수)ㅁ(5를 1번 사용한 수)}

따라서 DP[0] ~ DP[k-1]을 이용하여 DP[k]를 구한다.
만약 DP[k]의 원소에 number가 포함되어있다면 k+1을 return한다.

(4) 사용한 자료구조

각 DP[i]는 unordered_set 자료구조로 나타내었다.
DP 배열은 원소의 추가와 삭제가 자유로운 vector 자료구조로 나타내었다.

unordered_set와 set 자료구조는 중복을 허용하지 않는다는 공통점이 있지만,
unordered_set은 set과 달리 자동 정렬 기능이 지원되지 않는다.

N을 k+1번 사용하는 수들의 집합을 저장하는데 정렬 기능은 필요하지 않으므로,
set이 아닌 unordered_set을 이용하여 DP[i]를 나타내었다.

unordered_set 클래스에 대한 자세한 내용은 아래 링크에서 확인할 수 있다.
여기서 눈여겨봐야할 Function은 insert와 count이다.
#include <unordered_set>으로 unordered_set 클래스를 불러온 다음, 해당 클래스를 사용할 수 있다.
https://docs.microsoft.com/ko-kr/cpp/standard-library/unordered-set-class?view=msvc-170

#include <string>
#include <vector>
#include <unordered_set>                // 중복된 원소 허용 x, 정렬이 자동으로 되지 않음.
using namespace std;
int getNN(int N, int idx){
    int result = N;
    for(int i=1; i<=idx; i++){
        result = result*10 + N;
    }
    return result;
}
int solution(int N, int number) {
    if(N==number)
        return 1;
    vector<unordered_set<int>> DP(8);   // DP[k]: N을 k+1번 사용한 수들의 집합
    DP[0].insert(N); 
    for(int k=1; k<8; k++){
        for(int i=0; i<k;i++){
            for(int D1 : DP[i]){        // (j+1) = (k+1) - (i+1)
                for(int D2 : DP[k-i-1]){
                    DP[k].insert(D1+D2);
                    if(D1>D2) DP[k].insert(D1-D2);      // N의 최소 개수로 number를 만드는 것이 목표이기 때문에 0은 불필요한 값 => D1 - D2 > 0인 경우에만 insert
                    DP[k].insert(D1*D2);
                    if(D1/D2>0) DP[k].insert(D1/D2);    // 나누기 연산에서 나머지는 무시함.
                }
            }
        }
        DP[k].insert(getNN(N,k));
        
        if(DP[k].count(number))         // 값이 number인 원소가 존재한다면 k+1을 return
            return k+1;
    }
    return -1;                          // 최솟값이 8보다 크면 -1을 return       
}

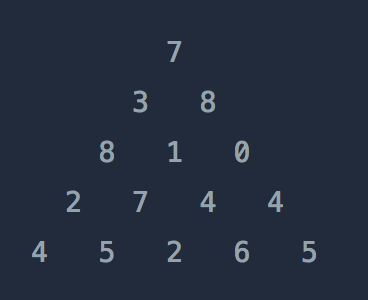
정수 삼각형

(1) 문제 설명

위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

(2) 제한사항

삼각형의 높이는 1 이상 500 이하입니다.
삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.

(3) 입출력 예

(4) 풀이 설명

삼각형의 꼭대기를 0층의 0열이라고 할 때,
$DP[i][j]$ 에는 꼭대기에서 i층의 j열까지 거쳐간 숫자의 합 중 가장 큰 값을 저장한다.

일단 모든 $i$ 층의 $0$ 열은 0층에서 i-1층까지의 0열을 모두 더한 값이므로 $DP[i-1][0] + triangle[i][0]$ 으로,
$i$ 열은 0층에서 i-1층까지의 마지막 열을 모두 더한 값이므로 $DP[i-1][i-1] + triangle[i][i]$ 로 구한다.

나머지 $DP[i][j]$ 는 $triangle[i-1][j-1]$ 혹은 $triangle[i-1][j]$ 에서 내려온 경로의 숫자 합이므로,
DP[i-1][j-1]와 DP[i-1][j]중 큰 값과 triangle[i][j]를 더한 값으로 구한다.

이후 DP배열의 바닥 층 중에서 가장 큰 값을 가진 열의 값을 return한다.

#include <string>
#include <algorithm>
#include <vector>
#define M 500
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
using namespace std;

int solution(vector<vector<int>> triangle) {
    int DP[M][M];                           // DP 배열
    DP[0][0] = triangle[0][0];
    int max = -1; 
    for(int i=1; i<triangle.size(); i++){  
        DP[i][0] = DP[i-1][0] + triangle[i][0];
        DP[i][i] = DP[i-1][i-1] + triangle[i][i];
    }
    for(int i=2; i<triangle.size(); i++){
        for(int j=1; j<i; j++){
            DP[i][j]=MAX(DP[i-1][j-1],DP[i-1][j])+triangle[i][j]; 
        }
    }
    for(int i=0; i<triangle.size(); i++)   // 가장 큰 숫자의 합 구하기
        max = MAX(DP[triangle.size()-1][i], max);

    return max;
}

민정

이전 포스트

그리디(Greedy) 알고리즘

다음 포스트