HW3

1. 스케줄링 문제에 접근하는 이진 탐색 트리 소개

먼저 탐색(search)에 대해 알아보자. 탐색은 가장 중요한 컴퓨터 응용의 하나이다. 핵심 응요으로 많은 프로그램에서 구현되어 사용되고 있는 기능이다. 정보량의 급속한 증가에 따라 원하는 정보를 빠르고 효율적으로 탐색하는 것이 중요하다.

이진 탐색 트리(BST, Binary Search Tree)는 이진트리 기반의 탐색을 위한 자료구조로 효율적인 탐색 작업을 위한 자료구조이다. 이진 탐색 트리는 특별한 성질을 만족하는 이진 트리를 말하는데, 다음과 같이 정의된다.

· 모든 노드는 유일한 키를 갖는다.
· 왼쪽 서브트리의 키들은 루트의 키보다 작다.
· 오른쪽 서브트리의 키들은 루트의 키보다 크다.
· 왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.

기본적인 정의는 key(왼쪽 서브트리)≤key(루트 노드)≤key(오른쪽 서브트리)로 표현된다. 이진탐색을 중위순회하면 오름차순으로 정렬된 값을 얻을 수 있다.

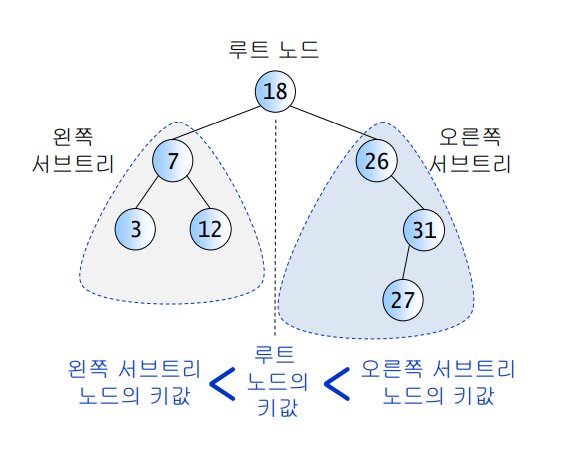
위의 사진은 이진 탐색 트리라고 할 수 있을까? 왼쪽 서브트리에 있는 값들(3, 7, 12)은 루트노드인 18보다 작다. 또한, 오른쪽 서브트리에 있는 값들(26, 31, 27)은 루트 노드인 18보다 크다. 이 성질은 모든 노드에서 만족되기 때문에 이진 탐색 트리이다.

2. Big-O 소개

가장 헷갈리고 어렵게 느껴졌던 부분이다. 시간 복잡도 함수에서 중필요한 것은 n에 대해 연산이 몇 번 필요한가가 아니라 n이 증가함에 따라 무엇에 비례하는 수의 연산이 필요한가이다. 시간 복잡도 함수에서 불필요한 정보를 제거하여 알고리즘 분석을 쉽게 할 목적으로 시간 복잡도를 표시하는 방법을 빅오 표기법이라고 한다. 즉, 알고리즘이 n에 비례하는 실행 시간을 가진다고 말할 때 알고리즘 A의 시간 복잡도가 O(n)이라고 한다.

int f(int n) {
	int i, m = 0;
    i = 1;
    while (i < n) {
    	m += 1;
        i = i * 2;
    }
    return m;
}

코드를 통해 자세히 살펴보자. 이 코드의 시간 복잡도를 먼저 말하자면 O(logn)으로 표현된다. 절반으로 나누는 것을 통해 알 수 있다.

빅오 표기법의 실행 시간을 비교하면 아래와 같다. 결국은 입력의 개수에 따른 기본 연산의 수행 횟수를 개략적으로 나타낸 것으로 알고리즘의 성능을 비교할 수 있다.

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n!)

3. 문제 풀이

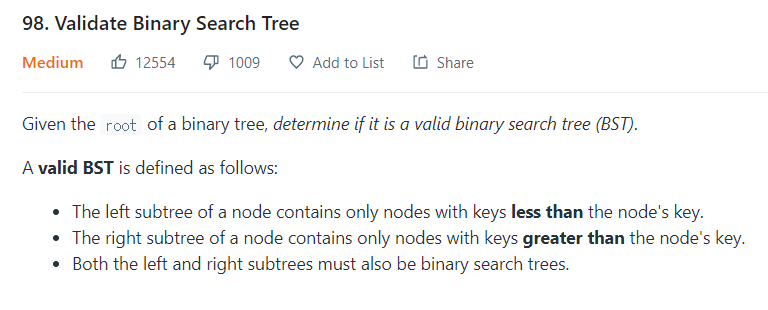
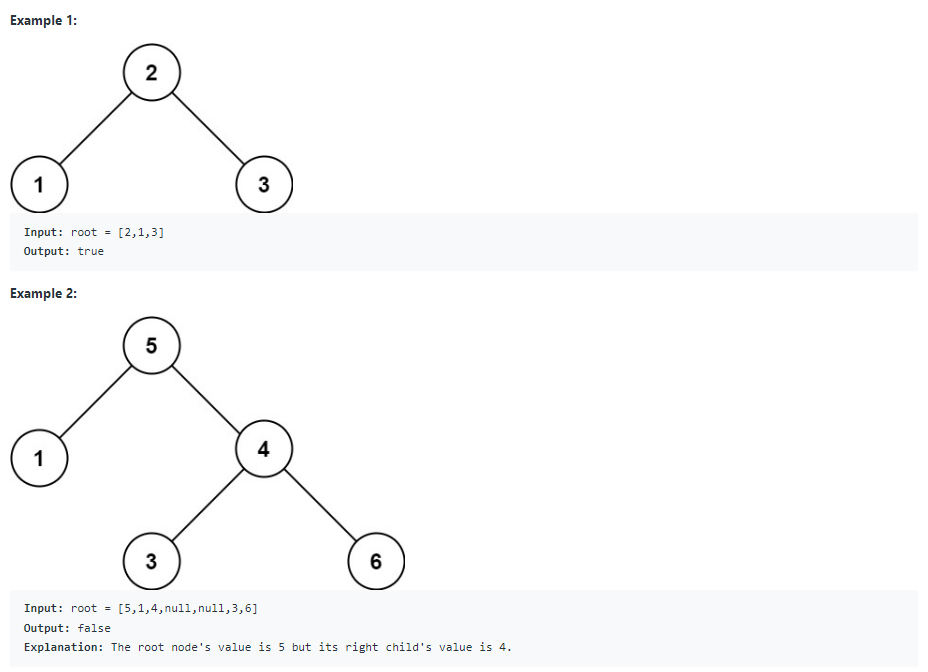
3.1. LeetCode 98

[문제 정리]

· 유효한 BST는 다음과 같이 정의된다:
· 노드의 왼쪽 서브 트리는 노드의 키보다 작은 키를 가진 노드만 포함한다.
· 노드의 오른쪽 서브 트리는 노드의 키보다 작은 키를 가진 노드만 포함한다.
· 왼쪽과 오른쪽의 서브 트리는 또한 이진 탐색 트리여야 한다.

[풀이]

class Solution {
public:
    bool isValidBST(TreeNode* root, TreeNode* low, TreeNode* high) {
        if(!root) return true;
        
        if(low && root->val <= low->val) 
            return false;
        if(high && root->val >= high->val) 
            return false;
        
        return isValidBST(root->right, root, high) && isValidBST(root->left, low, root);
    }
    
    bool isValidBST(TreeNode* root){
        return isValidBST(root, nullptr, nullptr);
    }
};

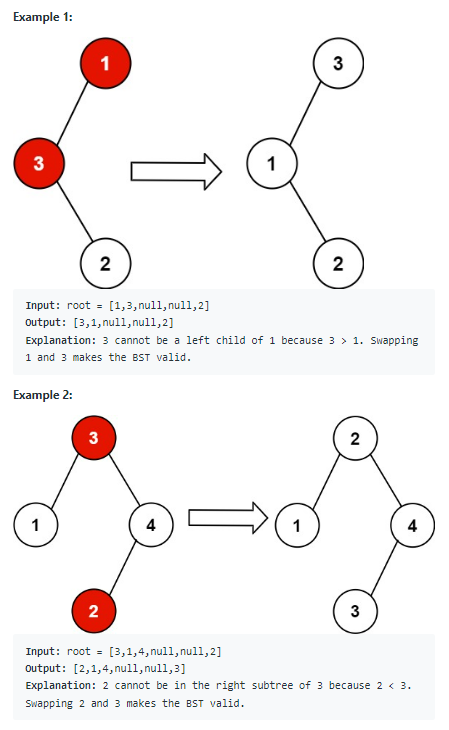
3.2. LeetCode 99

class Solution {
public:
    void recoverTree(TreeNode* root) {
        inorder(root);
        swap(first->val, second->val);
    }
    
    void inorder(TreeNode* root){
        if(!root) return;
        inorder(root->left);
        if(prev && prev->val > root->val){
            if(!first) first = prev;
            second = root;
        }
        prev = root;
        inorder(root->right);
    }
private:
    TreeNode* first;
    TreeNode* second;
    TreeNode* prev;
};

3.3. LeetCode 700

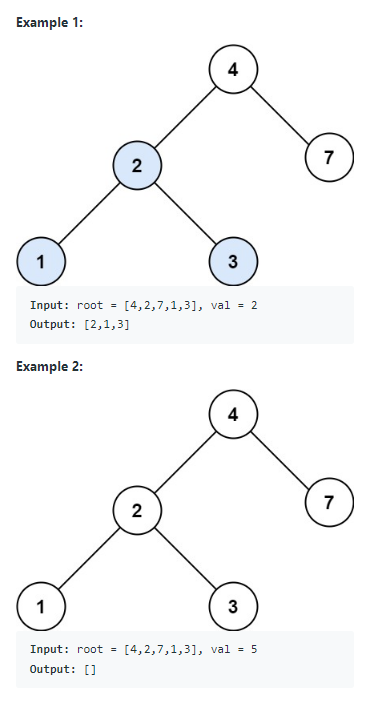
[문제 정리]

· Example 1: val값이 2인 것을 찾는다. 존재하므로 2와 그것의 sub트리까지 출력한다.
· Example 2: val값이 5인 것을 찾는다. 없기 때문에 null값을 출력한다.

[풀이]

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root==NULL){
            return NULL;
        }else if(root->val==val){
            return root;
        }else if(val < root->val){
            return searchBST(root->left, val);
        }else{
            return searchBST(root->right, val);
        }
    }
};

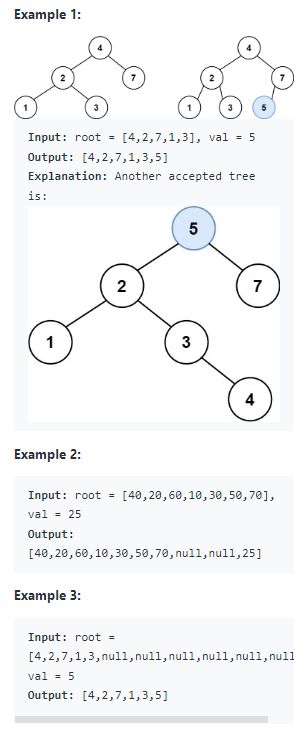
3.4. LeetCode 701

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        TreeNode* t = new TreeNode(val);
        if(!root) 
            return t;
        if(root->val < val)
            root->right = root->right ? insertIntoBST(root->right, val):t;
        else
            root->left = root->left ? insertIntoBST(root->left, val):t;
        return root;
    }
};