HW4

1. Data structures augmentation

1.1 Rank 구현

순위(Rank) 알고리즘은 지정된 범위중에서 순위를 구할 때 사용한다. 갯수(count) 알고리즘을 응용했으며 모든 점수는 처음에는 1등으로 설정한 후 해당 점수보다 큰 점수가 나타날 때마다 등수를 1씩 증가시켜 순위를 낮추는 것이 중요하다. scores[i]와 scores[j]를 비교하여 rank를 ++한다는 뜻이다.

#include <iostream>
using namespace std;
  
int main()
{
  
    cout << "rank of following type:"
         << endl;
    cout << "int: "
         << rank<int>::value
         << endl;
  
    cout << "int[]: "
         << rank<int[]>::value
         << endl;
  
    cout << "int[][10]: "
         << rank<int[][10]>::value
         << endl;
  
    cout << "int[10][10]: "
         << rank<int[10][10]>::value
         << endl;
  
    return 0;
}

1.2 AVL tree 구현

· 이진 탐색 트리 클래스를 상속한 AVL 트리 클래스

#include "BinSrchTree.h"
classs AVLTree : public BinSrchTree
{
public:
        int getHeightDiff(BinaryNode *node){
            if(node==NULL) return 0;
            int hLeft = getHeight(node->getLeft());
            int hRight = getHeight(node->getRight());
            return hleft - hRight;
        }
        
        // LL 회전 함수
        BinaryNode *rotateLL(BinaryNode* parent){
            BinaryNode* child = parent->getLeft();
            parent->setLeft(child->getRight());
            child->setRight(parent);
            return child;
        }
        
        // RR 회전 함수
        BinaryNode *rotateRR(BinaryNode* parent){
            BinaryNode* child = parent->getRight();
            parent->setLeft(child->getLeft());
            child->setLeft(parent);
            return child;
        }
        
        // RL 회전 함수
        BinaryNode *rotateRL(BinaryNode* parent){
            BinaryNode* child = parent->getRight();
            parent->setLeft(rotateRR(child));
            return rotateRR(parent);
        }
        
        // LR 회전 함수
        bINARYnODE *rotateLR(BinaryNode* parent){
            BinaryNode* child = parent->getLeft();
            parent->setLeft(rotateRR(child));
            return roatateLL(parent);
        }
        
        BinaryNode *reBalance(BinaryNode *parent){
            int hDiff=getHeightDiff(parent);
            if(hDiff>1){
                if(getHeightDiff(parent->getLeft())>0)
                    parent=rotateLL(parent);
                else parent=rotateLR(parent);
            }
            else if(hDiff<-1){
                if(getHeightDiff(parent->getRight())<0)
                    parent=rotateRR(parent);
                else paretn=rotateRL(parent);
            }
            return parent;
        }
        // AVL 트리의 삽입 연산
        void insert(int data){
            if(isEmpty()) root = new BinaryNode(data);
            else root = insertAVL(root, data);
        }
        
        BinaryNode* insertAVL(BinaryNode* parent, int data){
            if(data<parent->getData()){
                if(parent->getLeft() != NULL)
                    parent->setLeft(insertAVL(parent->getLeft(), data));
                    
                else
                    parent->setLeft(new BinaryNode(data));
                return reBalance(parent);
            }
            else if(data>parent->getData()){
                if(parent->getRight()!=NULL)
                    parent->setRight(insertAVL(parent->getRight(), data));
                else 
                    parent->setRight(new BinaryNode(data));
                return reBalnce(parent);
            }
            else{
                printf("중복된 키 에러\n");
                return NULL;
            }
        }
};

· 이진 탐색 트리 클래스와 이를 상속한 AVL 클래스

#include "AVLTree.h"
void main(){
    AVLTree tree;
    
    tree.insert( 7);    tree.levelorder();
    tree.insert( 8);    tree.levelorder();
    tree.insert( 9);    tree.levelorder();
    tree.insert( 2);    tree.levelorder();
    tree.insert( 1);    tree.levelorder();
    tree.insert( 5);    tree.levelorder();
    tree.insert( 3);    tree.levelorder();
    tree.insert( 6);    tree.levelorder();
    tree.insert( 4);    tree.levelorder();
}

출처: c++로 쉽게 풀어쓴 자료구조

2. AVL tree

이진 탐색 트리의 탐색 연산은 트리의 높이를 하나씩 더해갈수록 추가할 수 있는 노드의 수가 두 배씩 증가하므로, 이진 탐색 트리는 O(log_2n)의 시간복잡도를 가진다. 그런데 이러한 이진 탐색 트리는 균형이 맞지 않을수록 O(n)에 가까운 시간 복잡도를 보인다.

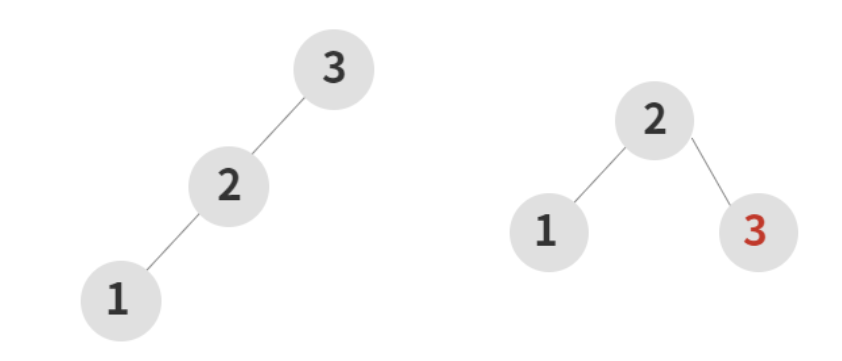
왼쪽 그림에서는 1부터 3까지 순서대로 저장되었을 때의 이진 탐색 트리이다. 이진 탐색 트리의 조건을 만족하지만, 노드 수에 가까운 높이를 형성한다. 오른쪽 그림처럼 저장 순서만 바꿨더니 루트 노드를 기준으로 어느 정도 균형이 잡혔고 트리의 높이도 줄었다는 것을 알 수 있다. 이진 탐색 트리는 저장 순서에 따라 성능에 큰 차이가 있다.

AVL 트리는 각 노드에서 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가 1 이하인 이진 탐색 트리를 말한다. 트리가 비균형 상태가 되면 스스로 노드들을 재배치하여 균형 상태로 만든다. 항상 균형 트리를 보장하기 때문에 O(logn)의 탐색 시간을 보장한다.

AVL 트리에서 균형이 깨지는 경우는 4가지 타입이 있다.

· LL 타입: N이 A의 왼쪽 서브트리의 왼쪽 서브트리에 삽입된다.
· LR 타입: N이 A의 왼쪽 서브트리의 오른쪽 서브트리에 삽입된다.
· RR 타입: N이 A의 오른쪽 서브트리의 오른쪽 서브트리에 삽입된다.
· RL 타입: N이 A의 오른쪽 서브트리의 왼쪽 서브트리에 삽입된다.

각각의 경우에 대하여 균형 트리로 다시 만드는 방법이다.

· LL 타입: A부터 N까지의 경로상의 노드들을 오른쪽으로 회전시킨다.
· LR 타입: A부터 N까지의 경로상의 노드들을 왼쪽-오른쪽으로 회전시킨다.
· RR 타입: A부터 N까지의 경로상의 노드들을 왼쪽으로 회전시킨다.
· RL 타입: A부터 N까지의 경로상의 노드들을 오른쪽-왼쪽으로 회전시킨다.

이제 4개의 회전 방법에 대한 자세한 설명을 하겠다.

2.1 LL 회전

6, 5, 2 순으로 노드를 삽입했을 경우에 만들어진다. 노드 6은 균형 인수가 2로서 불균형하다. 오른쪽으로 회전을 시키면 균형 트리를 만들 수 있다.

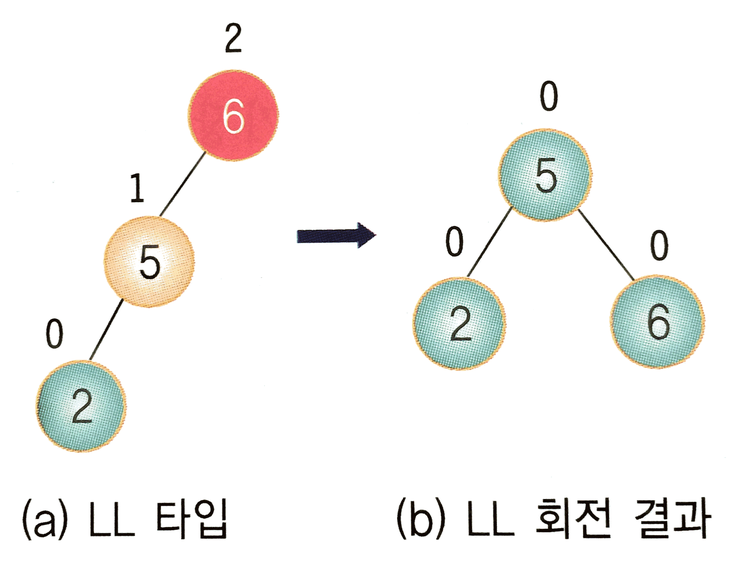
일반적인 LL 타입은 조상 노드 A의 왼쪽 서브트리의 왼쪽 서브트리에 노드가 추가됨으로 해서 발생한다. LL 회전은 노드들을 오른쪽으로 회전시키면 된다.

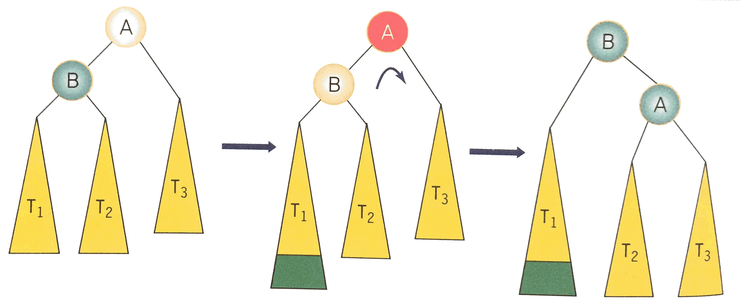
2.2 RR 회전

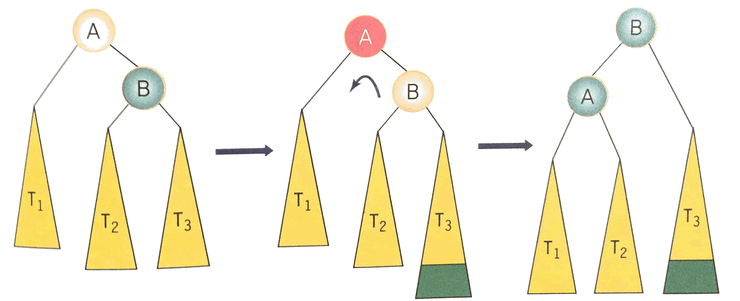
트리를 왼쪽으로 한번 회전하면 균형 트리로 만들 수 있다. 부모 노드와 자식 노드를 바꾸면 된다.

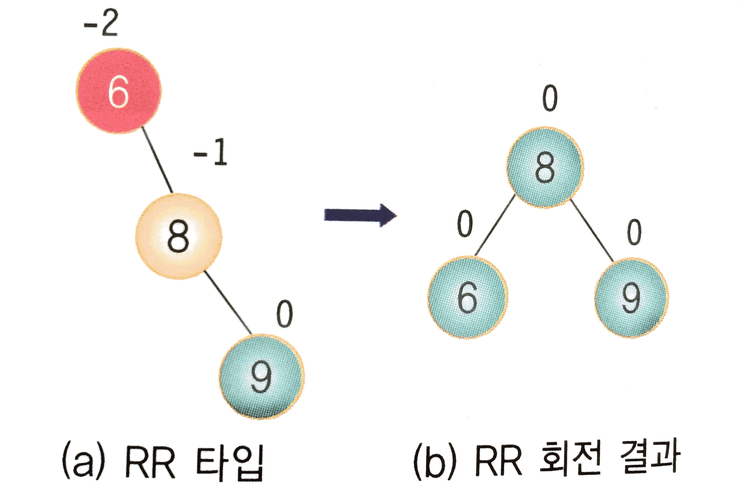
조상 노드 A의 오른쪽 서브트리의 오른쪽 서브트리에 노드가 추가됨으로 발생한다. 노드 A, B의 위치를 바꾸고 서브트리들을 정리하면 균형트리를 만들 수 있다.

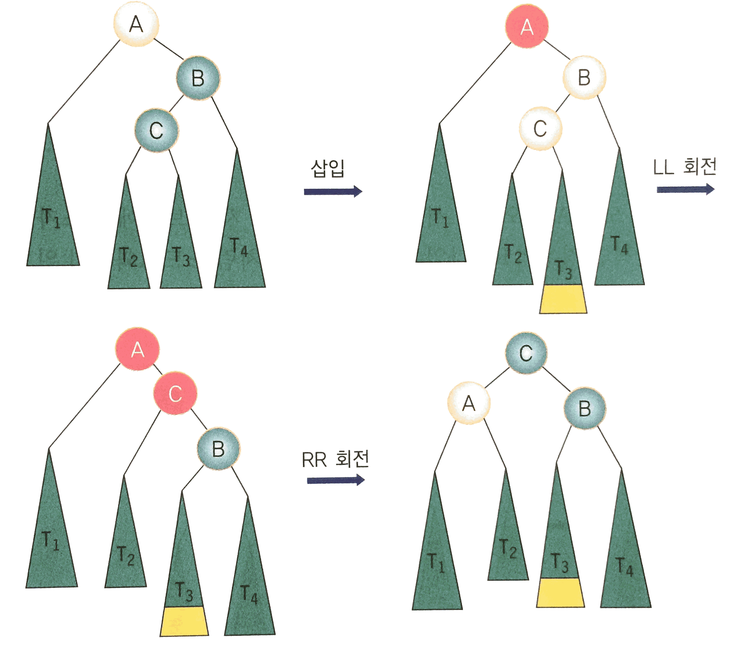
2.3 RL 회전

조상 노드 A의 오른쪽 서브트리의 왼쪽 서브트리에 노드가 추가됨으로 해서 발생한다. RL 회전은 균형 트리를 만들기 위하여 2번의 회전이 필요하다. 먼저 LL 회전을 하고, RR 회전을 하면 된다.

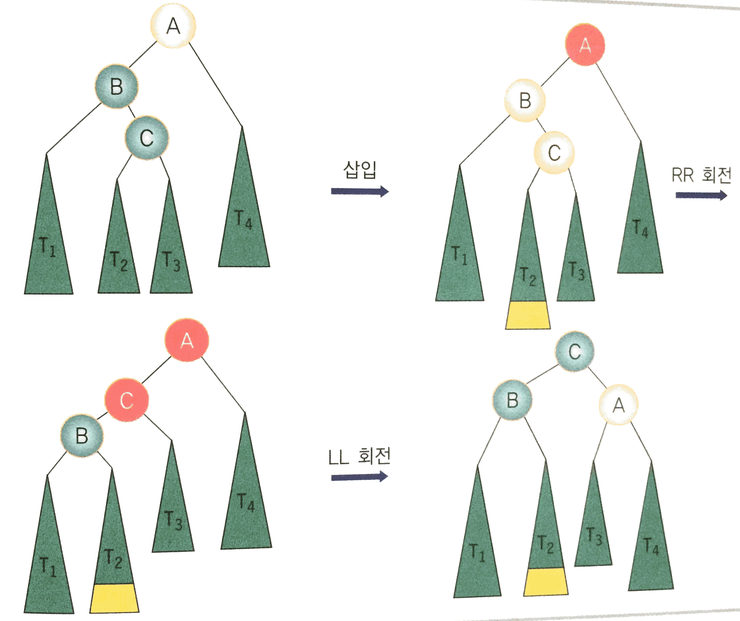
2.4 LR 회전

조상 노드 a의 왼쪽 서브트리의 오른쪽 서브트리에 노드가 추가됨으로 해서 발생한다. LR 회전은 균형 트리를 만들기 위하여 2번의 회전이 필요하다. 먼저 RR회전을 하고, LL 회전을 하면 된다.

3. 문제 풀이

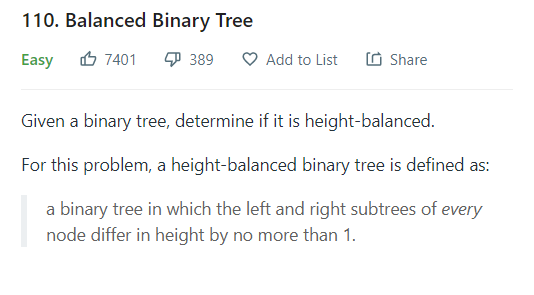
3.1 LeetCode 110

[문제]

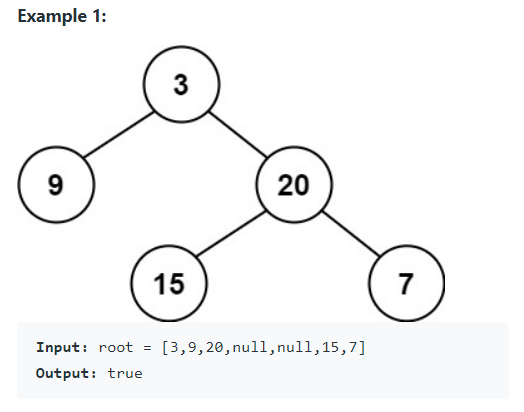
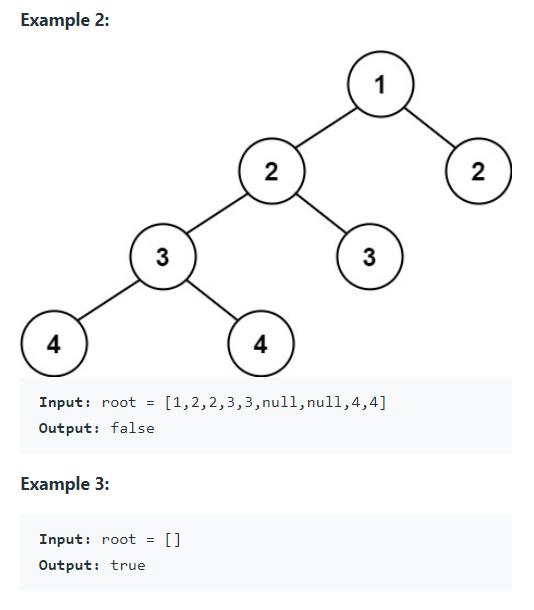
[문제 정리]

· 이진 트리가 높이 균형(Height-Balanced)인지 파악합니다.
· 트리의 모든 자식의 높이가 1 이상 차이가 날 경우 Fase, 아닌 경우 True를 반환합니다.

[풀이]

class Solution {
public:
    int getHeight(TreeNode* root){
        if(!root) return 0;
        int leftHeight = getHeight(root->left);
        int rightHeight = getHeight(root->right);
        int balanceFactor = abs(leftHeight-rightHeight);
        if(balanceFactor>1 || leftHeight==-1 || rightHeight==-1) return -1;
        return 1 + max(leftHeight, rightHeight);
    }
    bool isBalanced(TreeNode* root){
        if(!root) return true;
        return getHeight(root)==01 ? false : true;
    }
};