1. BFS
1.1 개념
너비 우선 탐색(Breadth First Search) 줄여서 BFS로 쓴다. 너비 우선 탐색은 너비를 우선으로 하여 자신에게 연결된 가까운 사람들부터 모든 사람에게 연락을 취하는 방식이다. 맹목적인 탐색을 하고자 할 때 사용할 수 있는 탐색 기법미여 최단경로를 찾아준다는 점에서 최단 길이를 보장해야 할 때 많이 사용한다.
·장점
·DFS과 다르게 최적해를 찾음을 보장한다.
·단점
·최소 실행 시간보다는 오래 걸린다는 것이 거의 확실하다.
·최악의 경우, 실행에 가장 긴 시간이 걸릴 수 있다.1.2 방법
ex) 그래프의 노드 A를 시작 노드로 설정하여 BFS를 이용하여 탐색한다고 가정
step1. 처음 시작 노드 방문 (A)
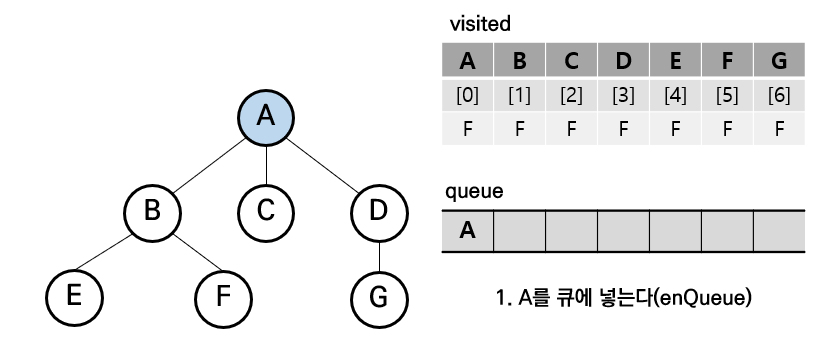
step2. A는 큐에서 삭제 및 방문 표시 후 A의 인접 노드들을 큐에 삽입
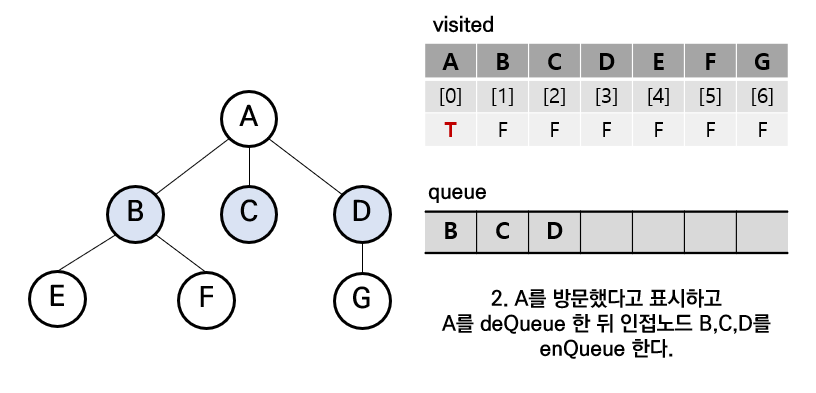
step3. A의 인접노드들 중 가장 큐에 먼저 들어간 B를 큐에서 삭제 및 방문 표시, B의 인접 노드들을 큐에 삽입
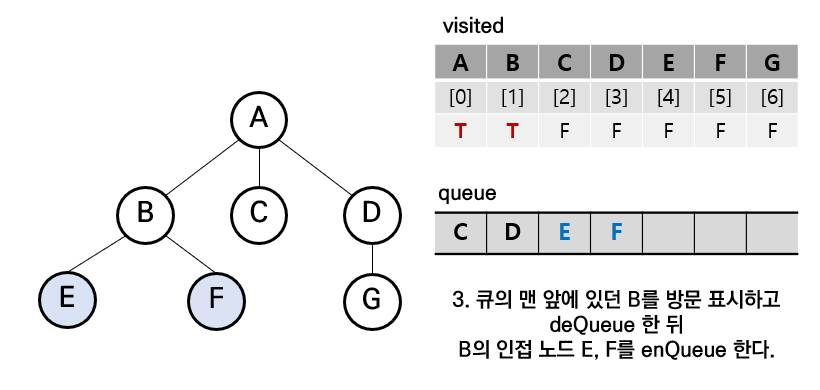
step4. C를 큐에서 삭제 및 방문 표시, C의 인접 노드를 큐에 넣으려 했으나 없으므로 skip
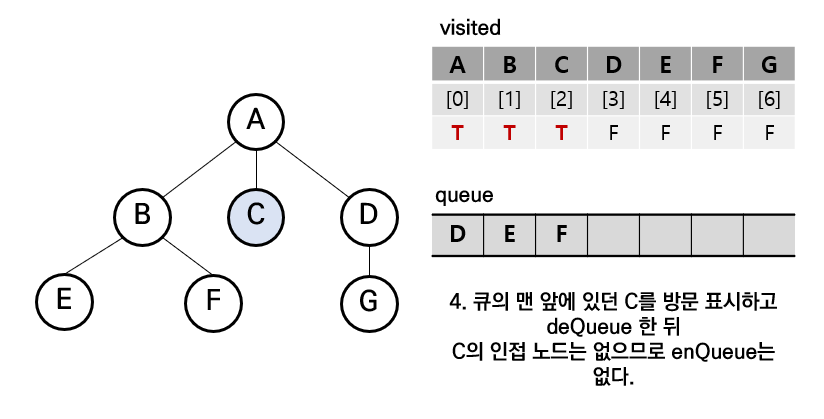
step5. 마찬가지로 D도 큐에서 삭제 및 방문 표시, D의 인접 노드 G를 큐에 삽입
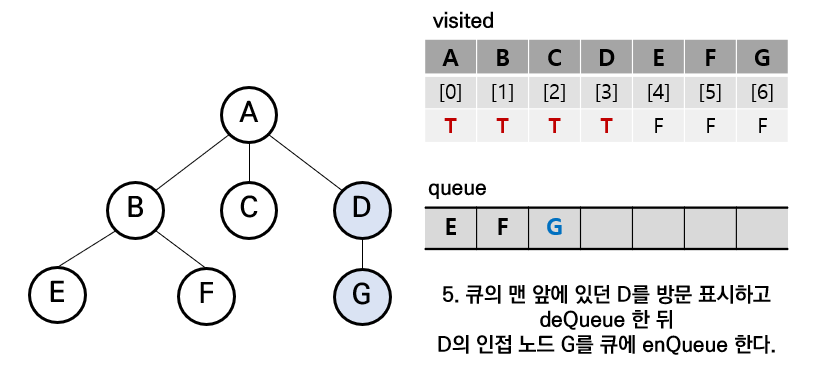
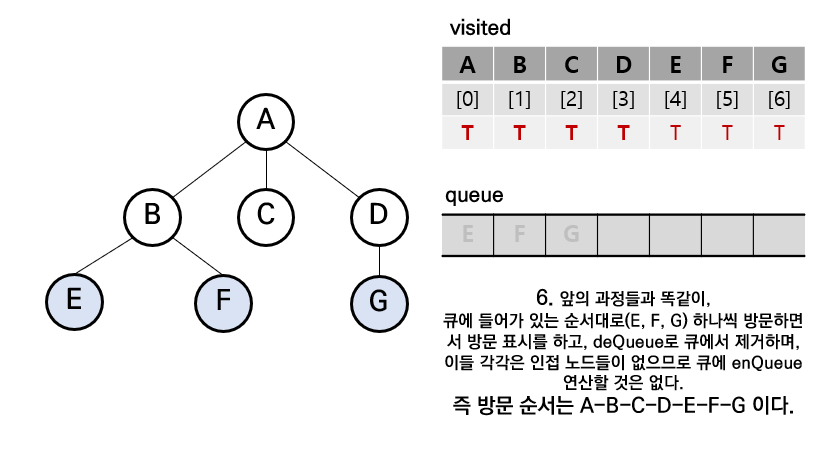
step6.큐에 남아있는 요소들을 차례대로 위와 같은 방법으로 방문 및 표시하면서 결과적으로 BFS 탐색 완료(큐가 완전히 비게 될 때)
1.3 코드
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int number = 9;
int visit[9];
vector<int> a[10];
void bfs(int start) {
queue<int> q;
q.push(start);
visit[start] = true;
while (!q.empty()) {
//큐에 값이 있을 경우 계속 반복 실행
//큐에 값이 있다 -> 아직 방문하지 않은 노드가 존재한다.
int x = q.front();
q.pop();
printf("%d ", x);
for (int i = 0; i < a[x].size(); i++) {
int y = a[x][i];
if (!visit[y]) {
q.push(y);
visit[y] = true;
}
}
}
}
int main(void) {
//1과 2를 연결
a[1].push_back(2);
a[2].push_back(1);
//1과 3을 연결
a[1].push_back(3);
a[2].push_back(1);
//2과 4를 연결
a[2].push_back(4);
a[4].push_back(2);
//2과 5를 연결
a[2].push_back(5);
a[5].push_back(2);
//4와 8을 연결
a[4].push_back(8);
a[8].push_back(4);
//5와 9를 연결
a[5].push_back(9);
a[9].push_back(5);
//3과 6을 연결
a[3].push_back(6);
a[6].push_back(3);
//3과 7을 연결
a[3].push_back(7);
a[7].push_back(3);
bfs(1);
return 0;
}
[출력 결과]

2. DFS
2.1 개념
깊이 우선 탐색(Depth First Search)는 한 방향으로 끝까지 가고 나서 답을 확인하는 과정이다. DFS 알고리즘은 어떠한 선택을 하건 잘 동작하며, 누구를 우선 선택할 것인지에 대한 기준은 구현하는 이가 결정해도 되는 문제이다. DFS의 핵심에는 세 가지가 있다. 하나에게만 연락을 하고, 연락할 사람이 없으면 자신에게 연락한 사람에게 이를 알린다. 마지막으로 처음 연락을 시작한 사람의 위치에서 연락은 끝이 난다.
·장점
·현재 경로상의 노드들만 기억하면 되므로 저장 공간의 수요가 비교적 작다.
·목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.
·단점
·해가 없는 경로에 깊이 빠질 가능성이 있다.
·얻어진 해가 최단 경로가 된다는 보장이 없다.2.2 방법
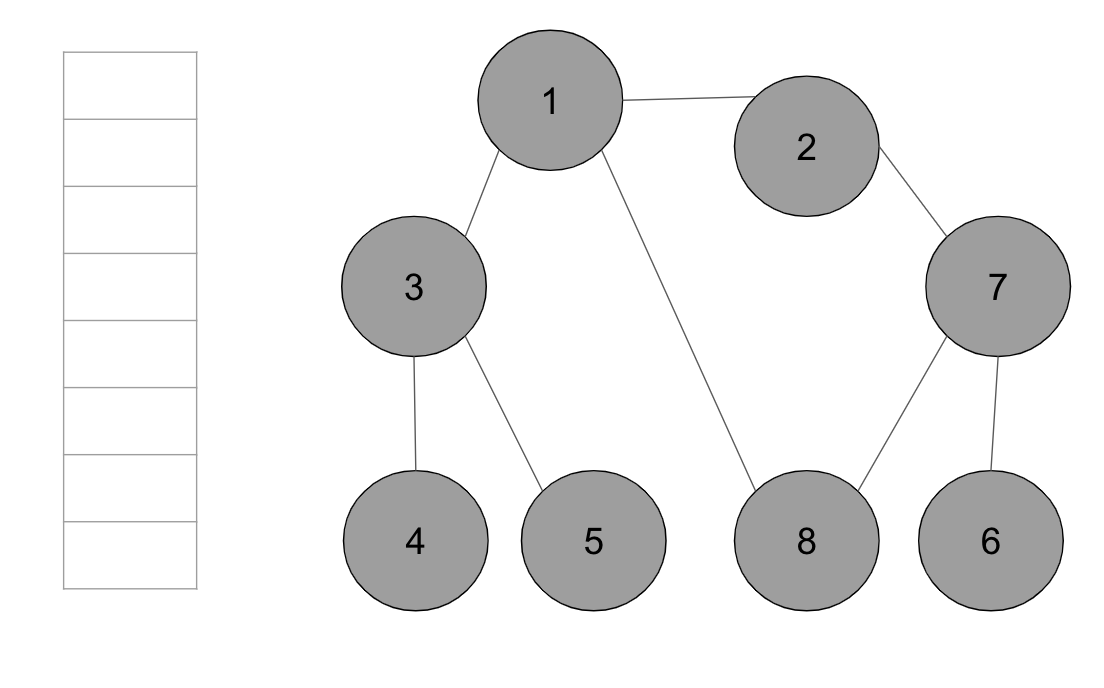
ex) 그래프의 노드 1을 시작 노드로 설정하여 DFS를 이용하여 탐색한다고 가정
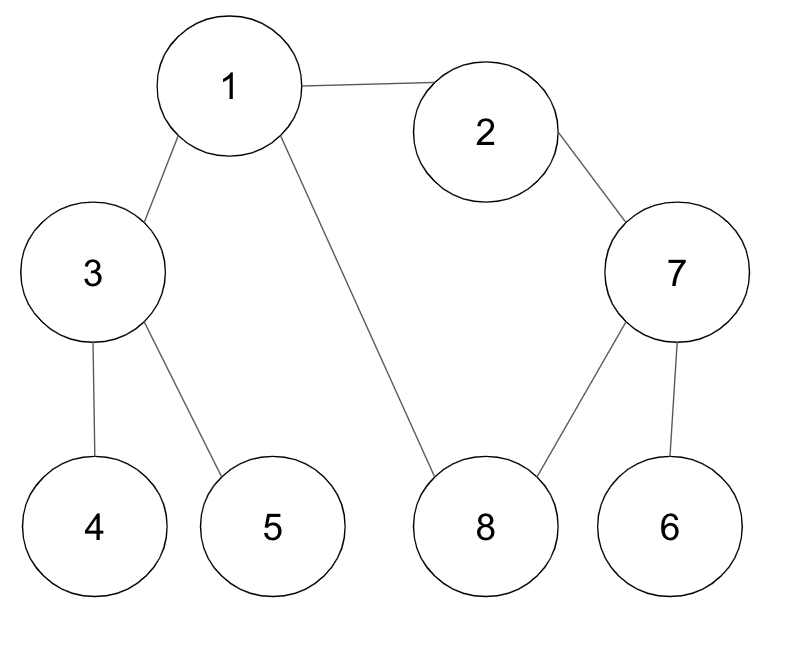
인접한 노드 중에서 방문하지 않은 노드가 있으면 번호가 낮은 순서부터 처리한다. (방문 처리된 노드는 회색, 현재 처리하는 스택의 최상단 노드는 하늘색)
step1. 시작 노드 1을 스택에 삽입하고 방문 처리
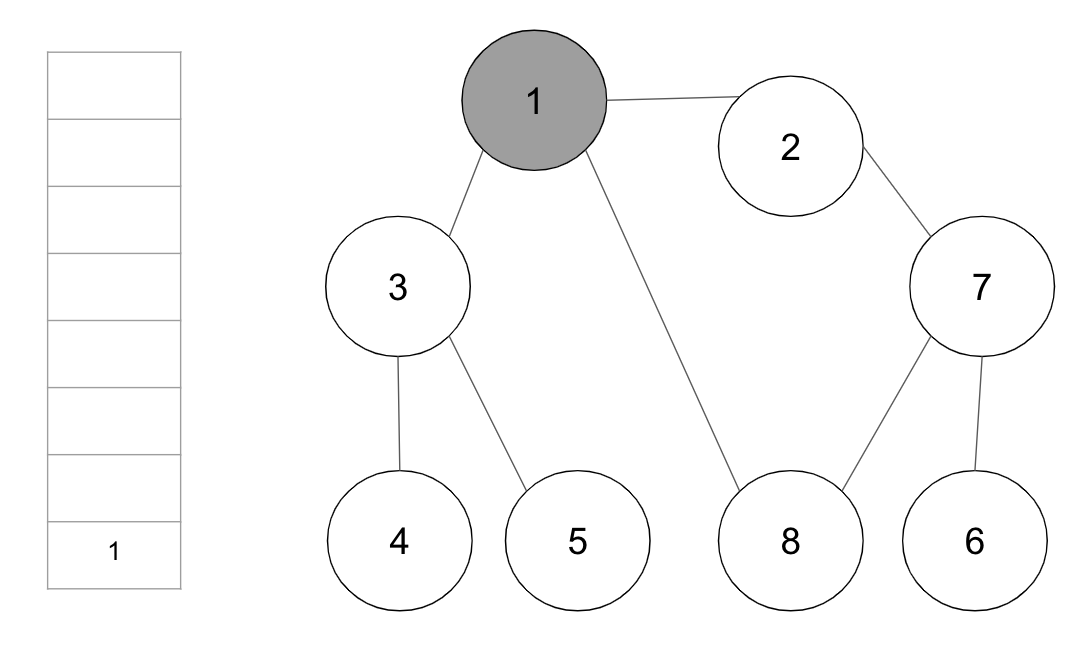
step2. 스택의 최상단 노드 1에 방문하지 않은 인접 노드 2, 3, 7 중에서 가장 작은 노드 2를 스택에 넣고 방문 처리
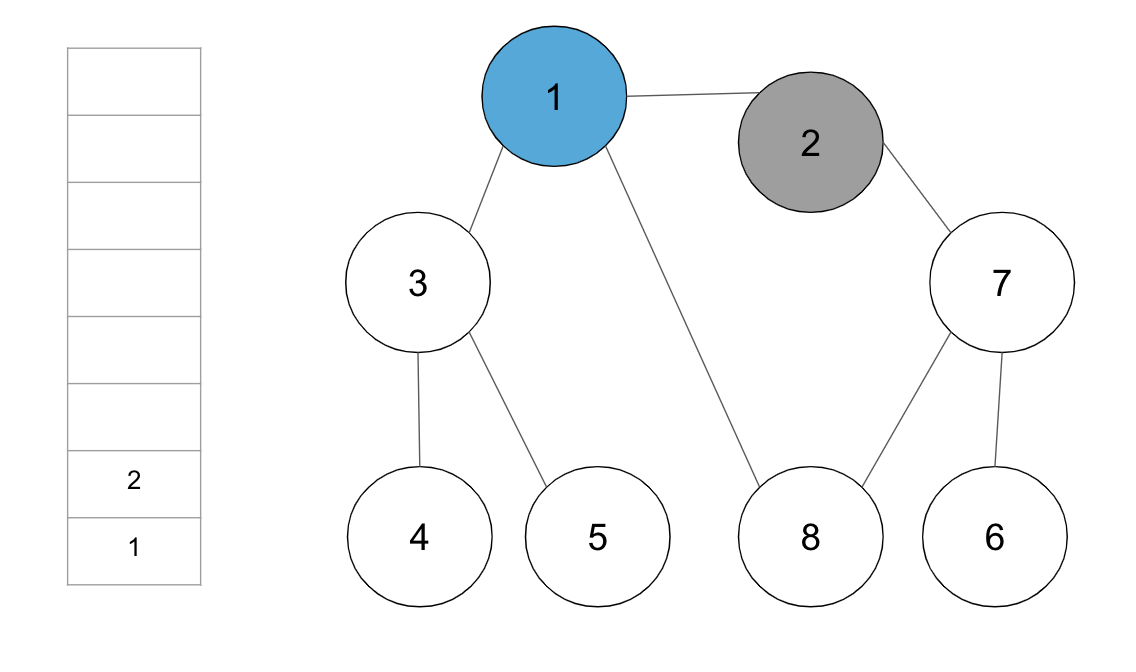
step3. 스택의 최상단 노드 2에 방문하지 않은 인접 노드 7을 스택에 넣고 방문처리
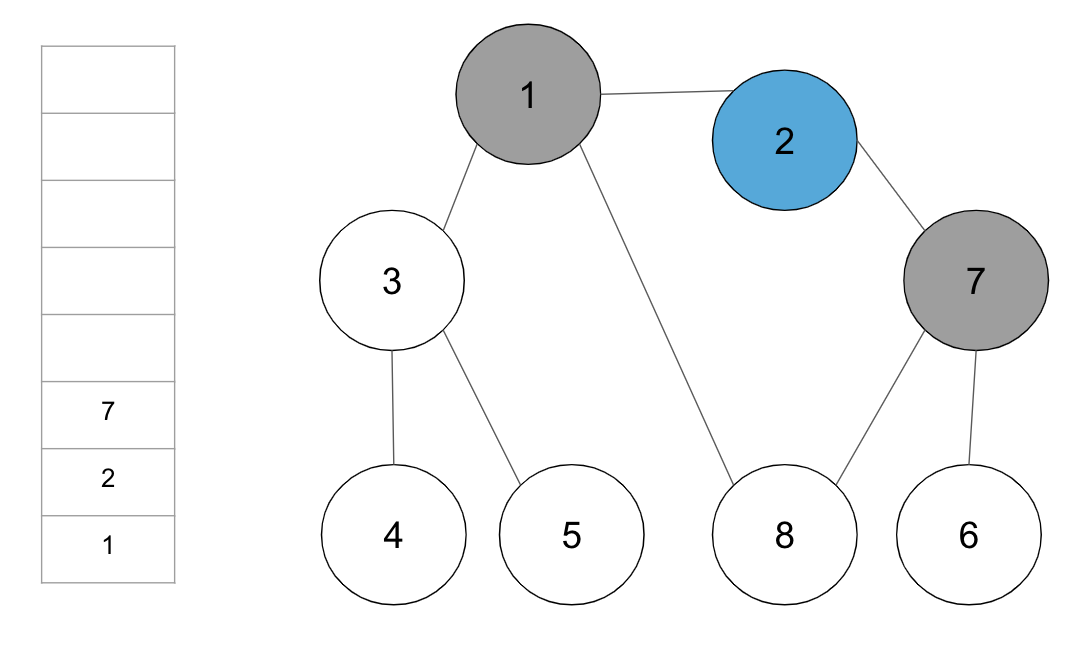
step4. 스택의 최상단 노드 7에 방문하지 않은 인접 노드 6과 8 중에서 가장 작은 노드인 6을 스택에 넣고 방문 처리
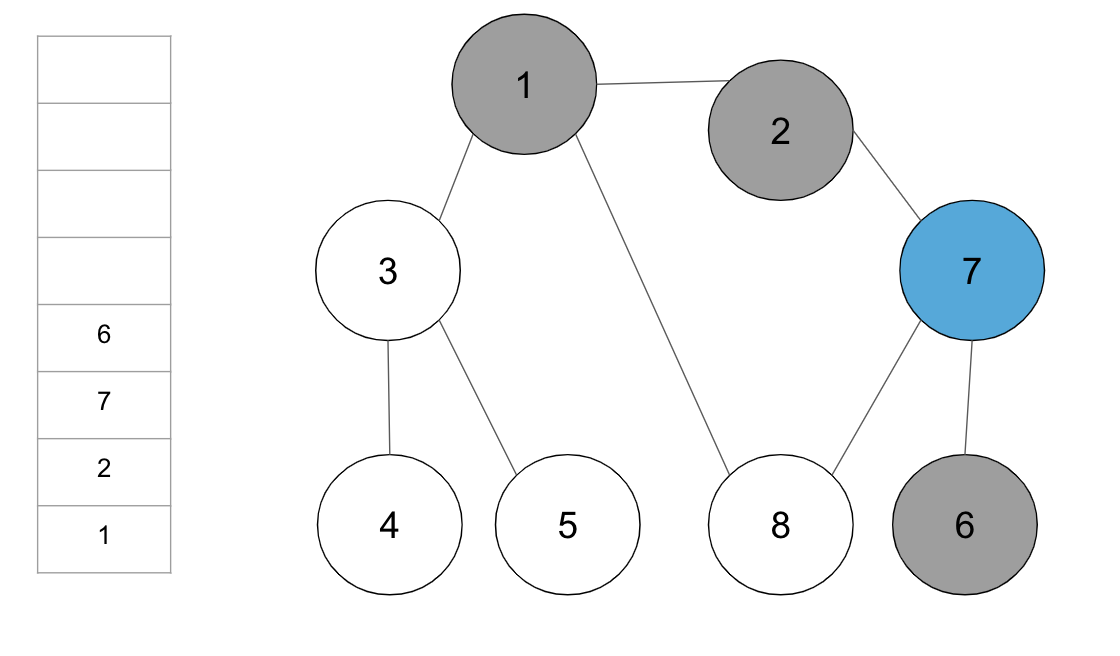
step5. 스택의 최상단 노드 ‘6’에 방문하지 않은 인접 노드가 없으므로, 스택에서 ‘6’번 노드를 꺼냄
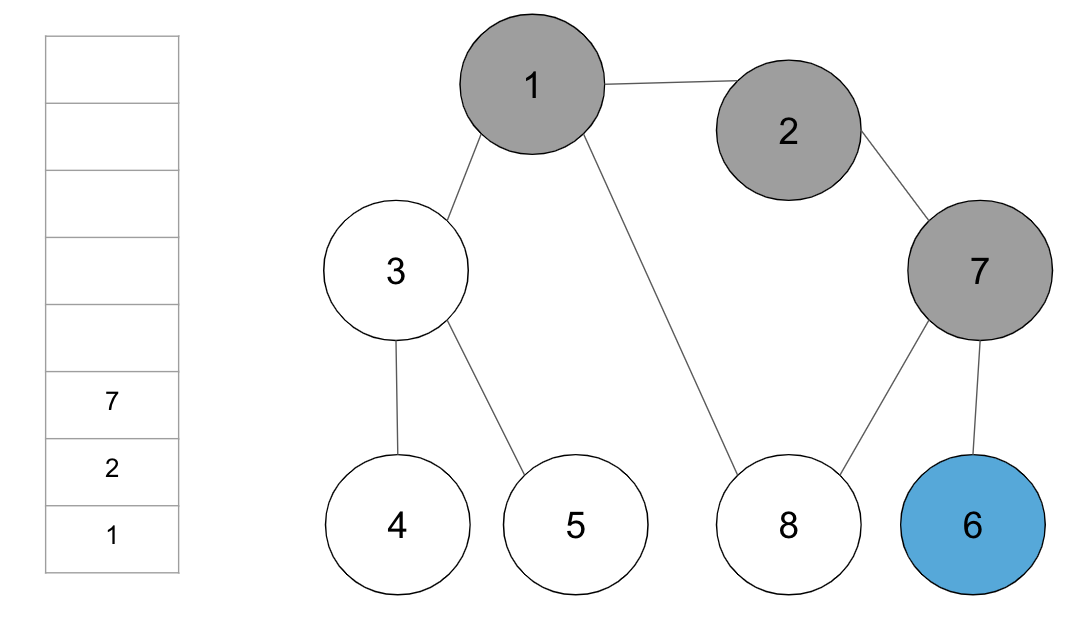
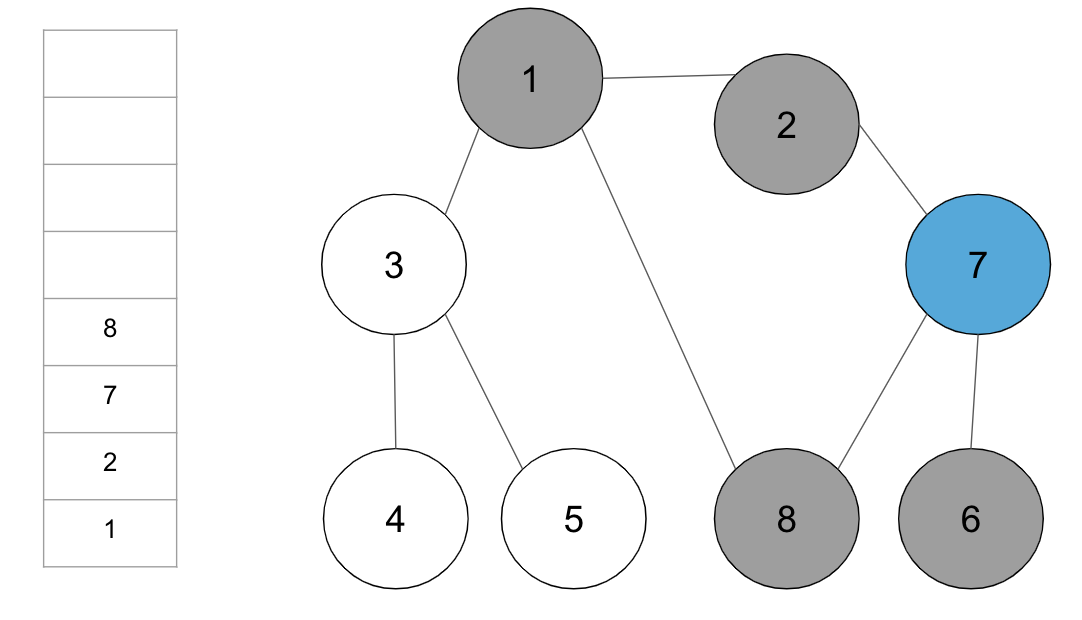
step6. 스택의 최상단 노드 ‘7’에 방문하지 않은 인접 노드 ‘8’이 있으므로, ‘8’번 노드를 스택에 넣고 방문 처리
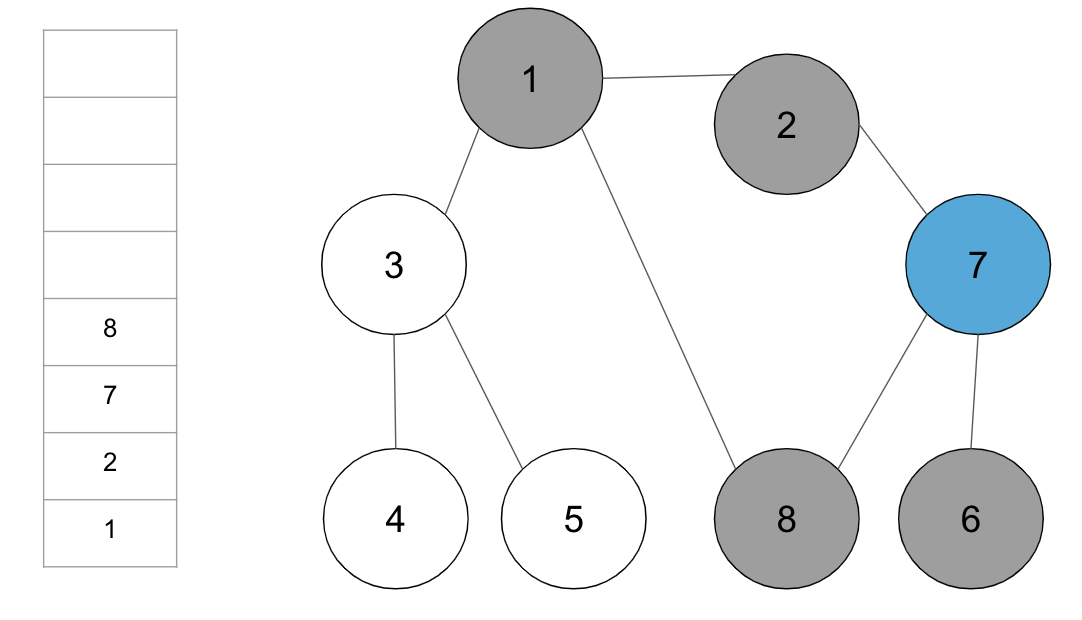
step7. 스택 최상단 노드 ‘8’에 방문하지 않은 인접 노드가 없으므로, 스택에서 ‘8’번 노드를 꺼냄
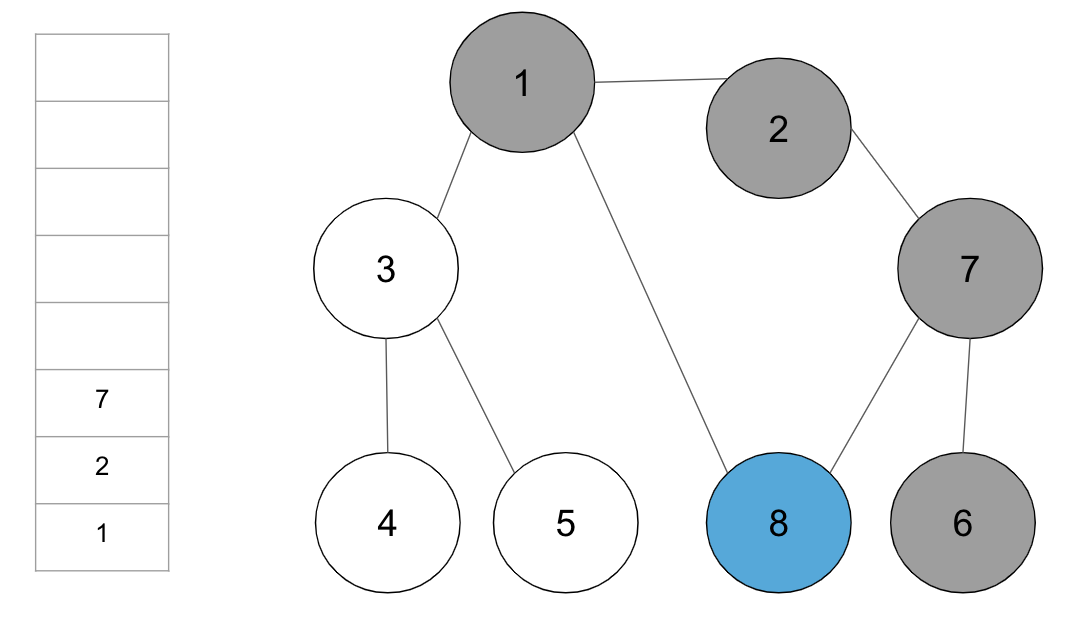
step8. 스택의 최상단 노드 ‘7’에 방문하지 않은 인접 노드가 없으므로, 스택에서 ‘7’번 노드를 꺼냄
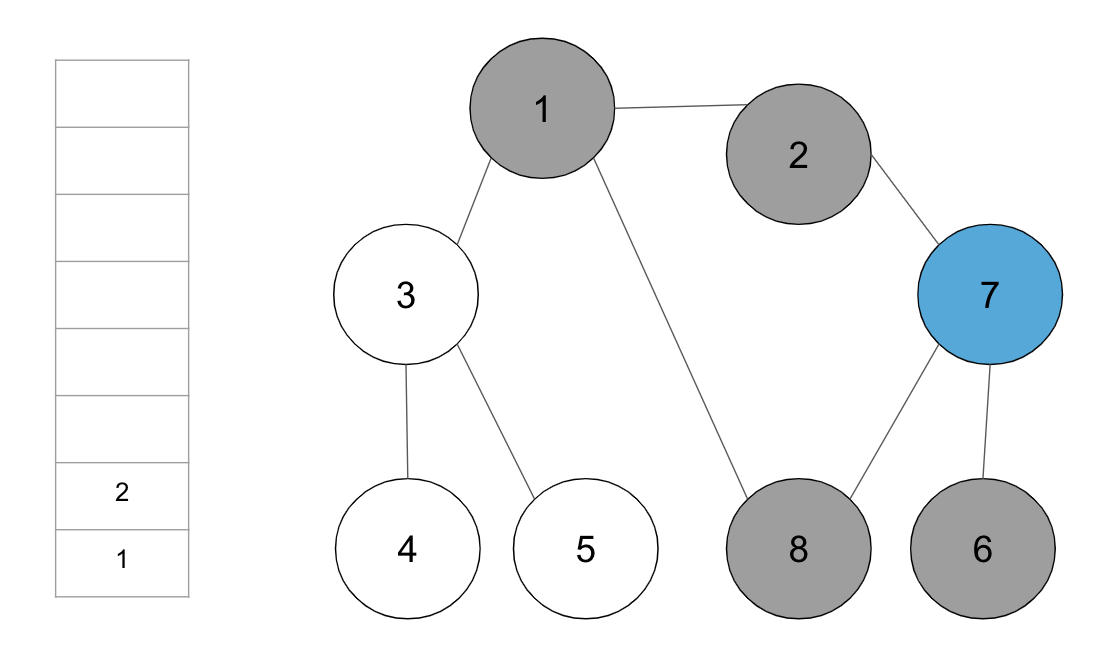
step9. 스택의 최상단 노드 ‘2’에 방문하지 않은 인접 노드가 없으므로, 스택에서 ‘2’번 노드를 꺼냄
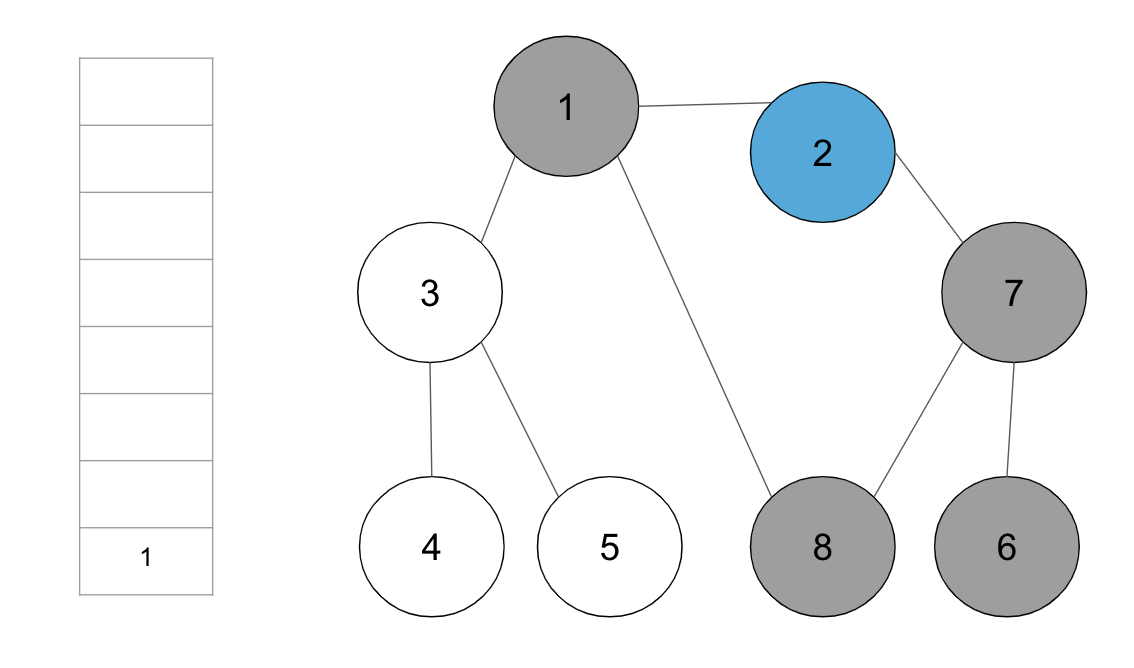
step10. 스택의 최상단 노드 ‘1’에 방문하지 않은 인접 노드 ‘3’을 스택에 넣고 방문 처리
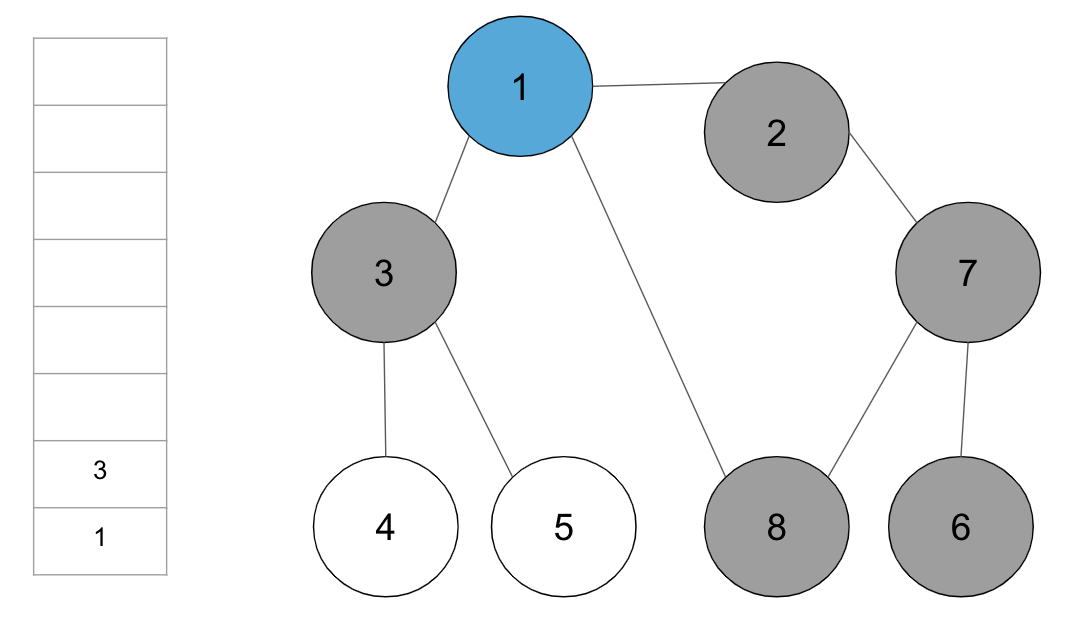
step11. 스택의 최상단 노드 ‘3’에 방문하지 않은 인접 노드 ‘4’, ‘5’ 중 가장 작은 노드 ‘4’를 스택에 넣고 방문 처리
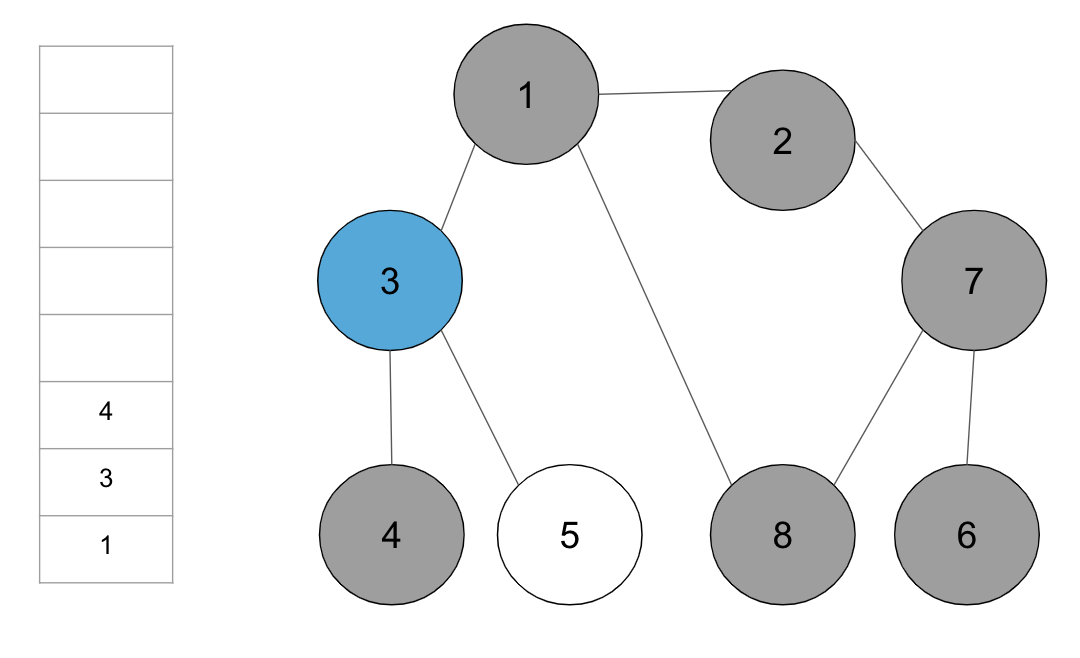
step12. 스택의 최상단 노드 ‘4’에 방문하지 않은 인접 노드 ‘5’가 있으므로, ‘5’번 노드를 스택에 넣고 방문 처리
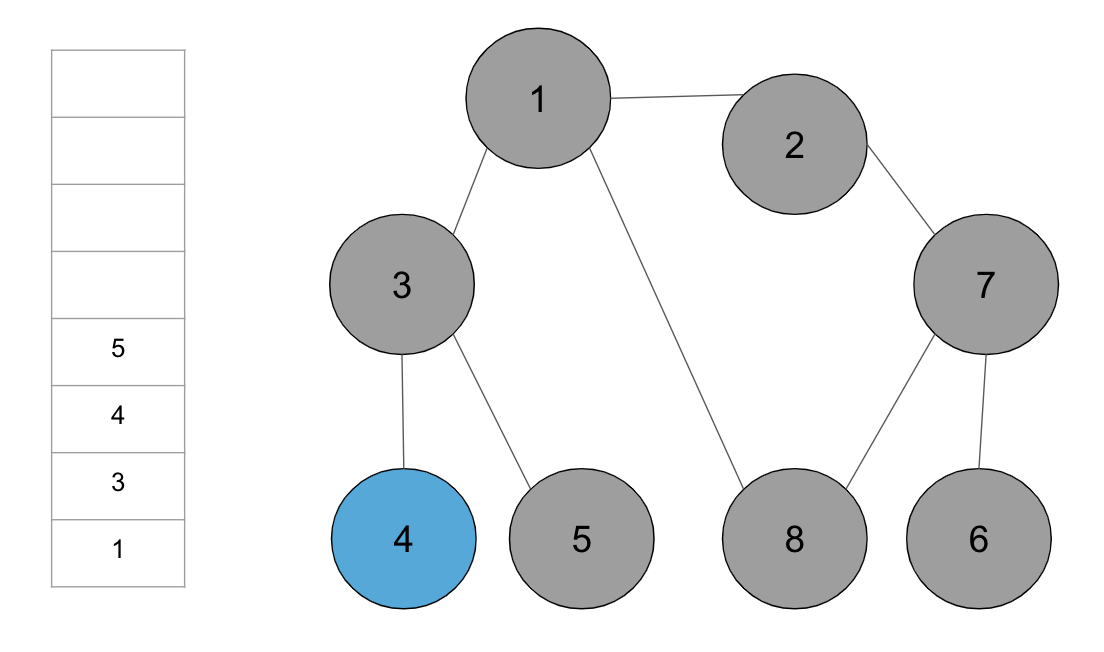
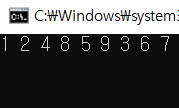
step13. 남아 있는 노드에 방문하지 않은 인접 노드가 없다. 따라서 모든 노드를 차례대로 꺼내면 다음과 같다. 방문 순서는 1>2>7>6>8>3>4>5이다.
2.3 코드
#include <iostream>
#include <vector>
using namespace std;
int number = 9;
int visit[9];
vector<int> a[10];
void dfs(int start) {
if (visit[start]) {
//방문한 경우 바로 빠져나옴
return;
}
visit[start] = true;
printf("%d ", start);
for (int i = 0; i < a[start].size(); i++) {
int x = a[start][i];
dfs(x);
}
}
int main(void) {
//1과 2를 연결
a[1].push_back(2);
a[2].push_back(1);
//1과 3을 연결
a[1].push_back(3);
a[2].push_back(1);
//2과 4를 연결
a[2].push_back(4);
a[4].push_back(2);
//2과 5를 연결
a[2].push_back(5);
a[5].push_back(2);
//4와 8을 연결
a[4].push_back(8);
a[8].push_back(4);
//5와 9를 연결
a[5].push_back(9);
a[9].push_back(5);
//3과 6을 연결
a[3].push_back(6);
a[6].push_back(3);
//3과 7을 연결
a[3].push_back(7);
a[7].push_back(3);
dfs(1);
return 0;
}[출력 결과]
3. BFS와 DFS의 차이점
가장 큰 차이점은 탐색하는 방향과 사용하는 자료구조가 다르다는 점이다. BFS는 큐 자료구조를 사용한다. 인접한 노드를 반복적으로 큐에 넣도록 하여 자연스럽게 먼저 들어온 것이 먼저 나가게 되는 FIFO가 되어 가까운 노드부터 탐색을 진행할 수 있다. DFS는 스택을 사용한다. 또한, 구조적으로 함수를 호출할 때 스택의 원리를 이용하기 때문에 스택을 선언하여 사용하지 않는 재귀적 함수 호출로 구현할 수 있다.
4. BFS 관련 문제 풀이
4.1 문제 설명
이진 직사각형 행렬 형태의 미로가 주어지며 미로에서 주어진 소스에서 주어진 목적지까지의 최단 경로의 길이를 찾는다. 경로는 값이 1인 셀로만 구성될 수 있으며 네 방향 중 하나로 한 단계만 이동할 수 있다.
예시를 들자면 소스가 (0,0)이고 경로가 (7,5)이면 최단 경로의 길이는 12이다.
[ 1 1 1 1 1 0 0 1 1 1 ]
[ 0 1 1 1 1 1 0 1 0 1 ]
[ 0 0 1 0 1 1 1 0 0 1 ]
[ 1 0 1 1 1 0 1 1 0 1 ]
[ 0 0 0 1 0 0 0 1 0 1 ]
[ 1 0 1 1 1 0 0 1 1 0 ]
[ 0 0 0 0 1 0 0 1 0 1 ]
[ 0 1 1 1 1 1 1 1 0 0 ]
[ 1 1 1 1 1 0 0 1 1 1 ]
[ 0 0 1 0 0 1 1 0 0 1 ]4.2 코드
#include <iostream>
#include <queue>
#include <vector>
#include <climits>
#include <cstring>
using namespace std;
struct Node
{
int x, y, dist;
};
int row[] = { -1, 0, 0, 1 };
int col[] = { 0, -1, 1, 0 };
bool isValid(vector<vector<int>> const& mat, vector<vector<bool>>& visited,
int row, int col) {
return (row >= 0 && row < mat.size()) && (col >= 0 && col < mat[0].size())
&& mat[row][col] && !visited[row][col];
}
int findShortestPathLength(vector<vector<int>> const& mat, pair<int, int>& src,
pair<int, int>& dest)
{
if (mat.size() == 0 || mat[src.first][src.second] == 0 ||
mat[dest.first][dest.second] == 0) {
return -1;
}
int M = mat.size();
int N = mat[0].size();
vector<vector<bool>> visited;
visited.resize(M, vector<bool>(N));
queue<Node> q;
int i = src.first;
int j = src.second;
visited[i][j] = true;
q.push({ i, j, 0 });
int min_dist = INT_MAX;
while (!q.empty())
{
Node node = q.front();
q.pop();
int i = node.x, j = node.y, dist = node.dist;
if (i == dest.first && j == dest.second)
{
min_dist = dist;
break;
}
for (int k = 0; k < 4; k++)
{
if (isValid(mat, visited, i + row[k], j + col[k]))
{
visited[i + row[k]][j + col[k]] = true;
q.push({ i + row[k], j + col[k], dist + 1 });
}
}
}
if (min_dist != INT_MAX) {
return min_dist;
}
return -1;
}
int main()
{
vector<vector<int>> mat =
{
{ 1, 1, 1, 1, 1, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 1, 1, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 1, 1, 1, 0, 0, 1 },
{ 1, 0, 1, 1, 1, 0, 1, 1, 0, 1 },
{ 0, 0, 0, 1, 0, 0, 0, 1, 0, 1 },
{ 1, 0, 1, 1, 1, 0, 0, 1, 1, 0 },
{ 0, 0, 0, 0, 1, 0, 0, 1, 0, 1 },
{ 0, 1, 1, 1, 1, 1, 1, 1, 0, 0 },
{ 1, 1, 1, 1, 1, 0, 0, 1, 1, 1 },
{ 0, 0, 1, 0, 0, 1, 1, 0, 0, 1 },
};
pair<int, int> src = make_pair(0, 0);
pair<int, int> dest = make_pair(7, 5);
int min_dist = findShortestPathLength(mat, src, dest);
if (min_dist != -1)
{
cout << "소스에서 목적지까지의 최단 경로의 길이는 " << min_dist << endl;
}
else {
cout << "지정된 소스에서 대상에 연결할 수 없습니다.";
}
return 0;
}[출력 결과]

