HW12

1. 그래프 표현 방법

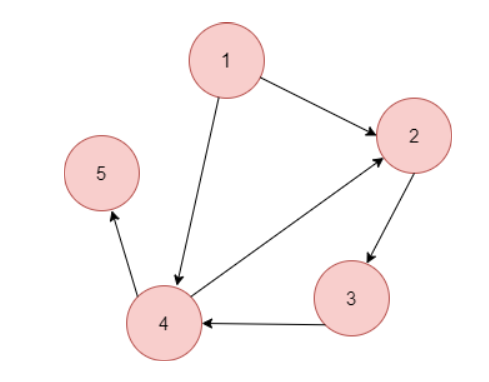
이 그래프를 인접 리스트로 표현하고 싶다면 하단의 코드처럼 작성하면 된다.

vector<int> w[6]; //인덱스 0은 사용 안 함
w[1].push_back(2); //1에서 2로 향하는 이음선
w[1].push_back(4); //1에서 4로 향하는 이음선
w[2].push_back(3); //2에서 3로 향하는 이음선
w[3].push_back(4); //3에서 4로 향하는 이음선
w[4].push_back(2); //4에서 2로 향하는 이음선
w[4].push_back(5); //4에서 5로 향하는 이음선

정점 1과 연결되어있는 모든 정점을 출력하고 싶다면

for (int v : w[1]) {
	cout << v << endl;
}

벡터(vector)를 이용하면 포인터를 사용할 필요 없이 인접리스트를 쉽게 구현할 수 있다.

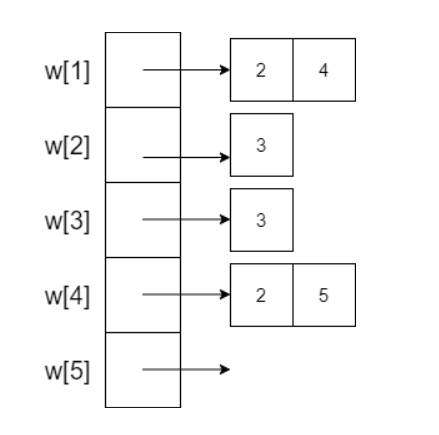
[그래프 표현방법 코드]

#include <iostream>
#include <vector>
using namespace std;

int main() {
	vector<int> w[6]; //인덱스 0은 사용하지 않는다
	w[1].push_back(2); //1에서 2로 향하는 선
	w[1].push_back(4); //1에서 4로 향하는 선
	w[2].push_back(3); //2에서 3로 향하는 선
	w[3].push_back(4); //3에서 4로 향하는 선
	w[4].push_back(5); //4에서 5로 향하는 선
	for (int v : w[1]) {
		cout << v << endl;
	}
	return 0;
}

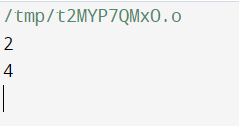
[출력 결과]
for문에서 w[1]에 인접한 정점을 출력하는 것 결과가 되기 때문에 1에 인접한 정점인 2와 4가 출력되는 것을 볼 수 있다.

2. 다익스트라 알고리즘

2.1 다익스트라 알고리즘이란?

다익스트라 알고리즘(Dijkstra algorithm)은 최단 경로 알고리즘이며 하나의 시작 정점 v에서 모든 다른 정점까지의 최단 경로를 찾는 알고리즘이다. 그래프의 방향의 유무는 상관이 없지만 그패프의 어느 간선의 가중치라도 음수가 있으면 안된다는 특징을 가지고 있다. 음의 가중치를 가지는 간선이 있고, 가중치 합이 음인 사이클이 존재하지 않은 경우 벨만-포드 알고리즘을 사용하면 된다.

· 다익스트라 알고리즘을 구현하기 위한 과정

1. 출발점으로부터 최단거리를 저장할 배열을 만들고, 출발 노드에는 0을, 다른 노드들에는 큰 값인 INF을 채워 넣는다.
2. 현재 노드를 나타내는 변수 A에 출발 노드의 번호를 저장한다.
3. a로부터 갈 수 있는 임의의 노드 B에 대해 d[A]+p[A][B]와 d[B]의 값을 비교한다. INF와 비교할 때 전자가 작다.
4. 만약 d[A]+p[A][B]의 값이 더 작다면, d[B]의 값으로 갱신시킨다.
5. A의 모든 이웃 노드 B에 대해 이 작업을 수행한다.
6. B의 상태를 '방문 완료'로 바꾼다. A는 더 이상 사용할 수 없다.
7. '미방문' 상태인 모든 노드들 중, 출발점으로부터 거리가 가장 짧은 노드를 골라서 그 노드를 A에 저장한다.
8. 도착 노드가 '방문 완료' 상태가 되거나, 더 이상 미방문 상태의 노드를 선택할 수 없을 때까지, 3에서 7까지의 과정을 반복한다.

> 작업이 끝난 뒤, 도착 노드에 저장된 값이 A로부터의 최단거리이다.

위에서 작성한 과정들을 직접 그림을 통하여 설명하였다.

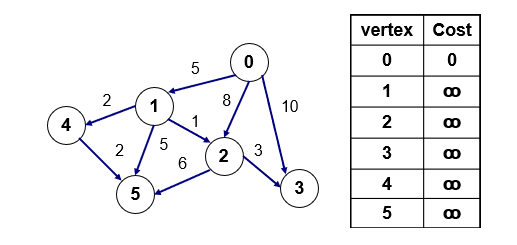
cost는 점을 가기 위한 값을 기록하는 배열이고, 0번을 시작점으로 갈 수 있는 모든 점에 대한 최단 거리를 구한다. 각 점에 대한 거리를 모르기 때문에 무한대로 놓는다. 0번에서 시작하기 때문에 0번 값을 0으로 갱신한다.

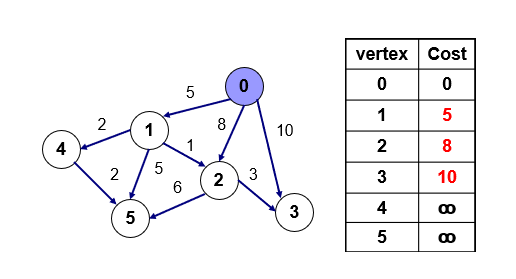
0번을 방문하고 0번 점을 갈 수 있는 방법은 1, 2, 3번 점이 있다. 기존의 cost 배열에 있는 값과 0에서 가는 값을 비교해서 작으면 값을 갱신한다. 무한대였기 때문에 각각의 값인 5, 8, 10으로 갱신한다.

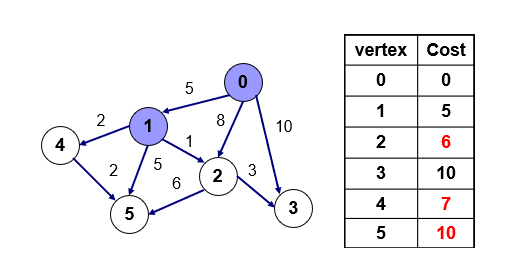
방문하지 않은 점 중에서 값이 가장 작은 점 1번을 방문한다. 1번에서 갈 수 있는 점 2, 4, 5번의 거리는 0번에서 1번으로 가는 거리 5, 그리고 1번에서 갈 수 있는 점의 거리를 더하면 된다. 1번을 통해서 가는 거리가 짧기 때문에 값을 갱신한다.

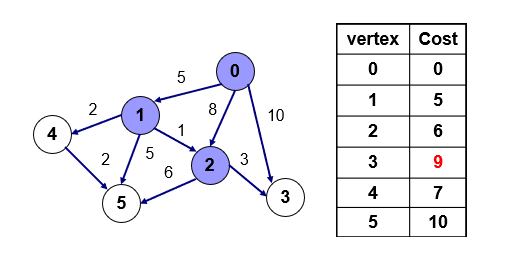
2번을 방문한다. 2번을 통해서 갈 수 있는 3, 5번에서 더 짧은 거리가 3이므로 2에서 3으로 가는 점의 거리인 9로 갱신한다.

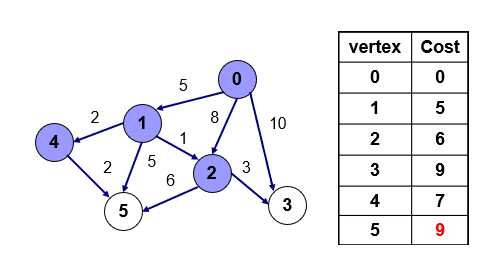
4번을 방문한다. 4번을 통해서 5번으로 가는 값이 위에 나와있는 값인 10보다 작기 때문에 갱신해준다. 4번을 통해서 5번으로 가면 5+2+2=9의 값이 나온다.

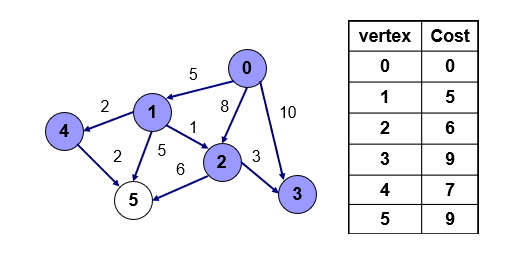
3번을 방문한다. 더 이상 갈 수 있는 점이 없으니 다른 점을 탐색한다.

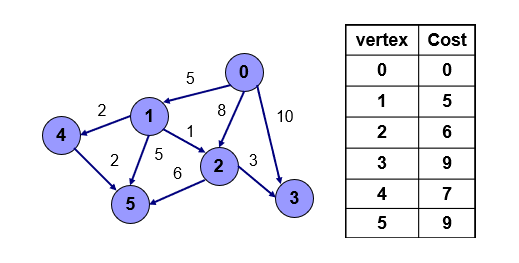
5번을 방문한다. 더 이상 갈 수 있는 점이 없기 때문에 종료한다.

∴ cost 배열이 최단 경로가 된다.

2.2 코드 구현

#include <iostream>
#include <queue>
#include <vector>
#define max 100
#define INF 9999
using namespace std;

vector <pair<int,int>> adj[max]; // 노드들의 정보들을 담는 벡터
int vertex[max]; //최단거리를 저장하는 배열
int V,E;

// dist배열을 초기화 함수
void dist_set(void){
    for(int i = 1;i<=V;i++){vertex[i] = infy;}
}

void dijkstra(int node){
    priority_queue<pair<int,int>> pq; 
    pq.push(make_pair(0,node)); 
    
    while(!pq.empty()){
        node = pq.top().second; 
        pq.pop(); 
        for(int i = 0;i<adj[node].size();i++){
            int next_node = adj[node][i].first; 
            int new_val = adj[node][i].second + vertex[node]; 
            int before_val = vertex[next_node];
            if(new_val < before_val){ 
                vertex[next_node] = new_val;
                pq.push(make_pair(-1*new_val,next_node)); 
            }
        }
    }
}
int main(void){
    cin >> V >> E; //V는 정점의 갯수, E는 간선의 갯수
    for(int i=0;i<E; i++){
        int u,v,w;
        cin >> u >> v >> w;
        adj[u].push_back(make_pair(v,w)); //adj[노드].<노드,가중치>
    }
    vertex_set(); //dist배열 초기화
    vertex[1] = 0; //시작점 초기화
    dijkstra(1);
    for(int i =1 ;i<=V;i++){cout << vertex[i] << " ";}
}

3. 백준 문제 풀이 (옵션)

3.1 1753 최단경로

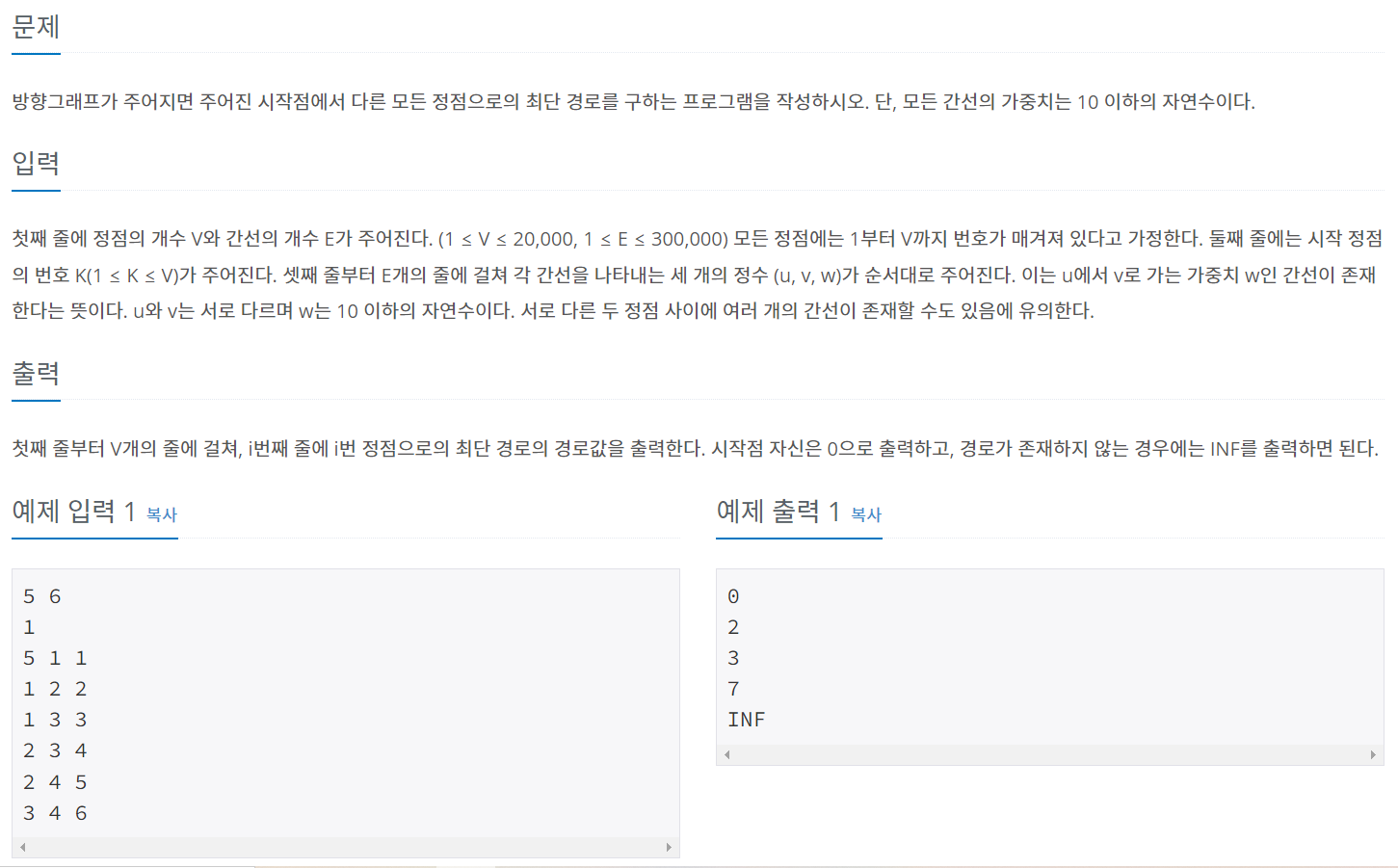
[코드]

#include <cstdio>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;

int vertex[20001];
vector<vector<pair<int, int>>> way;

int main(void){
    int v, e, k;
    int city_a, city_b;
    int here, cost;
    int there, nextCost;

    priority_queue<pair<int ,int>> pq;
    
    scanf("%d %d", &v, &e);
    scanf("%d", &k);
    way.resize(v+1);
    for(int i=0; i<e; i++){
        scanf("%d %d %d", &city_a, &city_b, &cost);
        way[city_a].push_back(make_pair(city_b, cost));
    }
    
    for(int i=1; i<=v; i++){
        vertex[i] = -1;
    }
    
    vertex[k] = 0;
    pq.push(make_pair(0, k));

    while(!pq.empty()){
        cost = -1 * pq.top().first;
        here = pq.top().second;
        pq.pop();
        
        if(vertex[here] < cost)
            continue;
        
        for(int i=0; i<way[here].size(); i++){
            
            there = way[here][i].first;
            nextCost = cost + way[here][i].second;
            
            if(vertex[there]==-1){
                vertex[there] = nextCost;
                pq.push(make_pair(-nextCost, there));

            }
            else if(nextCost < vertex[there]){
                vertex[there] = nextCost;
                pq.push(make_pair(-nextCost, there));
            }
            
        }
    }
    for(int i=1; i<=v; i++){
        if(vertex[i] == -1)
            printf("INF\n");
        else
            printf("%d\n", vertex[i]);
    }
    
}

4. BFS 관련 문제 풀이 (옵션)