1. 완전탐색 알고리즘
완전탐색은 간단하게 말해 가능한 모든 경우의 수를 다 확인하여 정답을 찾는 방법이다. 무식하게 정답을 찾는다고 하여 Brute force라고도 부르며, 직관적이어서 이해하기 쉽고 문제의 정확한 결괏값을 얻어낼 수 있는 가장 확실하면서도 기초적인 방법이다.
예를 들어 4자리 정수로 이루어진 암호를 맞춘다고 생각해 보자. 암호를 찾는 가장 확실한 방법은 0000부터 9999까지 10,000개의 경우의 수를 모두 시도해보는 것이다.
다만 computers science에서 문제 해결 알고리즘을 사용할 때는 기본적으로 2가지 규칙을 적용한다.
- 사용된 알고리즘이 적절한가(문제를 해결할 수 있는가)?
- 효율적으로 동작하는가?
상기 2가지 규칙을 생각하면, 완전 탐색은 1번은 확실하게 만족시킬 수 있겠지만 2번 규칙은 확신하기가 어렵다. 그리고 보통은 이 2번 규칙으로 인해 완전 탐색의 사용에 제약이 발생한다.
2. 완전탐색 기법의 활용 방법
완전탐색 기법을 사용하기 위해서는 다음의 사항을 먼저 고려해야 한다.
- 해결하고자 하는 문제의 가능한 경우의 수를 대략적으로 계산한다.
- 가능한 모든 방법을 고려한다.
- 실제로 답을 구할 수 있는지 적용한다.
이때, 2에서 이야기하는 '모든 방법'에는 다음과 같은 다섯 가지 방법이 있다.
- Brute force 기법 : 반복과 조건문을 활용해 모든 경우의 수를 확인하는 방법
- 순열(Permutation) : n개의 원소 중 r개의 원소를 중복 허용 없이 나열하는 방법
- 재귀 호출
- 비트 마스크 : 2진수 표현 기법을 활용하는 방법
- BFS, DFS를 활용하는 방법
3. 완전탐색의 방식에 대한 세부 설명
Brute force 기법
방법과 조건문을 활용해 가능한 모든 방법을 단순하게 확인하는 방법을 말한다. 아주 기초적인 방법이며, 코딩 테스트에서는 거의 출제되지 않는다.
순열(Permutation)
우선 순열이 무엇인지 이해할 필요가 있다. 순열은 '임의의 수열이 있을 때 그것을 다른 순서로 연산하는 방법'을 의미한다. 즉, 순서가 중요하다. 만약 수열에서 숫자 [1, 2, 3]이 있다면 이것을 [1, 2, 3]으로 보는 순서와 [3, 2, 1]로 보는 순서가 차이가 있다는 것이 중요한 경우를 의미하는 것이다.
N개의 서로 다른 데이터를 순열로 나타낸다고 생각해 보자. 그렇다면 전체 순열의 가짓수는 N!개가 된다. [1, 2, 3]을 사전 순으로 나열하는 순열을 생각해보면 쉽게 이해할 수 있다.
[1, 2, 3] → [1, 3, 2] → [2, 1, 3] → [2, 3, 1] → [3, 1, 2] → [3, 2, 1]
순열은 완전탐색의 대표적인 유형이며, 재귀 함수를 이용하거나 파이썬의 경우 itertools라는 라이브러리의 permutations() 메서드를 이용할 수 있다.
재귀 호출
재귀는 말 그대로 자기 자신을 호출하는 것이다. 왜 그렇게 하는 것일까? 예를 들어 총 4개의 숫자 중 2개를 선택하는 경우를 모두 출력한다고 가정해 보자. 1~4까지의 숫자 중 2개를 중복 없이 선택하는 모든 경우의 수를 출력하는 것이다. 이를 반복문으로 표현하려면 다음과 같을 것이다.
for i in range(1, 5):
for j in range(i+1, 5):
print(i, j)그런데 1~4에서 2개가 아니라, N개의 숫자 중 M개를 고르라고 할 때 N과 M이 매우 큰 수라면? 반복문을 수십, 수백 개를 써야 할 것이다.
이때 재귀 함수를 활용하면 자기 자신을 호출함으로써 다음 수를 선택하도록 이동시켜 코드를 매우 짧게 만들 수 있다.
재귀를 사용할 때는 몇 가지 중요한 점이 있다.
- 재귀를 탈출하기 위한 탈출 조건을 반드시 입력할 것
- 현재 함수의 상태를 저장하는 parameter를 넣을 것
- return을 신경 쓸 것
비트 마스크
2진수를 이용하는 컴퓨터의 연산을 이용하는 방식으로, 문제에서 나올 수 있는 모든 경우의 수가 '각 원소가 포함되거나 포함되지 않는 두 가지 선택으로 구성되는 경우' 유용하게 사용할 수 있다.
예컨대 0~9까지의 정수로 이루어진 집합이 있고, 그중 하나의 부분집합 A = {1, 3, 4, 5, 9}가 있다고 하자. 여기서 각 숫자가 부분집합 A에 존재하느냐 아니냐를 1과 0으로 표시할 수 있으며, 이를 표로 표현하면 다음과 같다.
| 숫자 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 비트 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
그리고 상기 표의 '비트'를 하나의 이진수로 간주하면 1000110010_(2)가 되고, 이를 다시 십진수로 변환하면 570이 된다. 따라서 부분집합 A는 570이라는 하나의 수로 표현할 수 있는 것이다.
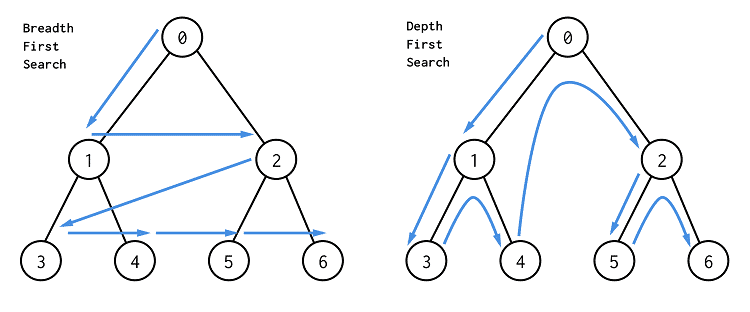
BFS, DFS를 활용하는 방법
그래프 자료 구조에서 모든 정점을 탐색하기 위한 방법이다.
- BFS(Breadth First Search)
너비 우선 탐색으로 현재 정점과 인접한 정점을 우선으로 탐색한다. - DFS(Depth First Search)
깊이 우선 탐색으로, 현재 인접한 정점을 탐색하고 그 다음 안접한 정점을 탐색하여 끝까지 탐색하는 방식이다.