해시 테이블(Hash table)
해시 테이블은 흔히 해시라고도 불리며, 저장 또는 검색 등에서 자주 사용되는 자료 구조로, 간단하게는 {key: value}의 형태로 데이터를 저장하는 자료 구조이다. 데이터의 검색이나 저장이 빨라 자주 사용되는 자료 구조 중 하나이다.
사실 엄밀히 말하자면 해시는 '입력 데이터인 키(key)가 해시 함수(hash function)에 의해 변환된 일정한 길이의 출력 데이터'를 말하는 것이다. 이처럼 해시 테이블을 구성하는 몇 가지 요소가 있는데, 먼저 그것부터 알아보자.
해시 테이블의 구성 요소
키(Key)
- 해시 함수의 입력(Input)이 되는 고유한 데이터
- 키의 길이는 고정되어 있지 않으며, 키를 그대로 저장소의 index로 사용할 경우 이를 위한 저장소 공간이 별도로 필요하다(따라서 저장소 공간의 낭비가 발생한다).
해시 함수(Hash function)
- 키를 입력으로 받아 일정한 길이의 데이터로 반환하는 기능을 하는 함수
- 어떤 알고리즘을 사용하느냐에 따라 출력의 형태가 다양하며, 따라서 암호화에도 해시 함수가 자주 사용된다.
해시(Hash)
- 입력된 키가 해시 함수에 의해 변환된 일정한 길이의 데이터
- 변환된 해시는 데이터의 저장, 조회 등에 활용된다.
값(value)
- 저장소에 최종적으로 저장되는 값
- 해시와 매칭되어 저장된다.
해시 테이블(Hash table)
- 키와 값을 함께 저장한 자료 구조
- 실제 값이 저장되는 장소를 버킷(Bucket) 혹은 슬롯(Slot)이라 한다.
해시 테이블을 사용하는 이유
Direct address table
Direct address table은 키 값을 주소로 사용하는 테이블을 말한다. 만약 (31, 고양이), (560, 강아지)와 같은 데이터가 있다면 '고양이'는 배열의 31번 인덱스에, '강아지'는 배열의 560번 인덱스에 저장하는 것이다. 이러한 자료 구조는 탐색과 삽입, 삭제 등의 연산을 모두 O(1)에 할 수 있지만 다음과 같은 한계점이 있다.
- 최대 키 값에 대해 알고 있어야 한다.
- 최대 키 값이 작아야 실용적으로 사용할 수 있다(최대 키 값이 작을 경우 공간 낭비가 심하다).
Hash table
반면 해시 테이블은 키 값을 해시 함수를 통해 특정 크기의 값으로(여기서 특정 크기는 유저가 결정하여 적절한 해시 함수를 사용 혹은 작성하면 된다) 변환하여 사용하므로 효율적으로 배열을 사용할 수 있다. 예컨대 배열의 크기가 100이라고 할 때 키의 값이 31, 560이라면, 해시 함수를 이용해 키 값을 0~100 사이의 값으로 바꾸어 배열에 저장한다. 이렇게 함으로써 데이터 저장 공간을 훨씬 효율적으로 사용할 수 있다.
충돌(Collision)
어떠한 키 값이 해시 함수를 통과했을 때 출력되는 해시가 같은 값이 될 수도 있다.
입력받은 키 값을 100으로 나눈 나머지를 해시로 출력하는 해시 함수를 사용한다고 하자. 이 경우 키가 1인 데이터와 101인 데이터는 모두 1이라는 해시를 갖게 될 것이다.
이처럼 서로 다른 키 값이 해시 함수를 통과했을 때 그 결과가 중복되는 경우를 충돌(Collision)이라 하며, 충돌을 줄여주는 해시 함수가 좋은 해시 함수가 된다. 충돌이 많아질수록 탐색의 시간복잡도가 O(1)에서 O(n)에 가까워지기 때문이다.
해시 테이블에서는 이러한 충돌 문제를 크게 두 가지 방법으로 해결한다.
분리 연결법(Separate chaining)
분리 연결법은 동일한 버킷의 데이터(즉, 충돌이 발생한 데이터)에 대하여 자료 구조(주로 Linked list와 Tree를 사용하며 충돌한 데이터의 개수에 따라 결정한다)를 활용해 추가 메모리를 사용함으로써 다음 데이터의 주소를 저장하는 것이다.
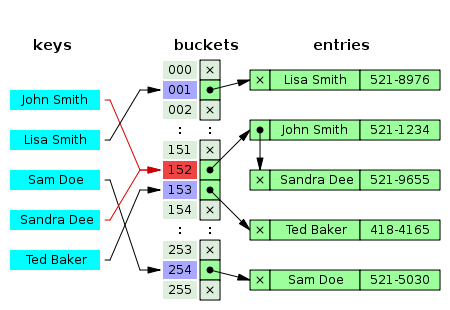
이러한 방식은 해시 테이블의 확장이 필요 없고 구현이 간단하며 삭제 역시 간편하다는 장점이 있다. 그러나 데이터의 수가 많아지면 버킷에 연결되는 데이터가 많아지며, 그에 따라 효율성이 감소한다는 단점이 있다.
개방 주소법(Open addressing)
이 방법은 분리 연결법과 달리 추가적인 메모리를 사용하지 않고, 비어 있는 해시 테이블의 공간을 활용하는 방법이다. 대표적으로 다음의 3가지 방식을 활용하여 구현한다.
- 선형 탐사(Linear probing)
- 현재의 버킷 index로부터 고정폭만큼씩 이동하여 차례대로 검색, 비어 있는 버킷에 데이터를 저장한다.
- 이 경우 특정 해시 값의 주변 버킷이 전부 채워지면서 데이터가 밀집되는 clustering 현상이 발생할 수 있다.
- 제곱 탐사(Quadratic probing)
- 충돌이 발생한 해시를 기준으로 n^2의 폭만큼 건너뛰면서 비어 있는 해시를 찾는 방식
- 선형 탐사에 비해 보다 넓은 기준으로 탐사하므로 탐색 및 삭제가 효율적일 수 있다.
- 초기의 해시 값이 갖다면 제곱 탐사 역시 clustering 문제가 발생할 수 있다.
- 이중 해싱(Double hashing)
- 충돌이 발생할 경우 또 다른 해시 함수를 이용해 해시를 찾는 방식
- 기존의 해시 함수는 최초의 해시 함수를 얻을 때 사용하고, 다른 하나의 해시 함수는 충돌이 발생했을 때 탐사의 폭을 얻기 위해 사용한다.
- 두 번째 해시 함수를 통해 서로 다른 탐사 폭이 나올 확률이 높아 여러 공간에 골고루 저장될 확률도 높아진다(clustering 문제의 해결).
개방 주소법의 경우 별도의 메모리 공간 없이 해시 테이블 내에서 충돌에 대한 처리가 가능해지며, 해시 테이블의 특징인 key-value 간 1:1 매칭 구조가 유지된다는 장점이 있다.
그러나 데이터가 커질수록 버킷 공간 역시 미리 확보해야 하며, 충돌이 많아지면 clustering으로 인해 시간복잡도가 증가하게 된다.
테이블 크기 재할당(Resizing)
해시 테이블은 유한한 공간에 데이터를 담기 위한 구조이며, 따라서 데이터가 증가하다 보면 버킷이 꽉 차 버릴 수 있다. 분리 연결법을 사용한다면 테이블의 빈 공간이 적어질수록 충돌이 많이 발생하면서 linked list의 길이가 길어져 해시 테이블을 사용하는 의미가 없어지고, 개방 주소법을 사용한다면 테이블이 가득 차는 순간 데이터를 저장할 수 없게 될 것이다.
따라서 데이터가 일정 수준으로 증가하게 되면 버킷의 크기를 증가시켜야 하며, 이를 리사이징이라고 한다. 일반적으로 현재의 데이터가 버킷의 75%를 차지하면 리사이징을 실시하며, 0.75를 load factor라고 한다.
참고 자료
- [자료구조] Hash의 개념 및 설명
- [자료구조] 해시(HASH) 알아보기
- [자료구조] 해시테이블이란??
- [자료구조] 해시 테이블 (Hash Table)
- Direct Access Table과 Hash Table
- 자료구조 - Hash Table (해시 테이블)
