완전 이진 트리(complete Binary Tree)
우선 힙에 대해 이해하기 전에 '완전 이진 트리' 자료 구조에 대해 알고 있어야 한다(이진 트리 자체에 대해서는 다음에 다루도록 하자).
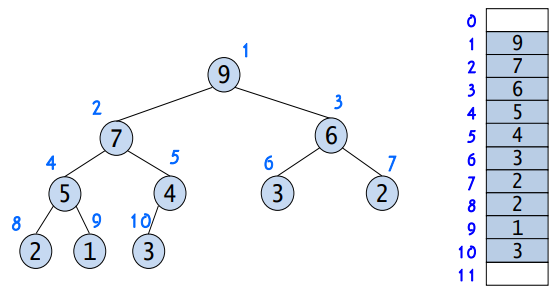
완전 이진 트리란 각 노드가 최대 2개의 자식 노드를 갖는 트리 형태의 자료 구조를 말하는 것으로, 이때 최하단 레벨의 노드는 좌측만 노드가 채워져 있거나 좌측과 우측이 모두 채워져 있어야 하며, 따라서 노드를 삽입할 때는 최하단 좌측 노드부터 차례대로 삽입해야 한다. 아래 예에 나타난 이진 트리 중 5번 트리의 자식 노드도 마찬가지로 왼쪽부터 채워져 있음을 확인할 수 있다.
우선 순위 큐(Qriority queue)
일반적인 큐(Queue)는 먼저 들어오는 데이터가 먼저 나가는 FIFO(First In First Out) 형식의 자료 구조이다. 이와 달리 우선 순위 큐는 먼저 들어오는 데이터가 아니라 큐에 존재하는 데이터 중 '우선 순위'가 높은 데이터가 먼저 나가는 형태의 자료 구조이다.
우선 순위 큐는 따라서 다음과 같은 속성을 지닌다.
- 모든 항목에는 우선 순위가 존재한다.
- 우선 순위가 높은 요소는 우선 순위가 낮은 요소보다 먼저 큐에서 제거된다.
- 우선 순위가 같을 경우에는 큐의 순서에 따라 제거된다.
우선 순위 큐를 구현하는 방법에는 여러 가지가 있지만, 시간 복잡도 측면을 고려할 경우 힙(Heap)의 형태로 구현하는 것이 가장 일반적이다.
| 구현 방법 | enqueue() | dequeue() |
|---|---|---|
| 배열(unsorted array) | O(1) | O(N) |
| 연결 리스트(unsorted linked list) | O(1) | O(N) |
| 정렬된 배열(sorted array) | O(N) | O(1) |
| 정렬된 연결 리스트(sorted linked list) | O(N) | O(1) |
| 힙(heap) | O(logN) | O(logN) |
힙(Heap)
힙의 개요
힙은 이진 힙(Binary heap)이라고도 하며, 우선순위 큐를 위해 고안된 완전 이진 트리 형태의 자료 구조이다. 이는 여러 개의 값 중 최댓값 혹은 최솟값을 찾아내는 연산에서 강점을 보인다.
힙의 종류
힙에는 부모 노드와 자식 노드 간의 관계에 따라 두 가지 종류가 있다.
1. 최대 힙(Max heap)
- 부모의 키 값이 자식 노드의 키 값보다 크거나 같은 힙
(key(부모 노드) ≥ key(자식 노드)) - 가장 큰 값이 루트 노드에 위치함
- 최소 힙(Min heap)
- 부모의 키 값이 자식 노드의 키 값보다 작거나 같은 힙
(key(부모 노드) ≤ key(자식 노드)) - 가장 작은 값이 루트 노드에 위치함
힙의 구현
힙을 구현하는 표준적인 자료 구조는 '배열'이다. 이때 개발 편의를 위해 0번 인덱스는 사용하지 않는다. 트리의 각 노드에 번호를 붙이고, 이 번호를 배열의 인덱스로 간주하면 된다.
완전 이진 트리로서 배열에 빈 공간이 없으므로 부모 혹은 각 자식 노드의 인덱스를 확인하는 연산도 간단히 구현할 수 있다.
- 부모 노드를 구하고자 할 때
부모 노드의 index = 자식 노드의 index / 2 - 자식 노드를 구하조가 할 때
왼쪽 자식 노드의 index = 부모 노드의 index * 2
오른쪽 자식 노드의 index = (부모 노드의 index * 2) + 1
힙의 삽입 연산
힙에 새로운 값을 삽입할 때는 힙 트리의 성질을 만족시키도록 해야 한다.
- 완전이진트리의 마지막 노드에 새로운 노드를 추가한다.
- 추가된 노드를 부모의 노드(해당 노드의 index / 2)와 비교하여 교환한다(최대 힙의 경우 큰 쪽을 부모 노드로, 최소 힙은 작은 쪽을 부모 노드로).
- 정상적인 힙 트리가 될 때까지 2를 반복한다.
힙의 삭제 연산
삭제 연산 역시 힙 트리의 성질을 유지하며 진행해야 한다.
- 삭제하고자 하는 값을 최댓값으로 변경한 후 루트 노드로 이동시킨다.
- 루트 노드를 삭제하고 그 빈 자리에 힙 트리의 마지막 노드를 가져온다.
- 루트 노드 자리에 위치한 새로운 노드를 자식 노드와 비교하여 교환한다.
- 정상적인 힙 트리가 될 때까지 3을 반복한다.
파이썬을 이용한 힙 구현
파이썬은 heapq 모듈을 이용해 힙 구조를 구현할 수 있다. 다만 구조를 알아볼 필요가 있으므로 우선 '최대 힙'을 기준으로 직접 구현해 보자.
Heapify
Heapify는 이진 트리 구조가 힙 속성을 유지하도록 하는 작업을 말한다. 다음 함수는 이진 트리 구조와 노드 위치를 넣었을 때 해당 노드와 자식 노드를 비교하여 최대 힙 구조를 유지하도록 위치를 변경하는 합수이다.
def max_heapify(bt_list, i):
largest = i # 현재 확인할 노드의 값을 최댓값으로 설정하고, 각 자식 노드의 인덱스를 설정한다.
left = 2 * i
right = (2 * i) + 1
if left <= len(bt_list)-1:
if bt_list[left] > bt_list[i]: # 왼쪽 자식 노드와 먼저 비교하여 자식 노드가 크면 최댓값으로 설정한다.
largest = left
if right <= len(bt_list)-1:
if bt_list[right] > bt_list[largest]: # 오른쪽 자식 노드와 비교하여 더 큰 쪽을 최댓값으로 설정한다.
largest = right
if largest != i: # 최댓값이 부모 노드가 아니라면, 즉 자식 노드가 더 크다면 둘을 교환(Swap)한다.
bt_list[i], bt_list[largest] = bt_list[largest], bt_list[i]
max_heapify(bt_list, largest) # 해당 노드에서 다시 자식 노드와 비교하는 작업을 실시한다.
return bt_list이 함수를 사용했을 때 결과를 보면 그 기능을 확인할 수 있다.
bt_list = [None, 5, 7, 13, 15, 30, 25, 4]
heap = max_heapify(bt_list, 3)>>> [None, 5, 7, 25, 15, 30, 13, 4]보다시피 3번 노드에 있던 13과 그 자식 노드 25, 4를 비교하여 25와 13의 위치가 바뀌었음을 확인할 수 있다.
Build heap
이제 앞에서 선언한 heapify 함수를 이용해 완전 이진 트리를 힙 구조로 만드는 작업을 할 수 있다. 힙을 배열 구조로 표현하면 n/2+1부터 n까지는 리프 노드에 해당한다(상기 예에서 노드의 수가 7이므로 4번 노드부터 7번 노드까지는 리프 노드이다). 마지막 리프 노드를 제외한 나머지 노드 중 마지막 노드(n/2)부터 루트 노드(1)까지 차례로 max_heapify를 수행하면 된다.
def build_max_heap(bt_list):
n = (len(bt_list)-1) // 2
for i in range(n, 0, -1):
heap = max_heapify(bt_list, i)
return heap조금 전과 동일한 리스트에 함수를 적용해 보자.
bt_list = [None, 5, 7, 13, 15, 30, 25, 4]
heap = build_max_heap(bt_list)>>> [None, 30, 15, 25, 5, 7, 13, 4]Peak
heap에서 최댓값을 반환하는 기능이다. 최대 힙에서 최댓값은 항상 루트 노드이므로 heap[1]로 구현할 수 있다.
Extract
Extract는 heap에서 최댓값을 '추출'하는 기능이다. 단순히 반환하는 게 아니라 추출하는 것이므로 최댓값을 꺼내어 삭제함과 동시에 힙 구조가 유지되도록 재구성해야 한다.
추출은 우선 루트 노드의 값을 추출한 후, Heap의 마지막 요소를 루트 노드에 배치하고 루트 노드로부터 heapify를 수행하면 된다.
def extract_max(heap):
if len(heap) == 0:
print("heap is empty")
max_node = heap[1]
heap[1] = heap.pop()
max_heapify(heap, 1)
return max_node조금 전 만들었던 최대 힙에 대해 extract_max 함수를 써 보자.
heap = [None, 30, 15, 25, 5, 7, 13, 4]
print(extract_max(heap))
print(heap)>>> 30
>>> [None, 25, 15, 13, 5, 7, 4]Increase Value
Increase Value는 max heap에서 특정 노드의 값을 증가시키는 작업을 한다(min heap에서는 decrease value를 사용). 변경한 값이 heap 속성을 위배한다면 부모 노드가 더 큰 값이 될 때까지 부모 노드와 값을 바꾸는 작업을 진행한다.
def increase_value(heap, node:int, value:int):
if value < heap[node]:
print("New value must bigger than current value.")
return
heap[node] = value # 노드의 값을 새 값으로 변경
while (node > 1) and (heap[node] > heap[node//2]):
heap[node], heap[node//2] = heap[node//2], heap[node]
node = node // 2heap = [None, 20, 15, 17, 5, 7, 13, 4]
increase_value(heap, 4, 30)
heap>>> [None, 30, 20, 17, 15, 7, 13, 4]Insert
힙에 요소를 삽입할 때는 힙의 끝에 최솟값을 삽입한 뒤 increase_value 함수를 호출하여 해당 값을 삽입할 값으로 증가시킴과 동시에 힙 속성을 유지하도록 하면 된다.
def insert_value(heap, val: int):
heap.append(0)
increase_value(heap, len(heap)-1, val)heap = [None, 20, 15, 13, 5, 7]
insert_value(heap, 17)
heap>>> [None, 20, 15, 17, 5, 7, 13]Delete
힙에서 요소를 삭제할 때는 우선 increase_value를 이용해 삭제하고자 하는 노드의 값을 최댓값으로 바꾸고, extract_max를 이용해 해당 값을 추출하면 된다.
def delete_key(heap, node:int):
increase_value(heap, node, 999)
extract_max(heap)heap = [None, 20, 15, 17, 5, 7, 13]
delete_key(heap, 2)
heap>>> [None, 20, 13, 17, 5, 7]이렇게 빡시게 힙을 구현했지만, 사실 파이썬에서는 heapq라는 모듈을 사용해 손쉽게 힙을 구현할 수 있도록 해 두었다. 다만 힙을 직접 구현하는 과정에서 분명 배울 수 있는 것들이 있기도 하고, 단순히 라이브러리를 사용하기만 하는 것보다는 그 내부 원리를 이해하는 것이 중요하기도 하기 때문에 일일이 구현해 보았다.
