[Programmers/Python] 구현 - 최고의 집합

Programmers - 최고의 집합

---

문제

자연수 n 개로 이루어진 중복 집합(multi set, 편의상 이후에는 "집합"으로 통칭) 중에 다음 두 조건을 만족하는 집합을 최고의 집합이라고 합니다.

각 원소의 합이 S가 되는 수의 집합
위 조건을 만족하면서 각 원소의 곱 이 최대가 되는 집합
예를 들어서 자연수 2개로 이루어진 집합 중 합이 9가 되는 집합은 다음과 같이 4개가 있습니다.
{ 1, 8 }, { 2, 7 }, { 3, 6 }, { 4, 5 }
그중 각 원소의 곱이 최대인 { 4, 5 }가 최고의 집합입니다.

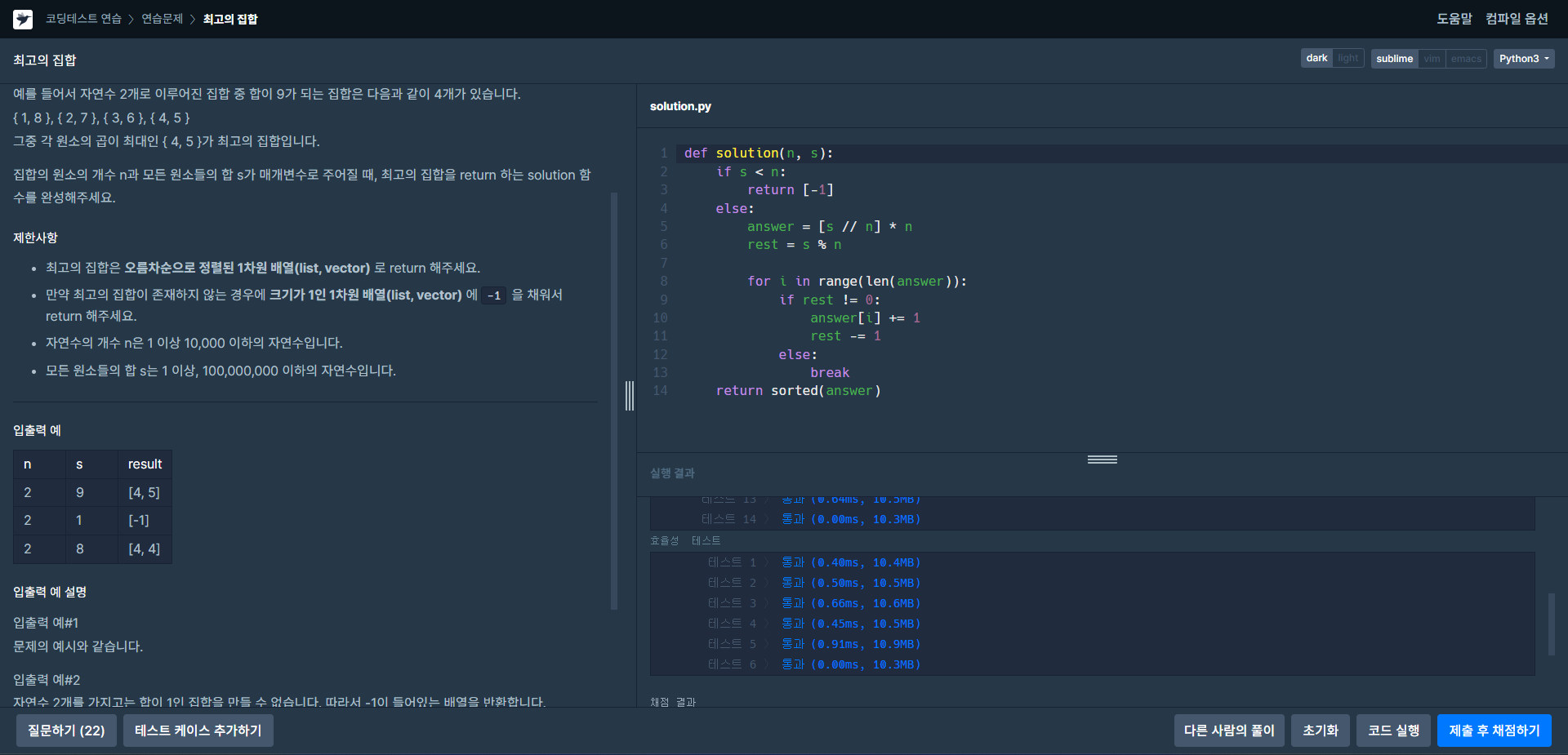
집합의 원소의 개수 n과 모든 원소들의 합 s가 매개변수로 주어질 때, 최고의 집합을 return 하는 solution 함수를 완성해주세요.

제한사항

• 최고의 집합은 오름차순으로 정렬된 1차원 배열(list, vector) 로 return 해주세요.
• 만약 최고의 집합이 존재하지 않는 경우에 크기가 1인 1차원 배열(list, vector) 에 -1 을 채워서 return 해주세요.
• 자연수의 개수 n은 1 이상 10,000 이하의 자연수입니다.
• 모든 원소들의 합 s는 1 이상, 100,000,000 이하의 자연수입니다.

입출력 예

n	s	result
2	9	[4, 5]
2	1	[-1]
2	8	[4, 4]

입출력 예 설명

• 입출력 예#1
  문제의 예시와 같습니다.
• 입출력 예#2
  자연수 2개를 가지고는 합이 1인 집합을 만들 수 없습니다. 따라서 -1이 들어있는 배열을 반환합니다.
• 입출력 예#3
  자연수 2개로 이루어진 집합 중 원소의 합이 8인 집합은 다음과 같습니다.
  { 1, 7 }, { 2, 6 }, { 3, 5 }, { 4, 4 }
  그중 각 원소의 곱이 최대인 { 4, 4 }가 최고의 집합입니다.

---

풀이

설계

1. 일단 n이 s보다 클 경우 자연수를 이용한 곱셈을 통해 s를 만드는 것이 불가능하므로 -1을 반환한다.

   n이 3일 경우 2를 만드는 것은 불가능하며, n이 5일 경우에도 4를 만드는 것은 불가능하다.

2. 두 수의 곱이 최대가 되려면 두 수의 차가 최소가 되어야 한다.

   예컨대 9를 만드는 수 중 {3, 6}의 차는 3으로 두 수의 곱은 18이 되지만, {4, 5}의 차는 1로 두 수의 곱은 20이 된다.
   3개의 수로 만드는 것을 가정했을 때에도, 13을 만들기 위한 수 중 {8, 3, 2}의 차를 합하면 5+1로 6이며 곱은 48이 된다.
   그러나 {4, 4, 5}의 경우 차의 합은 1이며 곱은 80이 된다.

3. 따라서 s를 n으로 나누어 각 몫을 리스트 answer로 만들고, 나머지가 존재할 경우 나머지를 1씩 나누어 answer의 요소에 순차적으로 더한다(나머지가 0이 되면 순회를 중단한다).
4. 오름차순 반환이므로 sorted(answer)를 반환한다.

코드

def solution(n, s):
    if s < n:
        return [-1]
    else:
        answer = [s // n] * n
        rest = s % n

        for i in range(len(answer)):
            if rest != 0:
                answer[i] += 1
                rest -= 1
            else:
                break
    return sorted(answer)