다이나믹 프로그래밍

다이나믹 프로그래밍이란?

하나의 문제를 단 한번만 풀도록 하는 알고리즘이다.
즉 이미 계산된 결과를 별도의 메모리 영역에 저장하여 다시 계산하지 않도록하게 한다.

1. 큰 문제를 작은 문제로 나누고, 작은 문제들의 답을 모아서 큰 문제를 해결
2. 동일한 작은 문제를 반복적으로 해결

위와 같은 두가지 조건을 만족 할 때, 사용한다.
일반적으로
1. 탑다운 == 하향식
2. 보텀업 == 상향식 방법이 있다.

대표적인 문제

피보나치수열

다이나믹 프로그래밍을 설명할 때, 피보나치수열로 예를 많이 든다.
하지만 그 전에, 피보나치 수열은 재귀함수를 공부할 때도 많이 나오는데,
재귀함수로 표현된 피보나치 수열을 먼저 보겠다.

def fibo(num) :
	if num <= 2 :
    	return 1
    return fibo(num-1) + fibo(num-2)

그런데 여기서 다이나밍 프로그래밍으로 구현하게 되면 다음과 같다.

# 하향식, 탑다운

arr = [0] * 100 # 100사이즈를 만든건 딱히 의미 없음. 
def fibo(num) :
	if num <= 2 :
    	return 1
 	if arr[num] != 0 :
    	return arr[num]
    arr[num] = fibo(num-1) + fibo(num-2)
    return arr[num]

# 상향식, 바텀업

arr =[0] * 100 # 필요한 범위를 미리 잡아준다..! 
arr[1] = 1
arr[2] = 1

num = int(input()) ## 99까지! 

for i in range(3, num+1) :
	arr[i] = d[i-1] + d[i-2]
   

그러면 재귀함수를 쓰지 않고, 다이나밍 프로그래밍을 사용해서 구현하는 이유는 뭘까?

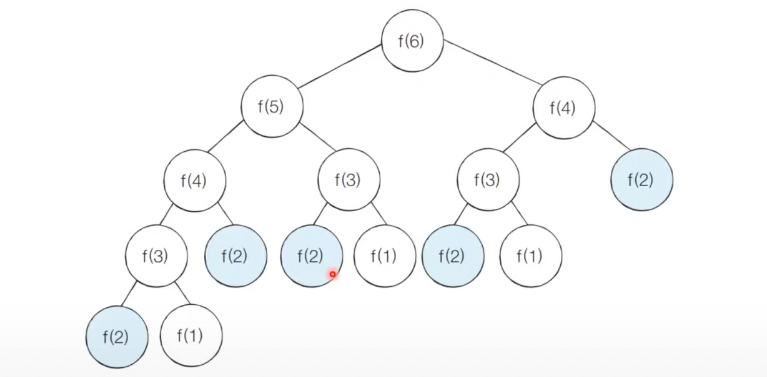
피보나치수열 6을 재귀로 호출 했을 때, 위와 같은 재귀함수가 호출되는 것을 볼 수 있다.
f(2)를 보면 f(2)를 여러번 호출 하는 것을 볼 수 있다. 즉 중복적으로 호출하는 것인데, 작은 수야 큰 무리가 없지만, fibo(30)만 계산하더라도 10억가량의 연산을 수행해야 된다.

그래서 한번 계산한 결과를 메모리에 저장하여 필요할 때 바로 꺼내서 사용 할 수 있기에 연산의 횟수를 줄일 수 있다.
즉 아래와 같이 색칠된 함수들만 처리가 됨을 알 수 있다.

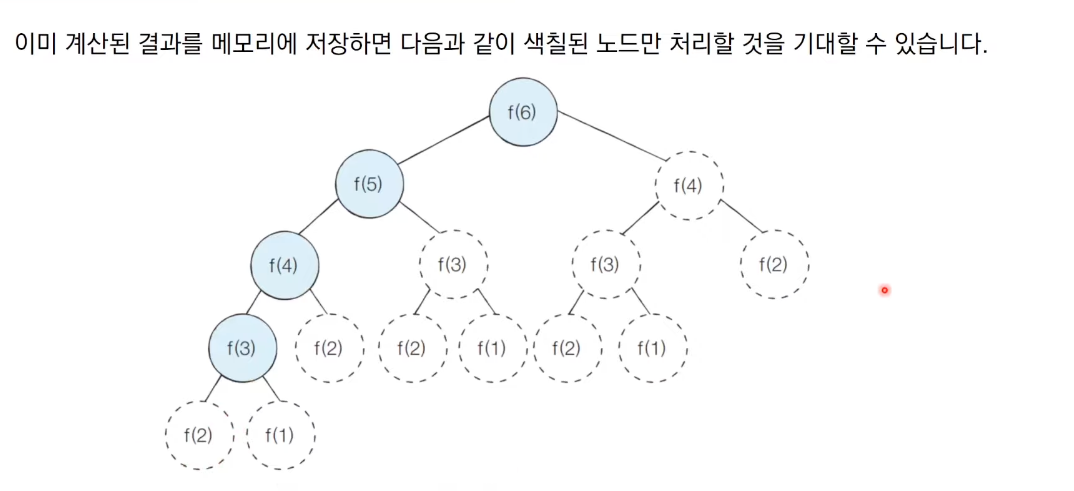
시간복잡도

이미 계산된 값들은 상수시간으로 필요할 때 찾아낼 수 있기 때문에,
시간복잡도는 O(N) 이 된다.