다이나믹프로그래밍 문제를 풀어나가면서 LCS를 마주했다
LCS는 https://youtu.be/EAXDUxVYquY 신찬수 교수님께서 잘 설명해주셔서 해당 강의를 듣고 개념을 정리했고, 개념을 정리한 바탕으로 문제를 풀었다.
내가 마주한 문제는 백준의 9251번 문제이고 링크는 아래와 같다. https://www.acmicpc.net/problem/9251
LCS 란?
두 문자열이 주어졌을 때, 가장 긴 공통 부문자열을 찾는 것이다.
여기서 부문자열은 문자열에서 몇개를 지우고 남은 문자열을 의미한다.
X = ['A','B','C','B','D','A','B']
Y = ['B','D','C','A','B','A']이렇게 두 문자열이 존재할때,
공통 부문자열은 ABA, BCBA 이다.
ABA 는
X 문자열에서 2,3,4,6 번째 인덱스를 지우면 ABA 가 남고,
Y 문자열에서 0,1,2 번째 인덱스를 지우면 ABA 가 남는다.
그래서 ABA 는 공통 부문자열이다.
BCBA는
X 문자열에서 0,4,6 번째 인덱스를 지우면 BCBA 가 남고,
Y 문자열에서 1,3 번째 인덱스를 지우면 BCBA 가 남는다.
그래서 BCBA 는 공통 부문자열이다.
그런데 우리가 찾고 싶은 LCS 는 가장 긴 공통 부문자열을 뜻하기 때문에
길이가 4인 BCBA 이다.
그런데 중요한건 이것을 어떻게 코드로 구현할 수 있는가? 이다.
LCS 구현
가장 긴 공통 부문자열을 찾기 위해서는 DP 즉 다이나믹 프로그래밍 접근을 활용하여 찾아낼 수 있다.
다이나믹 프로그래밍에 대한 정리는 아래 링크를 살펴보면 된다.
https://velog.io/@minpic/다이나믹-프로그래밍
우선 X 와 Y의 문자열이 있다고 가정을 하겠다.
X의 문자열이 "X1,X2,X3 ... Xi"
Y의 문자열이 "Y1,Y2,Y3 ... Yj"
가 존재한다고 해보자.
우리는 가장 긴 공통 부문자열을 찾는 것이기 때문에,
만약 Xi 와 Yj 가 같은 글자라면,
앞에 "X1 부터 Xi-1" 와 "Y1 부터 Yj-1" 까지 찾은 공통 부문자열의 길이에서 +1을 해줄 수 있을 것이다.
=> LCS(i-1,j-1) +1
그런데 만약 Xi 와 Yj 가 다른 글자라면,
공통 부문자열로 Xi와 Yj 가 동시에 뽑힐 수가 없다.
Xi가 뽑힐 수도 있고 안뽑힐 수도 있고, Yj가 뽑힐 수도 있고 안뽑힐 수 도 있지만, 둘이 다른 글자이기 때문에 동시에는 뽑힐 수가 없다.
=> max(LCS(i,j-1), LCS(i-1,j))
해당 점화식을 가지고 코드를 구현하려면 2차원 배열로 구성해 볼 수 있다.
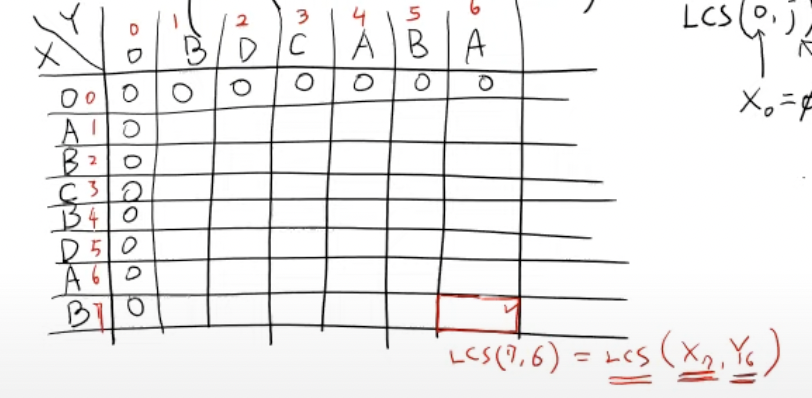
X와 Y의 글자가 같다면 행렬[i-1][j-1] 값에 +1 을 해주어서 [i][j] 자리에 넣어주면 되고,
X와 Y의 글자가 다르다면 행렬[i][j-1] 의 값과 행렬[i-1][j]값 중에 더 큰 값을 행렬[i][j]에 넣어주면 된다.

