Transitive closure (이행적 폐쇄)
Transitive closure matrix 는 한국어로 이행적 폐쇄 행렬 이다.
풀어서 설명하면 어떠한 그래프가 있을 때,
어떠한 정점 i 로 부터 j까지 갈 수 있다면 1을 표시하는 행렬이다.
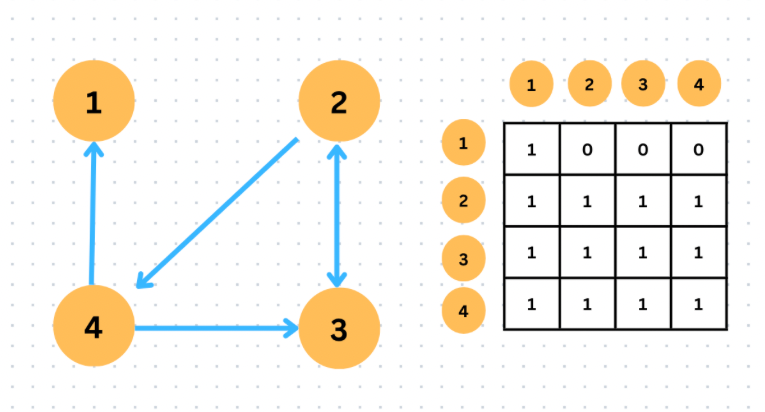
(i,j) 로 행렬을 표시해본다면,
(1,1) 은 자기 자신이기 때문에 갈 수 있어서 1
(1,2) 는 1에서 어떠한 정점으로 나갈 수 있는 간선이 없기 때문에 0.
(1,3)과 (1,4)도 (1,2)와 같은 이유로 0.
(2,1) 은 2->4->1 로 갈 수 있기에 1.
(2,2) 는 자기 자신이기 떄문에 갈 수 있어어 1.
(2,3) 은 갈 수 있기에 1.
(2,4) 는 갈 수 있기에 1.
(3,1) 은 3->2->4->1 로 갈 수 있기에 1.
...생략.
이러한 방법으로 이행적 폐쇄 행렬을 나타낼 수 있다.
그렇다면 해당 이행적 폐쇄 행렬을 어떻게 구할 수 있을까?
플로이드 워샬 알고리즘을 활용하여 해당 이행적 폐쇄 행렬을 나타낼 수 있다.
위에 나타낸 행렬처럼 바로 이행적 폐쇄 행렬을 나타내지 않고
i 에서 j 로 바로 갈 수 있는지 여부를 먼저 확인한다.
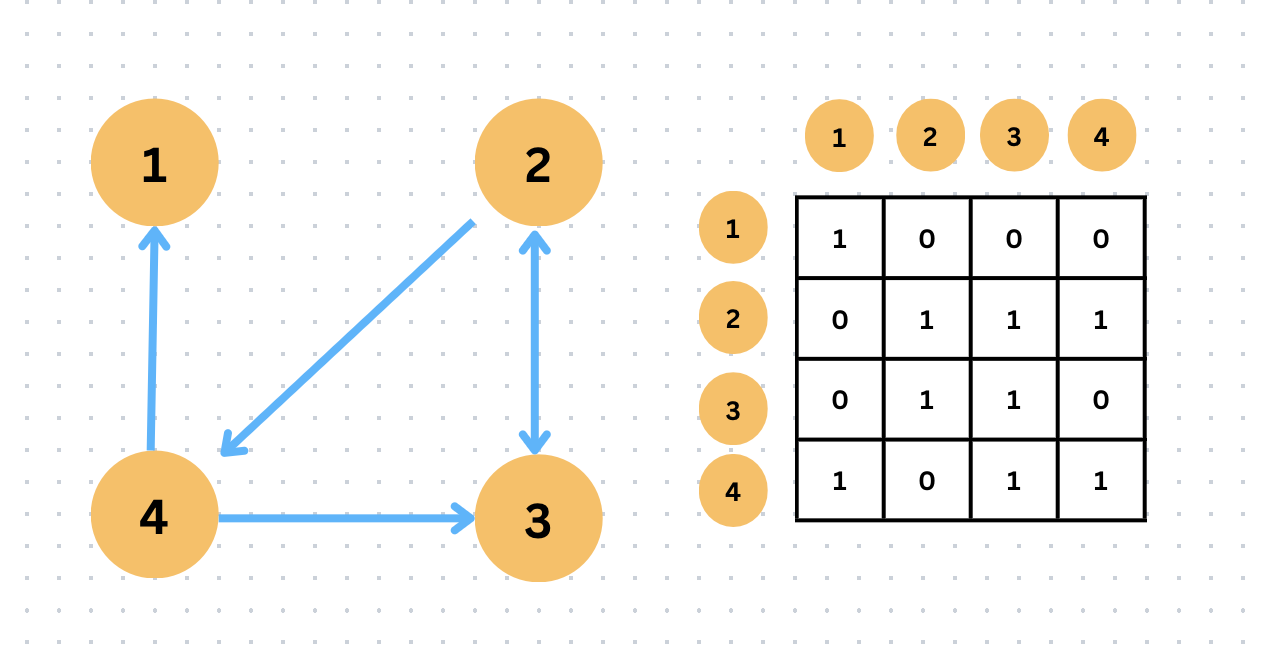
(1,1) 은 자기 자신이라서 1
(1,2) (1,3) (1,4) 는 갈 수 없어서 0
(2,1) 은 바로 가는 선이 없기 떄문에 0
(2,2) 자기 자신이라서 1
(2,3) 바로 가는 선이 있어서 1
(2,4) 바로 가는 선이 있어서 1
(3,1) 바로 가는 선이 없어서 0
(3,2) 바로가는 선이 있어서 1
(3,3) 자기 자신이라서 1
(3,4) 바로 가는 선이 없어서 0
(4,1) 바로가는 선이 있어서 1
(4,2) 바로가는 선이 없어서 0
(4,3) 바로가는 선이 있어서 1
(4,4) 자기 자신이라서 1
이렇게 구현하고 난 행렬을 T(0) 이라고 부른다.
그리고 나서 T(0)을 기본으로 T(1)을 만들것이다.
T(1)의 의미는 1 정점을 꼭 거쳐서 i -> 1 -> j 를 가겠다는 의미이다.
T(1) 의 테이블을 구성하려면,
T(0)을 기준으로 (i,j) 값과 ((i,1) AND (1,j))의 값 중에 큰 값을 입력하는 것이다.
코드로 나타내면 아래와 같다.
reach[i][j] = reach[i][j] or (reach[i][1] and reach[1][j]);
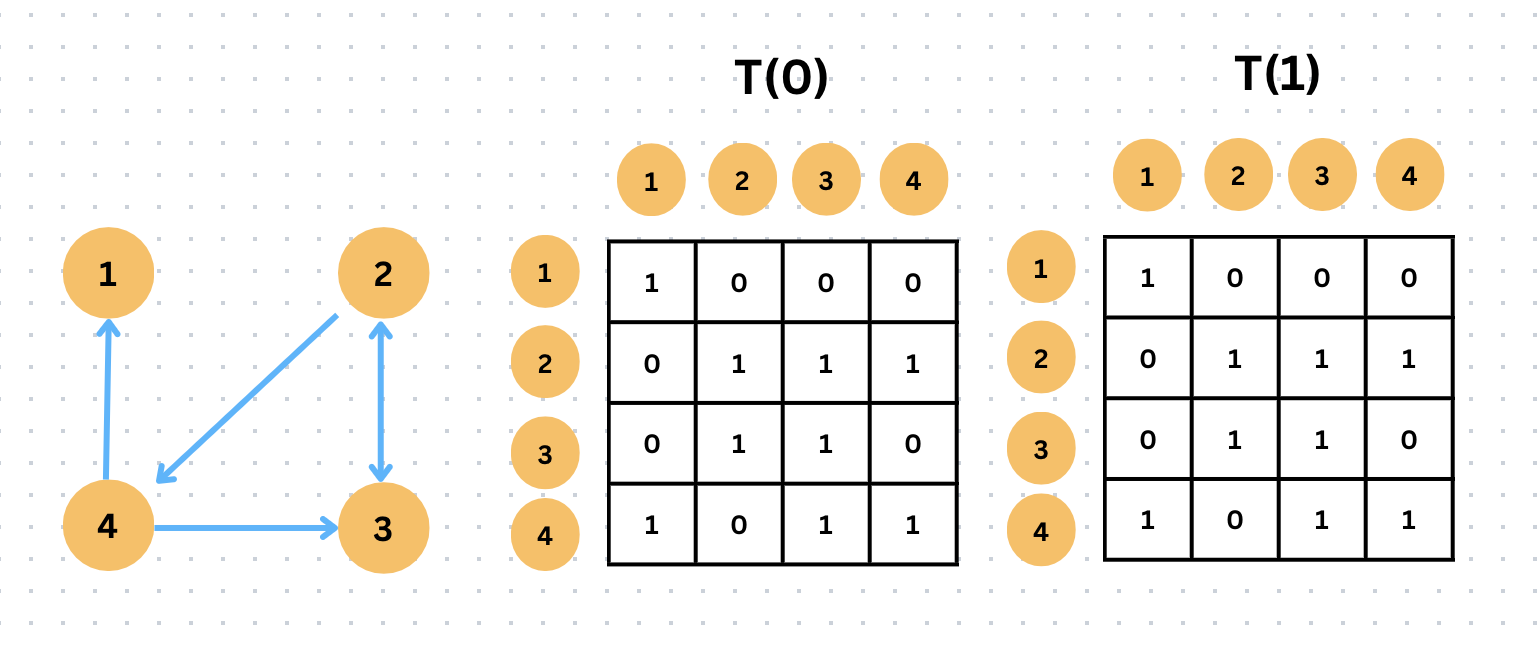
(1,1) = 1
(1,1) = 1 AND (1,1) = 1
1과 1의 OR 연산은 1 이다. 그래서 T(1) 에 (1,1)에 1을 넣는다.
(1,2) = 0
(1,1) = 1 AND (1,2) = 0
0 과 0 의 OR 연산은 0이다. (1,2) = 0 을 넣는다.
(1,3) = 0
(1,1) = 1 AND (1,3) = 0
0 과 0 의 OR 연산은 0이다. (1,3) = 0 을 넣는다.
(1,4) = 0
(1,1) = 1 AND (1,4) = 0
0 과 0 의 OR 연산은 0이다. (1,4) = 0 을 넣는다.
(2,1) = 0
(2,1) = 0 AND (1,1) = 1
0과 0 의 OR 연산은 0이다. (2,1) = 0 을 넣는다.
(2,2) = 1
(2,1) = 0 AND (1,2) = 0
1과 0 의 OR 연산은 1이다. (2,2) = 1 을 넣는다.
(2,3) = 1
(2,1) = 0 AND (1,3) = 0
1과 0 의 OR 연산은 1이다. (2,3) = 1 을 넣는다.
(2,4) = 1
(2,1) = 0 AND (1,4) = 0
1과 0 의 OR 연산은 1이다. (2,4) = 1 을 넣는다.
이러한 방식으로 (4,4) 까지 채워나가면 위에 이미지와 같은 T(1) 행렬이 나온다.
그런 다음 또 T(2)를 만드는데, 이번엔 T(0) 대신 T(1)을 기준으로 또 만들어준다.
그리고 이렇게 T(4)까지 만들어준다. 왜냐하면 정점이 4까지 있기 때문에 4까지만 만들면 된다.
결국 모든 정점을 거쳐서 (i,j) 까지 갈 수 있는지 확인하기 위해서이다.
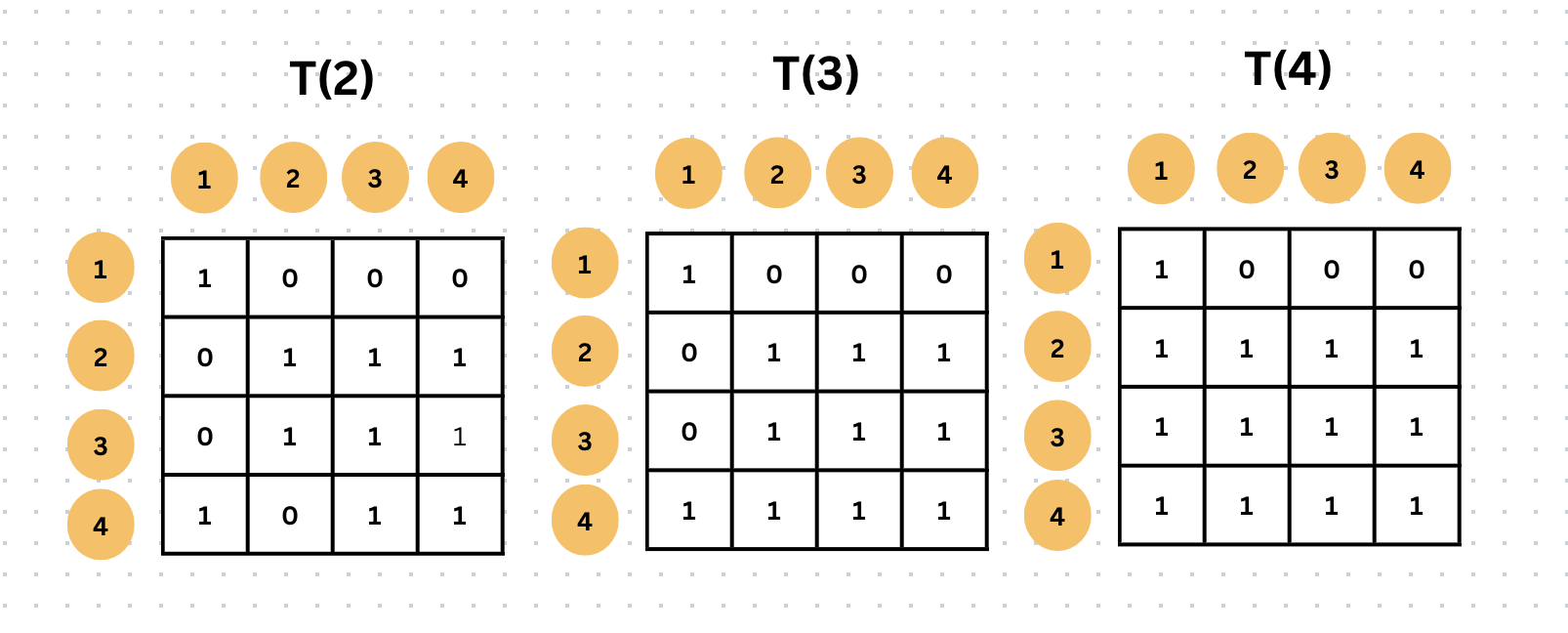
이렇게 T(4) 까지 구했다면 T(4)가 처음에 눈으로 확인했던 이행적 폐쇄 행렬이 된다.
해당 로직을 수도코드로 표현하면 다음과 같다.

for 문을 중첩으로 3번 사용하게 되면서,
시간복잡도는 O(n^3) 이다.
