단반향 연결리스트
단방향 연결리스트 기본 구조체
class Node {
String data;
Node next = null;
public Node() {
this.data = null;
this.next = null;
}
public Node (String d) {
this.data = d;
this.next = null;
}
}단방향 연결리스트에서 노드 추가
void insertNode(int d) {
Node newNode = new Node(d);
Node n = this;
while(n.next != null) {
n = n.next;
}
n.next = newNode;
}단방향 연결리스트에서 중간 노드 삭제
Node deleteNode(Node head, String d) {
Node n = head;
if(n.data == d) {
return head.next; // head를 움직인다.
}
while(n.next != null) {
if(n.next.data == d) {
n.next = n.next.next;
return head; // head는 그대로 있음
}
n = n.next;
}
return head;
}연결리스트에서 노드를 삭제하는 연산은 꽤 직관적이다.
노드 n이 주어지면, 그 이전 노드 prev를 찾아 prev.next를 n.next와 같도록 설정한다.
리스트가 양방향 연결리스트인 경우
n.next가 가리키는 노드를 갱신하여 n.next.prev가 n.prev와 같도록 설정해야 한다. 여기서 유의해야 할 점은 두 가지다.
- 널 포인터 검사를 반드시 해야한다.
- C나 C++처럼 메모리 관리가 필요한 언어를 사용해 구현하는 경우에는 삭제한 노드에 할당되었던 메모리가 제대로 반환되었는지 반드시 확인해야 한다.
단방향 연결리스트 출력
void printNode() {
Node n = this;
while(n != null) {
System.out.print(n.data);
n = n.next;
}
}면접 문제
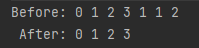
[2.1] 중복 없애기
정렬되어 있지 않은 연결리스트가 주어졌을 때 이 리스트에서 중복되는 원소를 제거하는 코드를 작성하라.
해법 1 (버퍼 O)
void deleteDups(Node head) {
HashSet set = new HashSet();
Node previous = null;
while(head != null) {
if(set.contains(head.data)) {
previous.next = head.next;
} else {
set.add(head.data);
previous = head;
}
head = head.next;
}
}연결리스트에서 중복되는 원소를 제거하기 위해서는 원소들을 추적할 수 있어야 한다. 여기서는 간단하게 해시테이블을 사용하여 처리하였다.단순히 연결리스트를 순횐하면서 각 원소를 해시테이블에 저장하였다. 그러다 중복된 원소를 발견하면, 그 원소를 제거한 뒤 계속 진행한다. 연결리스트를 사용하고 있으므로, 한 번의 순회로 전부 처리할 수 있다.
시간 복잡도: O(N) ,공간 복잡도: O(N)
해법 2 (버퍼 X)
void deleteDups2(Node head) {
Node current = head;
while(current != null) {
Node runner = current;
while(runner.next != null) {
if(runner.next.data == current.data) {
runner.next = runner.next.next;
}
else {
runner = runner.next;
}
}
current = current.next;
}
}버퍼가 없다면 두 개의 포인터를 사용해서 문제를 해결할 수 있다. current 포인터는 연결리스트를 순회하고, runner 포인터는 current포인터 뒤에 중복되는 원소가 있는지 확인하면 된다.
시간 복잡도: O(N^2), 공간 복잡도: O(1)
가만히 있는 current를 기준으로 current.next를 초기화를 하지 않고 매 순간 움직이는 runner를 기준으로 잡고 runner.next를 초기화 해야한다.
2.2 뒤에서 k번째 원소 구하기
단방향 연결리스트가 주어졌을 때 뒤에서 k번째 원소를 찾는 알고리즘을 구현하라.
해법 1. 연결리스트 길이를 아는 경우
Node solve1(Node head, int k) {
int cnt = 0;
while(head != null) {
if(cnt == size-k) {
return head;
}
cnt++;
head = head.next;
}
return head;
}만일 연결리스트의 길이를 알고 있다면, 맨 마지막 원소에서 k번째 오는 원소는 (N-k)번째 원소가 된다. 따라서 단순히 연결리스트를 순회해서 이 원소를 찾으면 된다.
시간 복잡도: O(N) ,공간 복잡도: O(1)
해법 2. 재귀적 방법
static int index = 0;
Node solve2(Node head, int k) {
index = 0;
if(head == null) { // 노드 끝까지 들어가서 리턴
return null;
}
Node node = solve(head.next, k); // 노드 끝까지 들어감
index++; // 리턴하면서 index를 하나씩 올려준다.
if(index==k) {
return head;
}
return node;
}코드 해설
1. 노드 맨 마지막까지 재귀함수로 들어간다.
2. 노드 맨 마지막에 도착하면 리턴하면서 정적 index를 한개씩 카운터 해준 후 index==k가 되는 순간의 노드를 리턴한다.
시간 복잡도: O(N), 공간 복잡도: O(N)
코드 결과
해법 3. 순환적(iterative) 방법
static int size=0;
Node nthTolast(Node head, int k) {
Node p1 = head;
Node p2 = head;
for(int i=0; i<k-1; i++) {
if(p2 == null) return null;
p2 = p2.next;
}
while(p2.next != null) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
}직관적이지는 않지만 좀 더 최적인 방법은, 순환적으로 푸는 것이다. 두 개의 포인터 p1과 p2를 사용한다. p1는 연결리스트의 시작 노드를 가리키고, p2는 k 노드만큼 움직여서 p1과 p2가 k 노드만큼 떨어져 있도록 만든다. 그런 다음, p1과 p2를 함께 이동시키면 p2는 N-k번 노드, 그러니까 뒤에서부터 k번째 노드를 가리키게 된다.