면접문제
4.1 노드 사이의 경로
방향 그래프가 주어졌을 때 두 노드 사이에 경로가 존재하는지 확인하는 알고리즘을 작성하라.
해결 방법
- 인접 행렬 또는 인접리스트를 이용한다.
소스 코드
import java.util.*;
class Main {
private static final int MAX = 4;
private static final int COUNT = 5;
static boolean[][] visited = new boolean[MAX][MAX];
static ArrayList<ArrayList> graph = new ArrayList<>();
public static void main(String[] args) {
for(int i=0; i<MAX; i++) {
graph.add(new ArrayList<>());
}
// 랜덤좌표(중복x)로 인접행렬, 인접리스트 만들기
random();
// 인접행렬로 경로존재 확인
matrix();
// 인접리스트로 경로존재 확인
for(int i=0; i<MAX; i++) {
adjList(i);
}
}
static void random() {
// 랜덤 중복값 예외
HashSet<Pair> position = new HashSet<Pair>();
while(position.size() < COUNT){
int u = (int) ((Math.random() * MAX));
int v = (int) ((Math.random() * MAX));
position.add(new Pair(u, v));
}
Iterator<Pair> it = position.iterator();
while(it.hasNext()) {
Pair pair = it.next();
int u = pair.u;
int v = pair.v;
// 2차원 배열로 표시
visited[u][v] = true;
// 인접리스트로 표시
graph.get(u).add(v);
}
/*
for(Pair pair : position) {
int u = pair.u;
int v = pair.v;
visited[u][v] = true;
graph.get(u).add(v);
}
*/
}
// 2차원 배열
static void matrix() {
for(int i=0; i<MAX; i++) {
for(int j=0; j<MAX; j++) {
if(visited[i][j]) System.out.println(i + "(은)는 " + j + "(와)과 연결되었습니다.");
}
}
System.out.println();
}
// 인접리스트
static void adjList(int start) {
for(int i=0; i<graph.get(start).size(); i++) {
int next = (int) graph.get(start).get(i);
System.out.println(start + "(은)는 " + next + "(와)과 연결되었습니다.");
}
}
private static class Pair {
int u, v;
Pair(int u, int v) {
this.u = u;
this.v = v;
}
}
}두 방법은 시간 복잡도의 차이가 있다.
인접 행렬
시간 복잡도: O(1)인접 리스트
시간 복잡도: 최악의 경우 O(N),
ex) {{1, 2}, {1, 3}, {1, 4}}가 연결되었을때 1과 4의 연결여부를 알려면
1: 2 3 4 순서대로 모두 탐색해야 하기 때문에 O(N)4.2 최소 트리
오름차순으로 정렬된 배열이 있다. 이 배열 안에 들어 있는 원소는 정수이며 중복된 값이 없다고 했을 때 높이가 최소가 되는 이진 탐색 트리를 만드는 알고리즘을 작성하라.
해결 방법
- 배열 가운데 원소를 트리에 삽입한다.
- 왼쪽 하위 트리에 왼쪽 절반 배열 원소들을 삽입한다.
- 오른쪽 하위 트리에 오른쪽 절반 배열 원소들을 삽입한다.
- 재귀 호출을 실행한다.
소스 코드
class Node {
int data;
Node left;
Node right;
Node(int d) {
this.data = d;
this.left = null;
this.right = null;
}
}
class Main {
final static int MAX = 7;
final static int[] sorted = new int[MAX];
public static void main(String[] args) {
for(int i=0; i<MAX; i++) sorted[i] = i;
Node root = createBst(sorted, 0, sorted.length-1);
printBst(root);
}
public static Node createBst(int[] sorted, int start, int end) {
if(start > end) return null;
int mid = (start + end) / 2;
Node n = new Node(sorted[mid]);
n.left = createBst(sorted, start, mid-1);
n.right = createBst(sorted, mid+1, end);
return n;
}
public static void printBst(Node root) {
if(root != null) {
String answer = "";
answer += "data: " + root.data;
if(root.left != null) {
answer += " left: " + root.left.data;
}
if(root.right != null){
answer += " right: " + root.right.data;
}
System.out.println(answer);
printBst(root.left);
printBst(root.right);
}
}
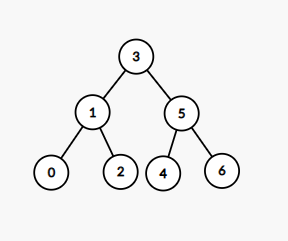
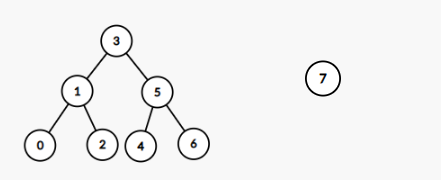
}트리 그림
출력
data: 3 left: 1 right: 5
data: 1 left: 0 right: 2
data: 0
data: 2
data: 5 left: 4 right: 6
data: 4
data: 6
전위 순회를 통해 보기 쉽게 출력했다.
Node n = new Node(sorted[mid]);
n.left = bst(sorted, start, mid-1);
n.right = bst(sorted, mid+1, end);
의 범위를 실수하는 일을 방지하자. 항상 가운데 원소를 넣기 때문에 가운데 원소는 빼줘야 한다.
4.3 깊이의 리스트
이진 트리가 주어졌을 때 같은 깊이에 있는 노드를 연결리스트로 연결해 주는 알고리즘을 설계하라. 즉, 트리의 깊이가 D라면 D개의 연결리스트를 만들어야 한다.
해결 방법
- 너비 우선 탐색을 이용한다.
- i번째 깊이에 도달했을 때 i-1번째 깊이에 해당하는 노드들은 전부 방문한 상태가 된다.
- 즉, i번째 깊이에 어떤 노드들이 있는지 알아내려면, i-1번째 깊이에 있는 노드의 모든 자식 노드를 검사하면 된다.
소스 코드
import java.util.ArrayList;
import java.util.LinkedList;
class Node {
int data;
Node left;
Node right;
Node(int d) {
this.data = d;
this.left = null;
this.right = null;
}
}
class Main {
final static int MAX = 7;
final static int[] sorted = new int[MAX];
public static void main(String[] args) {
for(int i=0; i<MAX; i++) sorted[i] = i;
Node root = createBst(sorted, 0, sorted.length-1);
ArrayList<LinkedList<Node>> result = new ArrayList<>();
result = bfs(root);
for(int i=0; i<result.size(); i++) {
System.out.println("depth: " + i);
int pos = 0;
for(Node n : result.get(i)) {
if(pos == 0) System.out.print(n.data);
else System.out.print(" → " + n.data);
pos++;
}
System.out.println("\n");
}
}
public static Node createBst(int[] sorted, int start, int end) {
if(start > end) return null;
int mid = (start + end) / 2;
Node n = new Node(sorted[mid]);
n.left = createBst(sorted, start, mid-1);
n.right = createBst(sorted, mid+1, end);
return n;
}
public static ArrayList<LinkedList<Node>> bfs(Node root) {
ArrayList<LinkedList<Node>> result = new ArrayList<>();
LinkedList<Node> current = new LinkedList<>();
if (root != null) {
current.add(root);
}
while(current.size() > 0) {
result.add(current);
LinkedList<Node> parents = current;
current = new LinkedList<>();
for(Node parent : parents) {
if (parent.left != null) {
current.add(parent.left);
}
if (parent.right != null) {
current.add(parent.right);
}
}
}
return result;
}
}4.2에서 만든 bst를 이용했다.
트리 그림
출력
depth: 0
node: 3depth: 1
node: 1 → 5depth: 2
node: 0 → 2 → 4 → 6
4.4 균형 확인
이진 트리가 균형 잡혀있는지 확인하는 함수를 작성하라. 이 문제에서 균형 잡힌 트리란 모든 노드에 대해서 왼쪽 부분 트리의 높이와 오른쪽 부분 트리의 높이의 차이가 최대인 트리를 의미한다.
해결 방법
- 트리의 루트부터 재귀적으로 하위 트리를 훑어 나가면서 그 높이를 검사한다.
- 각 노드에서 checkHeight를 사용해서 왼쪽 하위 트리와 오른쪽 하위 트리의 높이를 재귀적으로 구한다.
- 하위트리가 균형 잡힌 상태일 경우 checkHeight 메서드는 해당 하위 트리의 실제 높이를 반환한다.
- 그렇지 않은 경우에는 에러(Integer.MIN_VALUE)를 반환한다. 에러가 반환된 경우 즉시 실행을 중단한다.
소스 코드
import java.util.ArrayList;
import java.util.LinkedList;
class Node {
int data;
Node left;
Node right;
Node(int d) {
this.data = d;
this.left = null;
this.right = null;
}
}
class Main {
final static int MAX = 7;
final static int[] sorted = new int[MAX];
public static void main(String[] args) {
for(int i=0; i<MAX; i++) sorted[i] = i;
Node root = createBst(sorted, 0, sorted.length-1);
isBalnced(root);
// 노드 추가
root.left.left.left = new Node(7);
root.left.left.left.left = new Node(8);
System.out.println();
isBalnced(root);
}
public static Node createBst(int[] sorted, int start, int end) {
if(start > end) return null;
int mid = (start + end) / 2;
Node n = new Node(sorted[mid]);
n.left = createBst(sorted, start, mid-1);
n.right = createBst(sorted, mid+1, end);
return n;
}
static int checkHeight(Node root) {
if (root == null) return 0;
int leftHeight = checkHeight(root.left);
if(leftHeight == Integer.MIN_VALUE) return Integer.MIN_VALUE;
int rightHeight = checkHeight(root.right);
if(rightHeight == Integer.MIN_VALUE) return Integer.MIN_VALUE;
int heightDiff = leftHeight - rightHeight;
System.out.println("data: " + root.data + ", heightDiff: " + heightDiff);
if (Math.abs(heightDiff) > 1) {
return Integer.MIN_VALUE;
} else {
return Math.max(leftHeight, rightHeight) + 1;
}
}
static void isBalnced(Node root) {
if(checkHeight(root) != Integer.MIN_VALUE) System.out.println("균형 이진 트리 입니다.");
else System.out.println("불균형 이진 트리 입니다.");
}
}균형 이진 트리 예시
균형 이진트리는 4.2에서 만든 bst를 이용했다.
트리 그림
출력
data: 0, heightDiff: 0
data: 2, heightDiff: 0
data: 1, heightDiff: 0
data: 4, heightDiff: 0
data: 6, heightDiff: 0
data: 5, heightDiff: 0
data: 3, heightDiff: 0
균형 이진 트리 입니다.
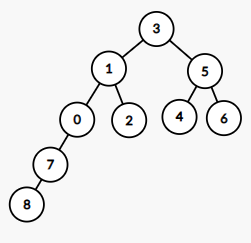
불균형 이진 트리 예시
불균형 이진트리는 4.2에서 만든 bst에 노드 2개룰 추가했다.
트리 그림
출력
data: 8, heightDiff: 0
data: 7, heightDiff: 1
data: 0, heightDiff: 2
불균형 이진 트리 입니다.
4.5 BST 검증
주어진 이진 트리가 이진 탐색 트리인지 확인하는 함수를 작성하라.
해결 방법 1. 중위 순회를 이용한다.
- 중위 순회를 하면서 배열에 원소들을 복사해 넣는다.
- 이 결과가 정렬된 상태인지 본다.
문제점
이 방법의 문제점은 트리 안에 중복된 값이 있는 경우를 처리할 수 없다.
예를 들어,
위 의 두 트리를 중위 순회하면 같은 결과가 나오기 떄문에 이들을 분간할 방법이 없다.
왼쪽트리는 유효한BST이지만오른쪽트리는 유효하지 않은 BST이다.하지만 트리에 중복된 값이 없다고 가정하면 올바르게 동작한다.
해결 방법 1. 소스 코드
import java.util.ArrayList;
import java.util.LinkedList;
class Node {
static int size = 0;
int data;
Node left;
Node right;
{
size++;
}
Node(int d) {
this.data = d;
this.left = null;
this.right = null;
}
}
class Main {
final static int MAX = 7;
final static int[] sorted = new int[MAX];
public static void main(String[] args) {
for(int i=0; i<MAX; i++) sorted[i] = i;
Node root = createBst(sorted, 0, sorted.length-1);
checkBST(root);
root.right.left.left = new Node(7);
checkBST(root);
deleteNode(root.right.left.left);
root.right.left.left = new Node(4);
checkBST(root);
}
public static Node createBst(int[] sorted, int start, int end) {
if(start > end) return null;
int mid = (start + end) / 2;
Node n = new Node(sorted[mid]);
n.left = createBst(sorted, start, mid-1);
n.right = createBst(sorted, mid+1, end);
return n;
}
static int index = 0;
static void copyBST(Node root, int[] array) {
if (root == null) return;
copyBST(root.left, array);
array[index++] = root.data;
copyBST(root.right, array);
}
static boolean checkBST(Node root) {
index = 0;
int[] array = new int[Node.size];
copyBST(root, array);
System.out.print("array[i]: ");
for(int i=1; i<Node.size; i++) {
if(array[i-1] >= array[i]) {
System.out.print(array[i-1] + " ");
System.out.println("\n이진 탐색 트리가 아닙니다.\n");
return false;
}
System.out.print(array[i-1] + " ");
}
System.out.print(array[Node.size-1]);
System.out.println("\n이진 탐색 트리입니다.\n");
return true;
}
static void deleteNode(Node root) {
root = null;
Node.size--;
}
}BST트리 O 예시
4.2에서 만든 bst를 이용했다.
트리 그림
출력
array[i]: 1 2 3 4 5 6
이진 탐색 트리입니다.
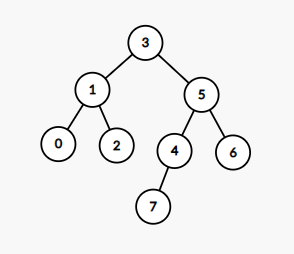
BST트리 X 예시
트리 그림
출력
array[i]: 1 2 3 7
이진 탐색 트리가 아닙니다.
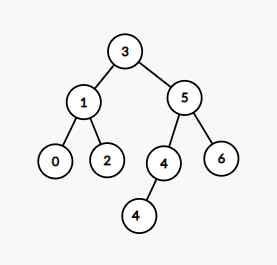
문제점이 발생하는 트리 예시
트리 그림
출력
array[i]: 1 2 3 4
이진 탐색 트리가 아닙니다.
위의 경우 BST트리가 맞지만 틀린 답이 나온다.
해결 방법 2. 최소 / 최대 기법
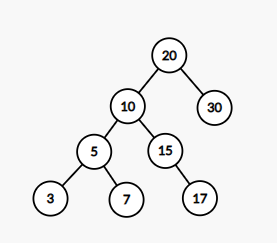
- 이진 탐색 트리의 정의를 이용하는 것이다. →
left.data <= current.data < right.data
이진 탐색 트리가 만족해야 하는 조건은 왼쪽의 모든 노드가 현재 노드보다 작거나 같고, 오른쪽의 모든 노드가 현재 노드보다 크다가 되어야 한다.
-
처음에는 (
min=null,max=null)에서 시작한다. 루트 노드가 이 조건을 만족함은 당연하다. (null은 min과 max가 존재하지 않는다는 뜻이다.) -
루트 노드의 왼쪽 노드들은 (
min=null,max=20)의 범위안에 있어야 하고, 오른쪽 노드들은 (min=20,max=null)의 범위 안에 있어야 한다. -
이 방법을 이용해 트리를 훑어 나간다. 왼쪽으로 분기하면 max를 갱신하고, 오른쪽으로 분기할 때는 min을 갱신한다. 언제든 범위에 어긋나는 데이터를 발견하면 트리 순회를 중단하고 false를 반환한다.
시간 복잡도: O(N)
공간 복잡도: O(logN)
해결 방법 2. 소스 코드
import java.util.ArrayList;
import java.util.LinkedList;
class Node {
static int size = 0;
int data;
Node left;
Node right;
{
size++;
}
Node(int d) {
this.data = d;
this.left = null;
this.right = null;
}
}
class Main {
final static int MAX = 7;
final static int[] sorted = new int[MAX];
public static void main(String[] args) {
for(int i=0; i<MAX; i++) sorted[i] = i;
Node root = createBst(sorted, 0, sorted.length-1);
isBST(root);
root.right.left.left = new Node(7);
isBST(root);
deleteNode(root.right.left.left);
root.right.left.left = new Node(4);
isBST(root);
}
public static Node createBst(int[] sorted, int start, int end) {
if(start > end) return null;
int mid = (start + end) / 2;
Node n = new Node(sorted[mid]);
n.left = createBst(sorted, start, mid-1);
n.right = createBst(sorted, mid+1, end);
return n;
}
static boolean checkBST(Node root) {
return checkBST(root, null, null);
}
static boolean checkBST(Node root, Integer min, Integer max) {
if (root == null) {
return true;
}
if((min != null && root.data <= min) || (max != null && root.data > max)) {
return false;
}
if(!checkBST(root.left, min, root.data) || !checkBST(root.right, root.data, max)) {
return false;
}
return true;
}
static void isBST(Node root) {
if(checkBST(root)) {
System.out.println("이진 탐색 트리입니다.");
} else {
System.out.println("이진 탐색 트리가 아닙니다.");
}
}
static void deleteNode(Node root) {
root = null;
Node.size--;
}
}순서대로 트리의 그림은 4.5 해결 방법 1의 예시들과 같다.
출력
이진 탐색 트리입니다.
이진 탐색 트리가 아닙니다.
이진 탐색 트리입니다.
4.6 후속자
이진 탐색 트리에서 주어진 노드의 '다음'노드(중위 후속자, in-order successor)를 찾는 알고리즘을 작성하라. 각 노드에는 부모 노드를 가리키는 링크가 존재한다고 가정하자.
해결 방법
-
가상의 노드 하나가 주어졌다고 해 보자. 중위 순회 순서는 왼쪽 하위트리, 현재 노드, 오른쪽 하위 트리다. 그렇다면 다음에 방문해야하 하는 노드는 오른쪽 어딘가에 있다. 그러면 이제 오른쪽 하위 트리가 있는 경우와 없는 경우로 나뉜다.
-
오른쪽 하위 트리가 있는 경우
오른쪽 하위 트리 중 어떤 노드일까? 오른쪽 하위 트리를 중위 순회 할 경우 처음으로 방문하게 되는 노드일 것이므로, 오른쪽 하위 트리에서 맨 왼쪽 아래에 놓일 것이다. -
오른쪽 하위 트리가 없는 경우
3-1. 어떤 노드 n의 오른쪽 하위 트리가 없다면, n의 하위 트리 방문은 끝난 것이다. 그렇다면 이제 n의 부모 노드 입장에서 어디까지 순회한 것인지를 알아내야 한다.n의 부모 노드를 q라고 하자.3-2.
n이 q의 왼쪽에 있었다면,다음에 방문할 노드는 q가 된다.(왼쪽→현재→오른쪽 순서이므로)3-3.
n이 q의 오른쪽에 있었다면,q의 오른쪽 하위 노드 탐색은 완전히 끝난것이다. 따라서q의 부모 노드 가운데 완전히 순회를 끝내지 못한 노드 x를 찾아야 한다.3.4 결국 n이 q의 왼쪽에 있는 상황을 찾아야 하는데, 왼쪽 노드를 발견하기전에 트리의 루트까지 올라가면 트리의 오른쪽 맨 끝 노드에 도달한 것이므로 다음 노드가 존재하지 않으므로, null을 반환해야 한다.
소스 코드
import java.util.ArrayList;
import java.util.LinkedList;
class Node {
static int size = 0;
int data;
Node left;
Node right;
Node parent;
{
size++;
}
Node(int d) {
this.data = d;
this.left = null;
this.right = null;
this.parent = null;
}
}
class Main {
final static int MAX = 7;
final static int[] sorted = new int[MAX];
public static void main(String[] args) {
for(int i=0; i<MAX; i++) sorted[i] = i;
Node root = createBst(sorted, 0, sorted.length-1);
setParent(root);
System.out.print("중위 순회 순서: ");
inOrderTraversal(root);
System.out.println();
// 루트: 3
printInOrderSucc(root);
// 맨오른쪽아래: 6
printInOrderSucc(root.right.right);
// 임의의 노드:4
printInOrderSucc(root.right.left);
}
public static Node createBst(int[] sorted, int start, int end) {
if(start > end) return null;
int mid = (start + end) / 2;
Node n = new Node(sorted[mid]);
n.left = createBst(sorted, start, mid-1);
n.right = createBst(sorted, mid+1, end);
return n;
}
public static void inOrderTraversal(Node n) {
if (n != null) {
inOrderTraversal(n.left);
System.out.print(n.data + " ");
inOrderTraversal(n.right);
}
}
static void setParent(Node n) {
if(n == null) {
return;
}
if(n.left != null) {
n.left.parent = n;
setParent(n.left);
}
if(n.right != null) {
n.right.parent = n;
setParent(n.right);
}
}
static Node inOrderSucc(Node n) {
if (n == null) {
return null;
}
/* 오른쪽 자식이 존재 > 오른쪽 하위 트리에서 맨 왼쪽 아래 노드를 반환한다.*/
if(n.right != null) {
return leftMostChild(n.right);
} else {
Node q = n;
Node x = n.parent;
// 노드가 오른쪽이 아닌 왼쪽에 있을 때까지 위로 올라간다.
while(x != null && x.left != q) {
q = x;
x = x.parent;
}
return x;
}
}
static Node leftMostChild(Node n) {
if (n == null) {
return null;
}
while(n.left != null) {
n = n.left;
}
return n;
}
static void printInOrderSucc(Node n) {
Node nextNode = inOrderSucc(n);
if(nextNode == null) {
System.out.println("현재 노드" + n.data + "(은)는 트리의 오른쪽 맨 끝 노드입니다.");
} else {
System.out.println("현재 노드" + n.data + "의 다음 중위 후속자는 " + nextNode.data + "입니다.");
}
}
}트리 그림
출력
중위 순회 순서: 0 1 2 3 4 5 6
현재 노드3의 다음 중위 후속자는 4입니다.
현재 노드6(은)는 트리의 오른쪽 맨 끝 노드입니다.
현재 노드4의 다음 중위 후속자는 5입니다.
이런 문제를 풀 떄는 실제로 순회가 이루어지는 절차를 주의 깊에 생각하고 의사코드를 먼저 작성해서 고려해야 할 경우들을 미리 그려보자.
4.7 순서 정하기
프로젝트의 리스트와 프로젝트들 간의 종속 관계(즉, 프로젝트 쌍이 리스트로 주어지면 각 프로젝트 쌍에서 두 번째 프로젝트가 첫 번째 프로젝트에 종속되어 있다는 뜻)가 주어졌을 때, 프로젝트를 수행해 나가는 순서를 찾으라. 유효한 순서가 존재하지 않으면 에러를 반환한다.
해결 방법
소스 코드
4.8 첫 번째 공통 조상
이진 트리에서 노드 두 개가 주어졌을 때 이 두노드의 첫 번째 공통 조상을 찾는 알고리즘을 설계하고 그 코드를 작성하라. 자료구조내에 추가로 노드를 저장해 두면 안 된다. 반드시 이진 탐색 트리일 필요는 없다.
해결 방법
-
이진 탐색 트리라면 두 노드에 대한 find 연산을 변경하여 어디서 경로가 분기하는지 찾을 수 있었을 것이다. 하지만 불행히도 이진 탐색 트리가 아니므로 다른 방법을 찾아봐야 한다. (물론 내 예제는 이진 탐색 트리지만 무시하자.)
-
노드 p와q의 공통 조상 노드를 찾기 위해서 가장 먼저 해야 할 일 중 하나는, 트리의 노드가 부모 노드에 대한 링크를 갖고 있는지 확인하는 것이다.
해결 방법 1. 부모 노드에 대한 링크가 있는 경우
- 부모로의 링크가 존재한다면 p와 q에서 시작해서 둘이 만날 때 까지 위로 올라가면 된다.
1. p와 q중 깊이가 높은 노드는 p와 q의 깊이 차이 절대값 만큼 올라가서 시작점을 똑같이 한다.
2. 그리고 둘이 만날 때 까지 쭉 위로 올라간다.
해결 방법 1. 소스 코드
class Node {
static int size = 0;
int data;
Node left;
Node right;
Node parent;
{
size++;
}
Node(int d) {
this.data = d;
this.left = null;
this.right = null;
this.parent = null;
}
}
class Main {
final static int MAX = 7;
final static int[] sorted = new int[MAX];
public static void main(String[] args) {
for(int i=0; i<MAX; i++) sorted[i] = i;
Node root = createBst(sorted, 0, sorted.length-1);
setParent(root);
// 3, 1
System.out.println(root.data + "번 노드와 " + root.left.data+ "번 노드의 공통 조상은 " + commonAncestor(root, root.left).data + "번 노드 입니다.");
// 0, 6
System.out.println(root.left.left.data + "번 노드와 " + root.right.right.data+ "번 노드의 공통 조상은 " + commonAncestor(root.left.left, root.right.right).data + "번 노드 입니다.");
// 0, 2
System.out.println(root.left.left.data + "번 노드와 " + root.left.right.data+ "번 노드의 공통 조상은 " + commonAncestor(root.left.left, root.left.right).data + "번 노드 입니다.");
}
public static Node createBst(int[] sorted, int start, int end) {
if(start > end) return null;
int mid = (start + end) / 2;
Node n = new Node(sorted[mid]);
n.left = createBst(sorted, start, mid-1);
n.right = createBst(sorted, mid+1, end);
return n;
}
public static void setParent(Node n) {
if(n == null) {
return;
}
if(n.left != null) {
n.left.parent = n;
setParent(n.left);
}
if(n.right != null) {
n.right.parent = n;
setParent(n.right);
}
}
public static Node commonAncestor(Node p, Node q) {
int delta = depth(p) - depth(q);
Node first = delta > 0 ? q : p; // 높이가 더 낮은 노드
Node second = delta > 0 ? p : q; // 높이가 더 깊은 노드
second = goUpBy(second, Math.abs(delta)); // 깊이가 깊은 노드를 위로 올려 시작점을 맞춘다.
// 두 노드가 언제 처음으로 교차하는지 찾는다.
while (first != second && first != null && second != null) {
first = first.parent;
second = second.parent;
}
return first == null || second == null ? null : first;
}
public static Node goUpBy(Node n, int delta) {
while (delta > 0 && n != null) {
n = n.parent;
delta--;
}
return n;
}
public static int depth(Node n) {
int depth = 0;
while (n != null) {
n = n.parent;
depth++;
}
return depth;
}
}트리 그림
출력
3번 노드와 1번 노드의 공통 조상은 3번 노드 입니다.
0번 노드와 6번 노드의 공통 조상은 3번 노드 입니다.
0번 노드와 2번 노드의 공통 조상은 1번 노드 입니다.
해결 방법 2. 부모 노드에 대한 링크가 없는 경우
해결 방법 2. 소스코드
4.9 BST 수열
배열의 원소를 왼쪽에서부터 차례로 트리에 삽입함으로써 이진 탐색 트리를 생성할 수 있다. 이진 탐색 트리 안에서 원소가 중복되지 않는다고 할 때, 해당 트리를 만들어 낼 수 있는 가능한 배열 모두 출력하라.
해결 방법
소스 코드
4.10 하위 트리 확인
두 개의 커다란 이진 트리 T1과 T2가 있다고 하자. T1이 T2보다 훨씬 크다고 했을 때, T2가 T1의 하위트리(subtree)인지 판별하는 알고리짐을 만들자. T1 안에 있는 노드 n의 하위 트리가 T2와 동일하면, T2는 T1의 하위 트리다. 다시 말해, T1에서 노드 n의 아래쪽을 끊어 냈을 때 그 결과가 T2와 동일 해야한다.
해결 방법 1. 각 트리의 순회 결과를 문자열로 나타내 비교
- 각 트리의 순회 결과를 문자열로 나타낸 뒤 이 둘을 비교해 볼 수 있다. 만일 T2가 T1의 하위 트리라면, T2의 순회 결과가 T1의 부분 문자열이 된다.
그렇다면 무슨 순회를 해야 할까?
중위 순회는 절대 아닐 것이다. 이진 탐색 트리를 중위 순회하면 항상 값이 정렬된 순서로 출력된다. 즉 값은 같지만 구조가 다른 두 이진 탐색 트리를 중위 순회하면 언제나 같은 결과가 나온다.
→ 무슨 말인지 모르겠으면 4.5 BST검증 문제를 보자.전위 순회를 할 경우에는 항상 첫번째 원소가 루트라는 사실을 알 수 있다. 그다음에는 왼쪽과 오른쪽 원소들이 차례대로 나온다. 하지만 전위 순회에서도 트리의 구조가 다를 경우 같은 결과가 나오기도 한다.
이를 해결 하는 방법은 'X'와 같이 널(null)노드를 나타내는 특변할 문자를 문자열에 나타내는 것이다.
따라서 왼쪽 트리를 전위 순회 할 경우 {20, 20, X}가 될것이고 오른쪽 트리를 순회 하면{20, X, 20}이 될 것이다.
소스 코드
class Node {
static int size = 0;
int data;
Node left;
Node right;
Node parent;
{
size++;
}
Node(int d) {
this.data = d;
this.left = null;
this.right = null;
this.parent = null;
}
}
class Main {
final static int MAX = 7;
final static int[] sorted = new int[MAX];
public static void main(String[] args) {
for(int i=0; i<MAX; i++) sorted[i] = i;
Node root = createBst(sorted, 0, sorted.length-1);
isSubtree(root, root.left);
isSubtree(root.left, root.right);
// 새로운 트리 생성
Node newRoot = new Node(7);
isSubtree(root, newRoot);
}
public static Node createBst(int[] sorted, int start, int end) {
if(start > end) return null;
int mid = (start + end) / 2;
Node n = new Node(sorted[mid]);
n.left = createBst(sorted, start, mid-1);
n.right = createBst(sorted, mid+1, end);
return n;
}
public static void isSubtree(Node t1, Node t2) {
if(containsTree(t1, t2)) {
System.out.println("T2(root:" + t2.data + ")는 T1(root:" + t1.data +")의 하위 트리 입니다.");
} else {
System.out.println("T2(root:" + t2.data + ")는 T1(root:" + t1.data +")의 하위 트리가 아닙니다.");
}
}
public static boolean containsTree(Node t1, Node t2) {
StringBuilder string1 = new StringBuilder();
StringBuilder string2 = new StringBuilder();
getOrderString(t1, string1);
getOrderString(t2, string2);
return string1.indexOf(string2.toString()) != -1;
}
private static void getOrderString(Node n, StringBuilder sb) {
if (n == null) {
sb.append('X'); // 널노드 문자 추가
return;
}
sb.append(n.data);
getOrderString(n.left, sb);
getOrderString(n.right, sb);
}
}트리 그림
출력
T2(root:1)는 T1(root:3)의 하위 트리 입니다.
T2(root:5)는 T1(root:1)의 하위 트리가 아닙니다.
T2(root:7)는 T1(root:3)의 하위 트리가 아닙니다.
해결 방법 2. 큰 트리에서 작은 트리를 찾는다.
이에 대한 대안은 더 큰 트리 T1을 탐색하는 것이다. T2의 루트와 같은 노드를 T1에서 발견할 때마다, mathTree를 호출한다. matchTree는 두 하위 트리가 동일한지 검사할 것이다.
실행 시간 분석은 다소 까다로울 수 있다. n이 T1의 노드 개수이고, m이 T2의 노드 개수일 때, 순진하게 실행 시간을 O(nm)이라고 답할 수 도 있다. 기술적으로는 맞는 말이지만, 한번 더 생각해 보면 조금더 정확한 상한을 찾아낼 수 있다.
T1의 모든 노드에서 matchTree를 호출하지 않는다. 대신, T2의 루트 노드값이 T1에 등장하는 빈도 k만큼만 호출한다. 따라서 실행 시간은 O(n+km)에 가깝다.
하지만 이것조차도 이 알고리즘의 실행 시간을 과대평가 한거다. 루트와 동일한 노드를 발견했다 하더라도, T1과 T2 간의 차이를 발견하는 순간 matchTree를 종료해버리기 때문이다. 따라서 matchTree에서 언제나 m개의 노드를 모두 살펴보는게 아니다.
해결 방법 2. 소스 코드
class Node {
static int size = 0;
int data;
Node left;
Node right;
Node parent;
{
size++;
}
Node(int d) {
this.data = d;
this.left = null;
this.right = null;
this.parent = null;
}
}
class Main {
final static int MAX = 7;
final static int[] sorted = new int[MAX];
public static void main(String[] args) {
for(int i=0; i<MAX; i++) sorted[i] = i;
Node root = createBst(sorted, 0, sorted.length-1);
isSubtree(root, root.left);
isSubtree(root.left, root.right);
// 새로운 트리 생성
Node newRoot = new Node(7);
isSubtree(root, newRoot);
}
public static Node createBst(int[] sorted, int start, int end) {
if(start > end) return null;
int mid = (start + end) / 2;
Node n = new Node(sorted[mid]);
n.left = createBst(sorted, start, mid-1);
n.right = createBst(sorted, mid+1, end);
return n;
}
public static void isSubtree(Node t1, Node t2) {
if(containsTree(t1, t2)) {
System.out.println("T2(root:" + t2.data + ")는 T1(root:" + t1.data +")의 하위 트리 입니다.");
} else {
System.out.println("T2(root:" + t2.data + ")는 T1(root:" + t1.data +")의 하위 트리가 아닙니다.");
}
}
public static boolean containsTree(Node t1, Node t2) {
if (t2 == null) return true;
return subTree(t1, t2);
}
private static boolean subTree(Node t1, Node t2) {
if (t1 == null) {
return false; // 큰 트리가 비어있으면 하위 트리를 찾지 못한다.
} else if (t1.data == t2.data && matchTree(t1, t2)) { // 데이터가 같으면 그 루트를 기준으로 match하기 시작함
return true;
}
return subTree(t1.left, t2) || subTree(t1.right, t2); //큰 T1트리에서 T2를 찾음
}
public static boolean matchTree(Node t1, Node t2) {
if (t1 == null && t2 == null) {
return true; // 하위 트리가 없다.
} else if (t1 == null || t2 == null) {
return false; // 하나의 트리만 비었을 때, 둘이 같지 않음
} else if (t1.data != t2.data) {
return false; // 값이 다를 때
} else {
return matchTree(t1.left, t2.left) && matchTree(t1.right, t2.right);
}
}
}트리 그림
출력
T2(root:1)는 T1(root:3)의 하위 트리 입니다.
T2(root:5)는 T1(root:1)의 하위 트리가 아닙니다.
T2(root:7)는 T1(root:3)의 하위 트리가 아닙니다.
간단한 형태의 첫 번째 방법(해결 방법 1)이 더 좋을 때는 언제고, 두 번째 방법(해결 방법 2)이 더 나은 경우는 언제일까?
-
먼저 살펴본 해결 방법1의 첫번째 방법은 O(n+m)의 메모리가 필요핟. 반면 두 번째 방법은 O(logn+logm)의 메모리가 필요하다.
규모 확장성 측면에서는 메모리 사용량 문제가 굉장히 중요하다는 사실을 기억하자. -
첫 번째 방법의 수행 시간은
O(n+m)이지만 두 번째 살펴본 방법은최악의 경우 O(nm)의 시간이 걸린다. 하지만 최악의 수행 시간은 시간 상한을 다소 느슨하게 표현하므로 좀 더 정확한 상한을 깊이 있게 살펴보자. -
좀 더 가까운 시간 상한은 위에서 말했다싶이
O(n+km)이다. 여기서k는 T2의 루트가 T1에 출현하는 빈도다. T1과 T2의 노드에 저장되는 값이 0과 p사이에서 생성된 난수값이라고 하자. 이때 k는 n/p에 가까울 것이다. 왜냐하면 T1의 노드 n개가 각각 T2의 루트와 같을 확률이 1/p이기 때문이다. 그러므로T1의 노드 가운데 n/p 노드가 T2.root와 같을 것이다.
따라서p=1000, n=1,000,000이고 m=100일 떄, 대략1,100,000개의 노드를 검사해야 한다.
n + m*n/p→ (1,100,000=1,000,000 + 100* 1,000,000/ 1000)
따라서 두 번째 살펴본 방법이 공간 효율성 측면에서 보다 최적의 해법이라는 사실은 분명하고, 시간적 측면에서도 보다 최적이다. 우리가 어떤 가정을 하느냐와 최악의 시간은 좀 느리더라도 평균적 수행시간을 줄이도록 할 것이냐의 여부에 달려있다.