[CS] Lecture6

Minsol·2024년 10월 15일
CS
0

🖥️CS

목록 보기
5/12

Chapter3: Arithmetic for Computer(컴퓨터의 산술 연산)

Zero, Infinity, NaN의 차이 (예외변수들)

Zero (0)

  • 지수(E)가 0이고 분수(F)가 0일때 0을 나타냄
  • 부호 비트(S)에 따라 +0 또는 -0을 나타낼 수 있음

Infinity (∞)

  • 최대의 E와 F=0으로 표현됨
    • Single precision(단정밀도, 8비트 지수): 최대 E = 255
      - Double precision(배정밀도, 11비트 지수): 최대 E = 2047
  • 오버플로우 혹은 0으로 나누기(n/0)와 같은 경우에 발생할 수 있음
  • 부호비트에 따라 ±∞

NaN(Not a Number)

  • 최대의 E와 F ≠ 0으로 표현됨
  • 0/0 또는 음수에 대한 제곱근(sqrt)과 같은 경우에 발생할 수 있음
  • NaN이 포함된 연산은 항상 NaN 결과를 반환함: Op(X, NaN) = NaN

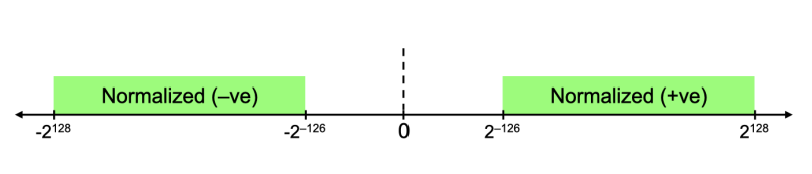
Denormal Numbers (비정규화 수)

  • 정규화 수는 특정 범위 내에서만 표현할 수 있기 때문에, 그보다 작은 값을 표현하려면 비정규화 수가 필요함 (비정규화 수: 정규화 수보다 작은 값을 나타냄, 거의 0에 가까움)
  • IEEE 표준에서 비정규화 수(denormalized numbers)를 사용하여 처리하는 방법
    • ±0과 가장 작은 정규화된 부동소수점 수 사이의 차이를 채움
    • 0으로의 점진적 언더플로우를 제공함 (즉, 값이 매우 작아지면 갑작스럽게 0이 되는 것이 아니라 점진적으로 0에 가까워짐) => 정밀도가 감소함


비정규화 수: 지수(E)가 모두 0일때 (Exponent = 000...0 Þ hidden bit is 0)

분수(F) 부분이 000...0인 비정규화 수는 0을 나타냄

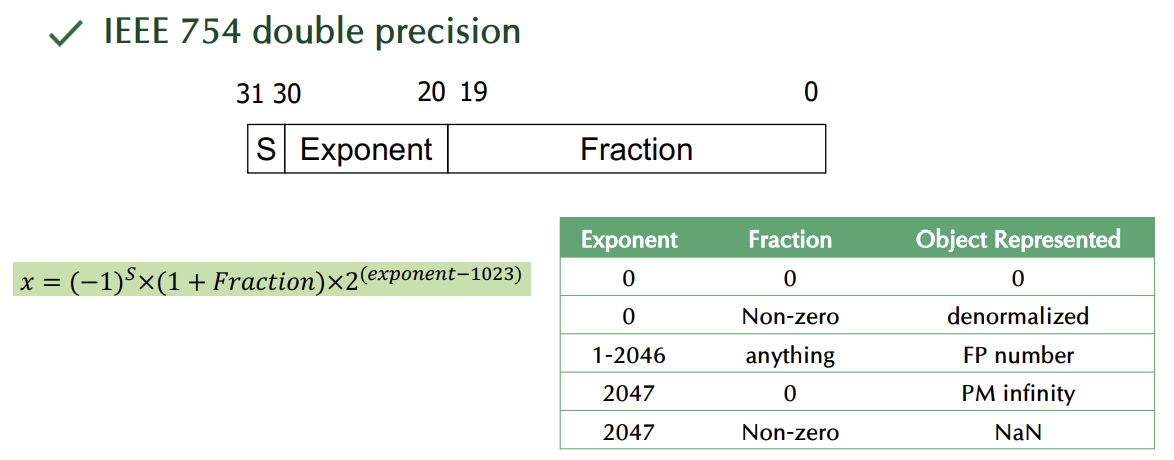
부동소수점 표현(Representation of Floating Point Numbers)


IEEE 754 단정밀도(single precision)

IEEE 754 배정밀도(double precision)

  • single일때와 똑같으나, 숫자만 차이

Floating Point의 덧셈, 곱셈 순서

Floating-Point Addition(덧셈)

4자리 10진수 덧셈

<덧셈 (양수 + 양수)> : 4자리 10진수(4-digit decimal)
1. 소수점(decimal points) 맞추기
지수가 작은 숫자를 지수가 큰 숫자에 맞춰서 이동
2. 가수(significands) 더하기
3. 정규화 및 오버플로우, 언더플로우 확인하기
정규화된 결과는 가수가 1 이상 10 미만이 되도록 함 -> 기본 골자: x.---
4. 반올림 및 필요시 재정규화
정밀도에 따라 반올림을 수행하고 다시 정규화함 -> 4개의 bit로 조정: x.xxx × 10ⁿ

4자리 2진수 덧셈

<덧셈 (양수 + 음수)> : 4자리 2진수(4-digit binary)
1. 이진 소수점(binary points) 맞추기
지수가 작은 숫자를 지수가 큰 숫자에 맞춰서 이동
2. 가수(significands) 더하기
3. 정규화 및 오버플로우, 언더플로우 확인하기
정규화된 결과는 가수가 1 이상 10 미만이 되도록 함 -> 기본 골자: x.---
4. 반올림 및 필요시 재정규화
정밀도에 따라 반올림을 수행하고 다시 정규화함 -> 4개의 bit로 조정: x.xxx × 2ⁿ

Floating-Point Multiplication(곱셈)

4자리 10진수 곱셈

  1. 지수(E) 더하기 -> 새 지수!
  2. 가수(significands) 곱하기
  3. 정규화 및 오버플로우, 언더플로우 확인하기 -> 기본 골자: x.---
  4. 반올림 및 필요시 재정규화 -> 4개의 bit로 조정: x.xxx × 2ⁿ
  5. 결과의 부호 결정함 -> 플러스 × 마이너스 = 마이너스

4자리 2진수 곱셈

  1. 지수(E) 더하기 -> 새 지수!
  2. 가수(significands) 곱하기
    • ex. Unbiased: -1 + -2 = -3
    • ex. Biased: (-1+127) + (-2+127) = -3 +254 -127 = -3 +127
      biased는 지수를 부호 없는 양수로 변환하여 처리하기 위함
      bias-> 단정밀도는 바이어스 값으로 127, 배정밀도는 1023을 사용
  3. 정규화 및 오버플로우, 언더플로우 확인하기 -> 기본 골자: x.---
  4. 반올림 및 필요시 재정규화 -> 4개의 bit로 조정: x.xxx × 2ⁿ
  5. 결과의 부호 결정함 -> 플러스 × 마이너스 = 마이너스

+) bias 적용의 실제 계산

  • 계산된 바이어스 지수 값은 저장 시에는 양수로 처리됨: (-1+127) + (-2+127)
  • 계산할때는 다시 바이어스값을 빼서 실제 지수 값을 복원함: -3 +254 -127 = 124

부동소수점 연산에서의 추가 비트들: Guard, Round, Sticky

내부 표현(Internal Representation)

부동 소수점 연산에서 사용하는 추가 3비트: Guard, Round, Sticky
이 비트들은 연산을 더 정확하게 하고, 하드웨어 복잡성을 줄이면서도 정확한 산술 연산을 가능하게 함

  • Guard Bit

    • 중요한 비트 손실을 방지하는 역할
    • 결과의 정확도를 유지하기 위해 하나의 guard bit 필요!
      • 정규화 과정에서 필요시 왼쪽으로 shift하며 이것을 마지막 fraction bit로 사용함

  • Round Bit, Sticky Bit

    • 반올림을 위한 비트들
      • Round bit: Guard 비트 뒤
      • Sticky bit: Round 비트 뒤로, 모든 추가 비트들의 OR 연산 결과를 나타냄 (round의 정확도를 위해)

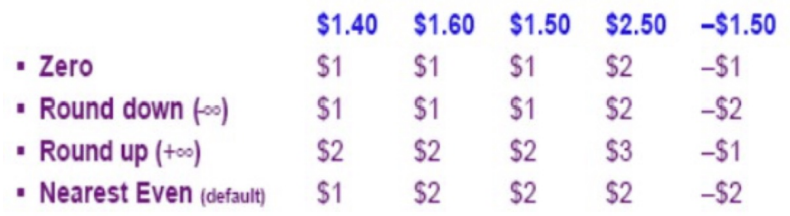
IEEE 754 표준의 네 가지 반올림 모드

  1. default mode: Round to Nearest Even (가장 가까운 짝수로 반올림)
  • g가 1이고, r 또는 s가 1인 경우 or g=1이고 r과 s가 0이며 f의 마지막이 1인 경우
  • 그 외에는 결과 가수를 1.f₁f₂…fl로 잘라냄
  1. Round toward +∞ (양의 무한대 방향으로 반올림)
  • 결과의 부호가 양수이고 g 또는 r 또는 s가 1인 경우, 결과를 증가시킴
  1. Round toward −∞ (음의 무한대 방향으로 반올림)
  • 결과의 부호가 음수이고 g 또는 r 또는 s가 1인 경우, 결과를 증가시킴
  1. Round toward 0 (0 방향으로 반올림)
  • 항상 결과를 잘라냄 (즉, 소수 부분을 그냥 제거함)

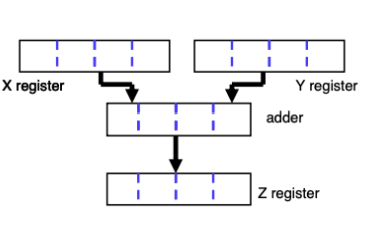
(SWP) SubWord Parallelism (서브워드 병렬성)

  • 서브워드 병렬성: 그래픽 및 오디오 어플리케이션에서 짧은 벡터에서 동시에 여러 연산을 수행하도록 하는 것
    • ex. 128bit adder에서 서브워드 병렬 연산 수행할 때
      • 16개의 8bit 덧셈
        • 8개의 16bit 덧셈
        • 4개의 32bit 덧셈
  • 이 방식은 데이터 수준의 병렬성, 벡터 병렬성, 단일 명령어 다중데이터(SIMD: Single Instruction Muptiple Data)라고도 불림
  • 목표: 효율성 향상 (== 워드 크기 자원 낭비를 피하는 것)
  • Subword: 워드 내에 포함된 작은 데이터 항목
  • 여러 서브워드를 하나의 워드에 압축하여 전체의 워드를 한번에 처리함 (서브워드에 대해 동시에 병렬처리)

Chapter4: The Prcessor

CPU (중앙처리장치)

  • 컴퓨터 시스템에서 명령어를 실행하고 계산을 수행하는 핵심 장치
  • CPU의 목적: 명령어 처리, 실행, 작업 수행, 프로그래밍 수행 등을 효율적으로 하게 함
  • 컴퓨터의 필수 구성 요소, 시슴템의 전체 성능을 결정함
    단일 사이클 CPU는 각 명령어가 단일 클록 사이클 내에 실행되는 CPU 아키텍처입니다.

Single-cycle CPU

  • 단순하고 직관적인 설계=> 각 명령어가 여러 단계로 나뉘어 한 cycle에서 순차 시행됨
  • 간단한 저전력 애플리케이션에서 사용됨
  • 주요 구성 요소
    • ALU(==arthmetic logic unit)(==산술 논리 장치), Control unit(제어 장치), memory(메모리), register(레지스터)
    • 명령어는 메모리에서 인출되고 해독된 후 실행됨 (fetch-decode-execute 사이클)
    • 명렁어 실행의 각 단계: 명령어 인출, 레지스터 읽기, ALU 연산, 메모리 접근 등의 작업
  • 장점
    • 단순하고 직관적 설계
    • 짧은 파이프라인 -> 복잡성 감소
    • 저전력 소비 (구성요소 적고 제어 회로 간단하여)
  • 단점
    • 효율성과 성능이 낮음
    • clock cycle 낭비: 모든 명령어가 같은 시간동안 실행되기 때문
    • 명령어 병렬 처리 x: 한 사이클에 하나의 명령어만 실행할 수 있음
    • 확장성 제한: 복잡한 애플리케이션에는 적합x

Multi-cycle CPU

  • 각 명령어가 여러 클록 사이클에 걸쳐 실행되는 CPU => 각 명령어가 여러 단계로 나뉘어 (순차 시행x!!) 동시에 실행될 수 있음

  • 효율성과 성능이 중요한 고성능 애플리케이션에서 사용됨

  • 주요 구성 요소

    • ALU(==arthmetic logic unit)(==산술 논리 장치), Control unit(제어 장치), memory(메모리), register(레지스터)
    • 여러 단계의 명령어 실행 프로세스를 따르고 각 단계에서 다른 작업이 동시에 수행
    • 명렁어 실행의 각 단계가 독립적으로 작동! -> 동시에 작동하기 위함

  • 장점

    • 더 높은 효율성과 성능(병렬시행이라서!)
    • 명령어 수준의 병렬성 활용(여러 명령어가 서로 다른 단계에서 동시 실행됨)
    • 복잡하고 고성능 애플리케이션에 적합

  • 단점

    • 더 복잡한 설계와 구현
    • 긴 파이프라인 및 높은 전력 소모 가능성
    • 제어 장치와 명령어 스케줄링의 복잡성 증가

    단일사이클 CPU와 멀티사이클 CPU의 성능 평가

  1. 명령어 실행 시간 비교
  • 단일 사이클 CPU: 고정된 실행시간으로 모든 명령어 실행됨
  • 멀티 사이클 CPU: 다양한 실행시간으로, 각 명령어가 여러 클록 사이클에 걸쳐 실행되기 때문에 명령어에 따라 실행 시간이 달라짐
  • 멀티 사이클 CPU의 실행시간이 더 빠름!(동시 처리이므로)
  1. 전체 효율성과 처리량에 미치는 영향
  • 단일 사이클 CPU: 고정된 실행 시간 -> 낮은 효율성, 처리량(고정된 클록 주기보다 빨리 실행될 수 있는 명령어가 다른 명령어 실행될때까지 대기해야하므로)
  • 멀티 사이클 CPU: 병렬적으로 명령어 실행 -> 높은 효율성, 처리량

단일사이클 CPU의 적용

  • PIC 마이크로컨트롤러(저전력장치), 초기 RISC 기반 프로세서
  • 임베디드 시스템, 소비자 전자 제품, IoT(사물 인터넷) 장치와 같은 애플리케이션

멀티사이클 CPU의 적용

  • Intel x86 프로세서, ARM 프로세서
  • 고성능 컴퓨팅, 서버, 데스크톱/노트북 컴퓨터에
  • 과학 시뮬레이션, 비디오 렌더링, 데이터 분석
profile
Minsol
👀
이전 포스트

[CS] Lecture5

다음 포스트

[CS] Lecture7

0개의 댓글