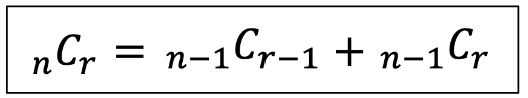Searching(탐색)

Linear Search(선형 탐색)

가장 간단한 알고리즘

• [0]: 목표 값이 포함되어 있으면 0을 반환, 없으면 다음으로 이동
• [1]: 목표 값이 포함되어 있으면 1을 반환, 없으면 다음으로 이동
  ...
• [N-1]:목표 값이 포함되어 있으면 N-1을 반환, 없으면 다음으로 -1을 반환
  => 시간복잡도: O(N)

Dictionary Search에 대한 비유(analogy)

• 영어 사전에서 단어를 검색한다고 가정할때, '선형 탐색' 방법을 사용하면 단어를 찾기 전에 몇 개의 단어를 볼 수 있나? -평균적으로, N/2 (N: 사전의 단어 수)
  

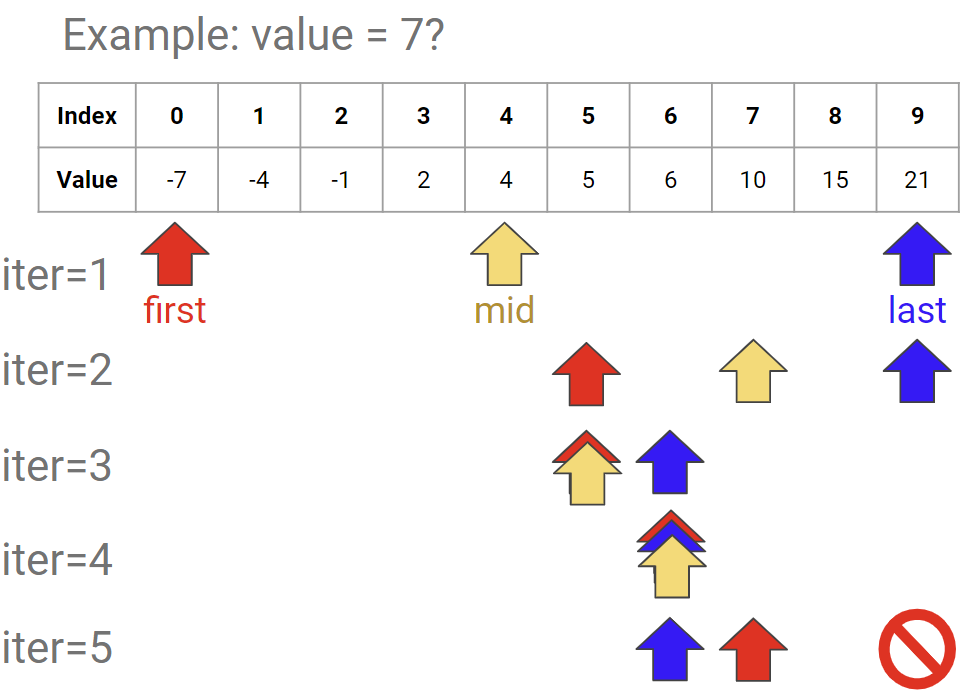
Binary Search(이진 탐색)

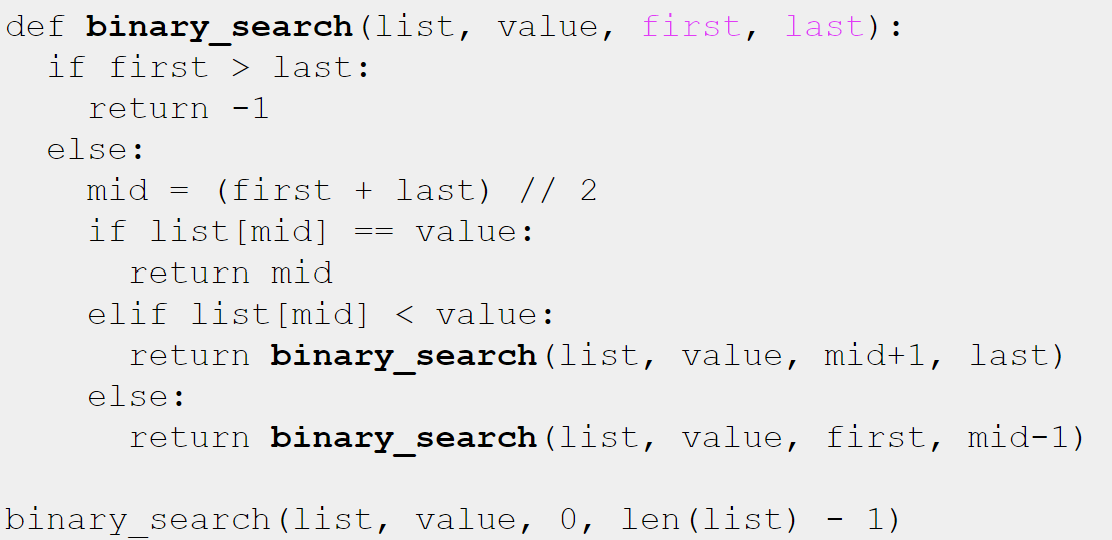
+)여기서 first, last, mid는 모두 index를 의미함
따라서, last = len(list)-1을 하는 이유!!

• Linear Search: sorted list에 적용될 수 있지만 sorted list의 이점을 활용하지 않음!
• Main Idea: 중간에 어떤 값이 저장되어 있는지 확인하기!
  • target보다 중간 값이 작으면 이전의 모든 값 ignore
  • target보다 중간 값이 크면 이후의 모든 값 ignore
    => 이후, 절반으로 줄어든 list에서 같은 과정을 반복함!!(반씩 줄이는 과정)
  • 존재하지 않는 값을 탐색중이라면?
    • list 반씩 줄이는 과정에서, list에 아무 값이 남지 않게 되면 (== 존재하지 않는 값을 탐색중인 것!)

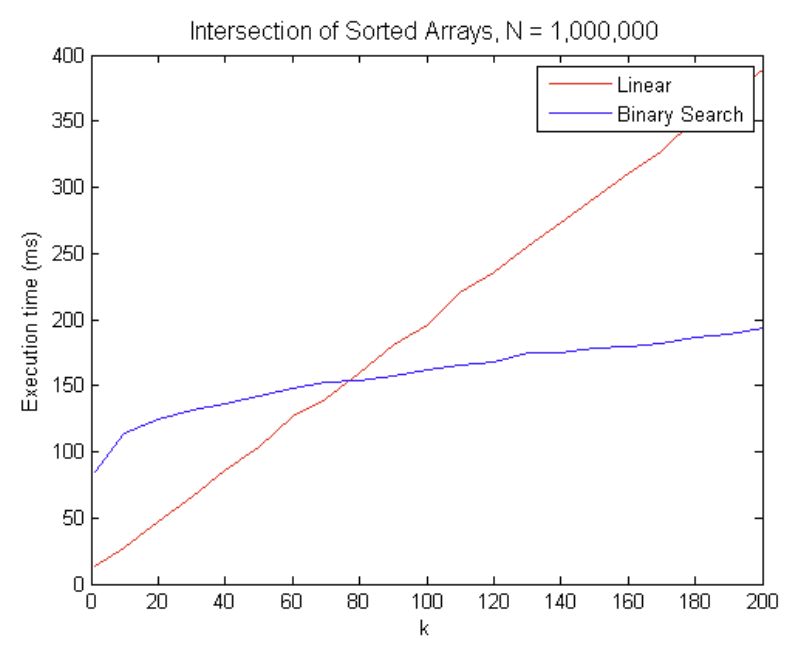
선형탐색과 이진탐색 시간복잡도 비교

• 선형 탐색

  • 모든 list에 적용 가능
  • 시간복잡도: O(N)

• 이진 탐색

  • sorted list에만 적용 가능
  • 시간복잡도: O(logN)

여전히 존재하는 문제점은...?

• 1) 이진 탐색이 중복(duplicate)이 존재하는 경우 작동 X!
  • 이러한 중복(duplicate)을 반환하려면?
  • 가장 왼쪽에 있는 것(leftmost one)을 반환하려면?
  • 가장 오른쪽에 있는 것(rightmost one)을 반환하려면?
• 2) query보다 크거나 같은 첫 번째 요소를 찾음

Recursion(재귀)

Recursion Algorithm(재귀 알고리즘)

• 하위 문제(subproblem)을 스스로 부르는 알고리즘
  • 하위 문제: 원래 문제와 정확히 같은 유형 but 규모(scale)이 더 작음
• "복잡한 문제를 더 간단하게 보기!!!"
• ex. 이진 탐색, 정렬(선택 정렬, 병합 정렬 등), 트리 횡단(tree traversal)

재귀 알고리즘의 기본 요소

• Base case: 알고리즘이 추가적인 재귀 호출(recursive call) 없이 쉽게 결론(trivally conclude)을 내릴 수 있는 가장 간단한 사례

  • ex. Searching의 empty list, Sorting의 single element
    =>이러한 경우는 O(1)로 간단하게 해결됨

• General case: 알고리즘은 동일한 문제를 더 작은 규모로 해결하기 위해 하나 이상의 재귀적 호출을 할 수 있어야함

  • Recursive call(재귀적 호출): 엄격하게 더 작아야 무한히 가지 않고 알고리즘이 끝이 날 수 있음..
  • 동일한 항목이 반복적으로 호출되지 않는지 확인하는 것이 매우 중요

• 명심할 것!!!!

  • 알고리즘은 가능한 모든 input에 대해 정답으로 마무리되어야하고, 이 알고리즘을 최대한 효율적으로 처리해야함

이진 탐색의 Recursive version

• 시간복잡도: O(logN)
  => 각 호출(call)은 mid의 계산/value 비교/output 반환에서 각각 O(1)이 소요됨

Problem1: Reversing a String

• 문자열 reverse 하기
  • ex. ACTGCC → CCGTCA

Problem2: Combination

• 비효율적임..

• Combination(조합): 선택 순서가 중요하지 않고, 전체 n개 중 r개 선택하는 것

• Recursive definition

  • C(n, r) = 1 if r = 0 or n
  • C(n, r) = 0 if r > n
  • C(n, r) = C(n - 1, r - 1) + C(n - 1, r)

재귀 요약

• 문제를 더 간단하게 해석할 수 있는 방법이 필요함
• 중복 계산이 있으면 매우 비효율적
• 알고리즘이 항상 종료할 기본 케이스를 충족해야함