[DS] Stacks & Queues

Minsol·2024년 10월 10일

📖DS

목록 보기

7/14

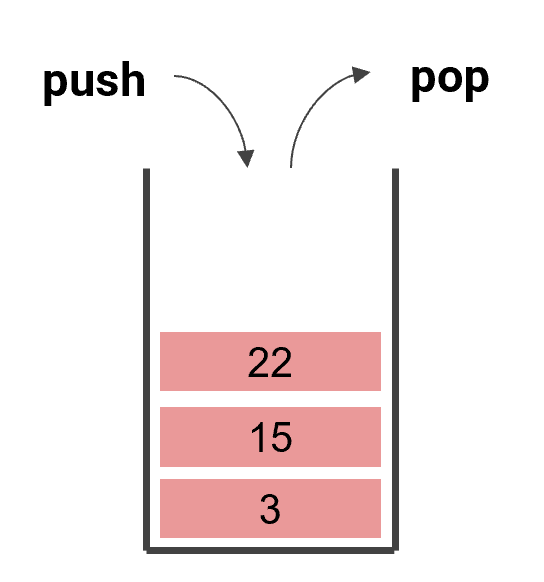
Stack(스택)

Last In, First Out (LIFO) => 마지막에 들어간 것이 먼저 나옴
가장 최근에 추가된 항목에만 접근 가능 (최근에만 접근)

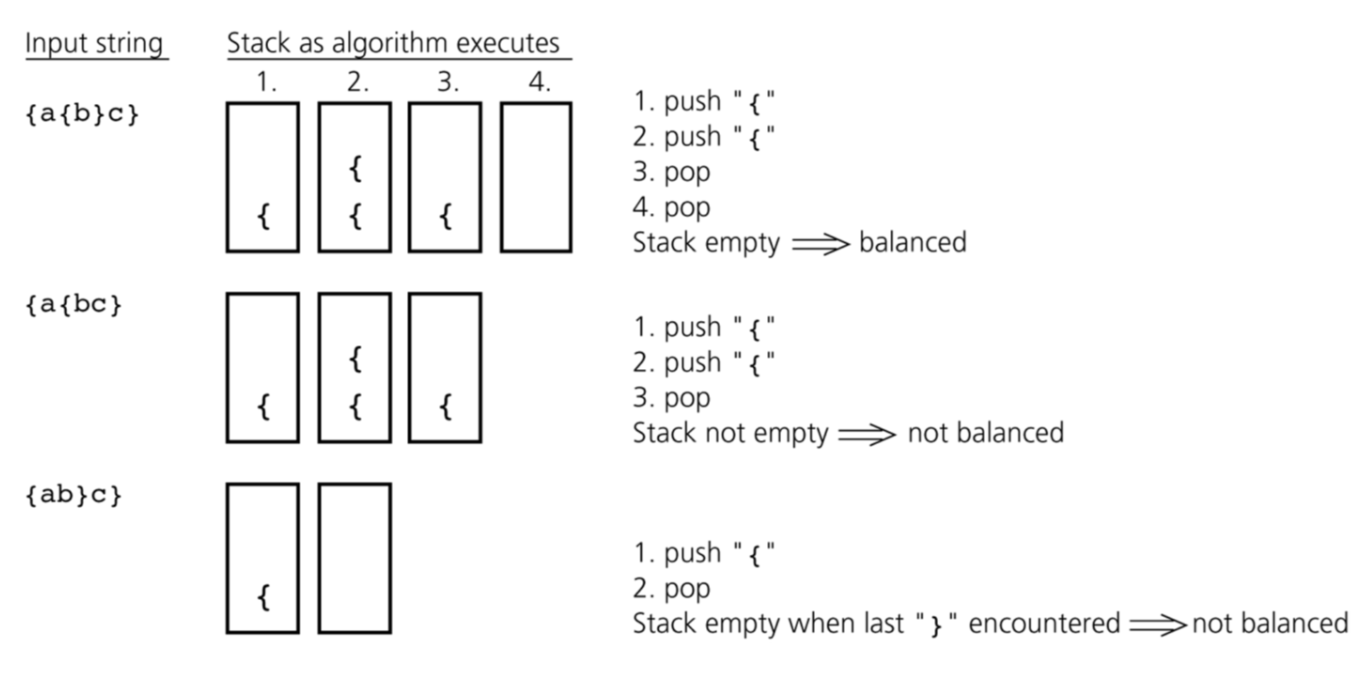
<예제1> Checking Balances of Braces (괄호의 균형 확인)

스택에 추가(push)되는 경우 -> {
스택에 삭제(pop)되는 경우 -> }

balanced 경우: stack이 마지막에 비어있을 때

not balanced 경우: stack이 마지막에 괄호가 남아있을 때 or
스택이 비어있는 상황에서 } 만났을 때

Stack Terminologies(용어)

새 항목 추가 => push
가장 최근 항목 가져오기(retrieving) => peek
항목 삭제 => pop

Stack Class Design

Array(배열)을 기반으로 stack을 구현함 => python list

stack에 항목을 저장하기 위한 내부 데이터 구조
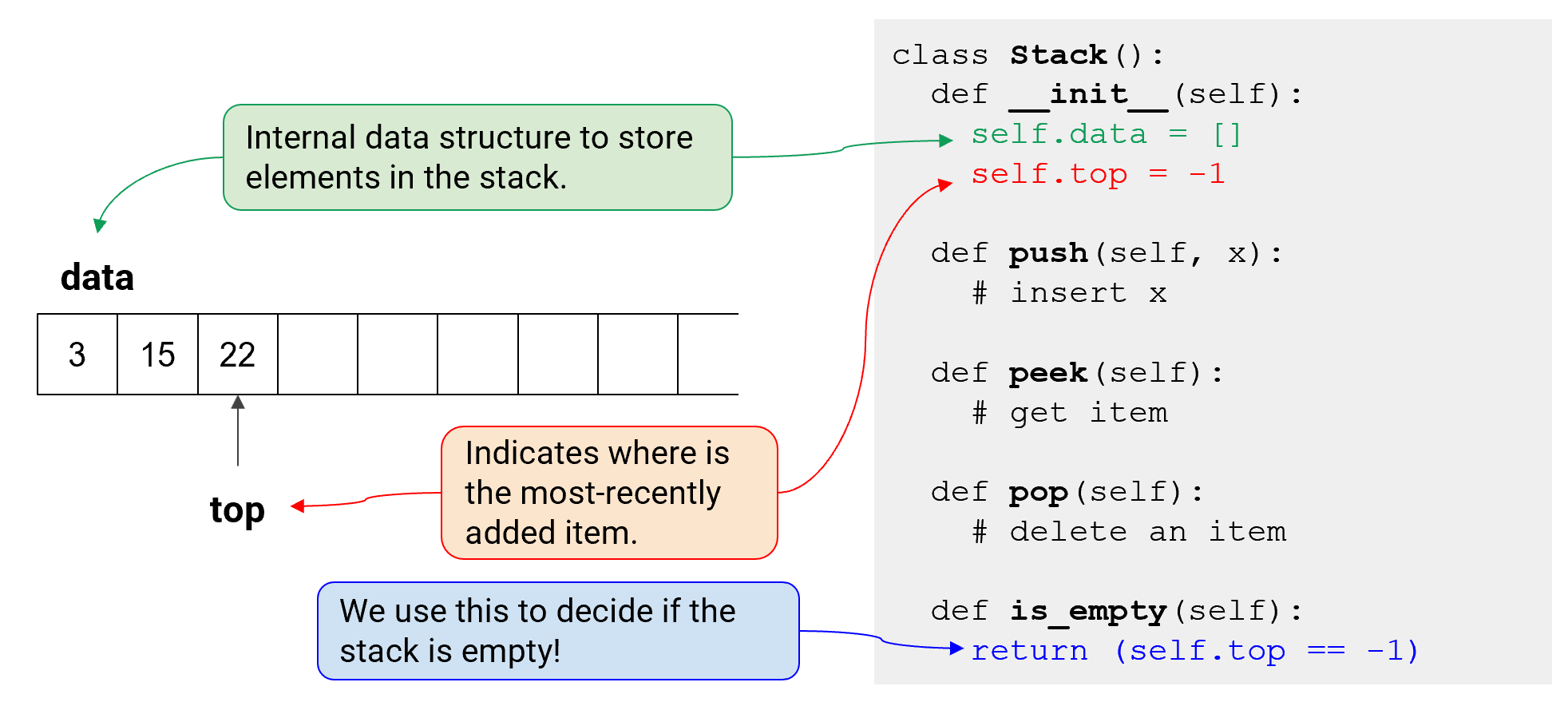
top: 가장 최근에 추가된 항목의 위치를 나타냄
return (self.top == -1) top의 index가 -1로 지정됨으로써 스택이 비어있는지 판단하게 됨

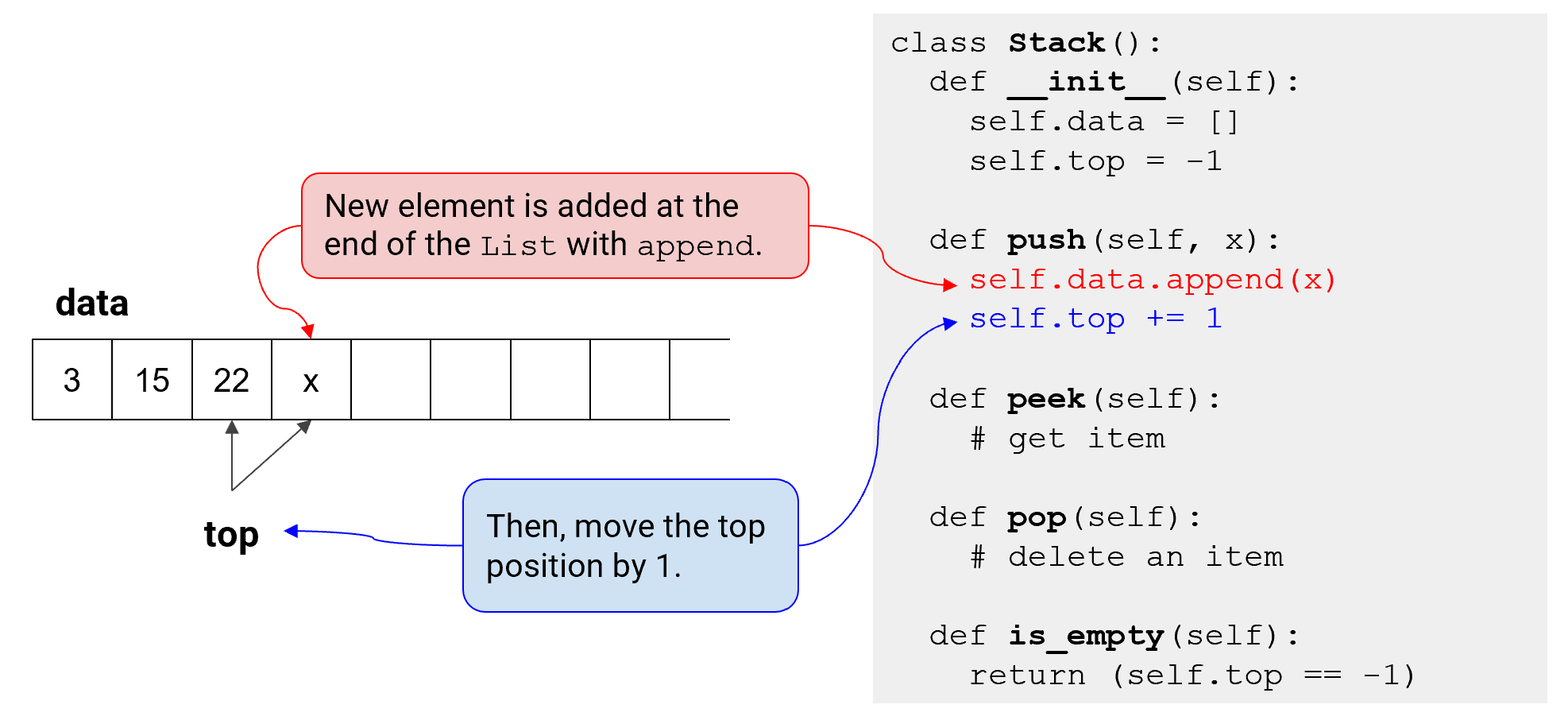
Push

삽입 위치를 특정하지 x (not specify)
새 요소는 오직 스택의 맨 뒤!!에 추가
리스트의 마지막에 append를 사용하여 새 요소 추가 & top(스택의 가장 최근 항목의 위치)을 1만큼 이동시킴

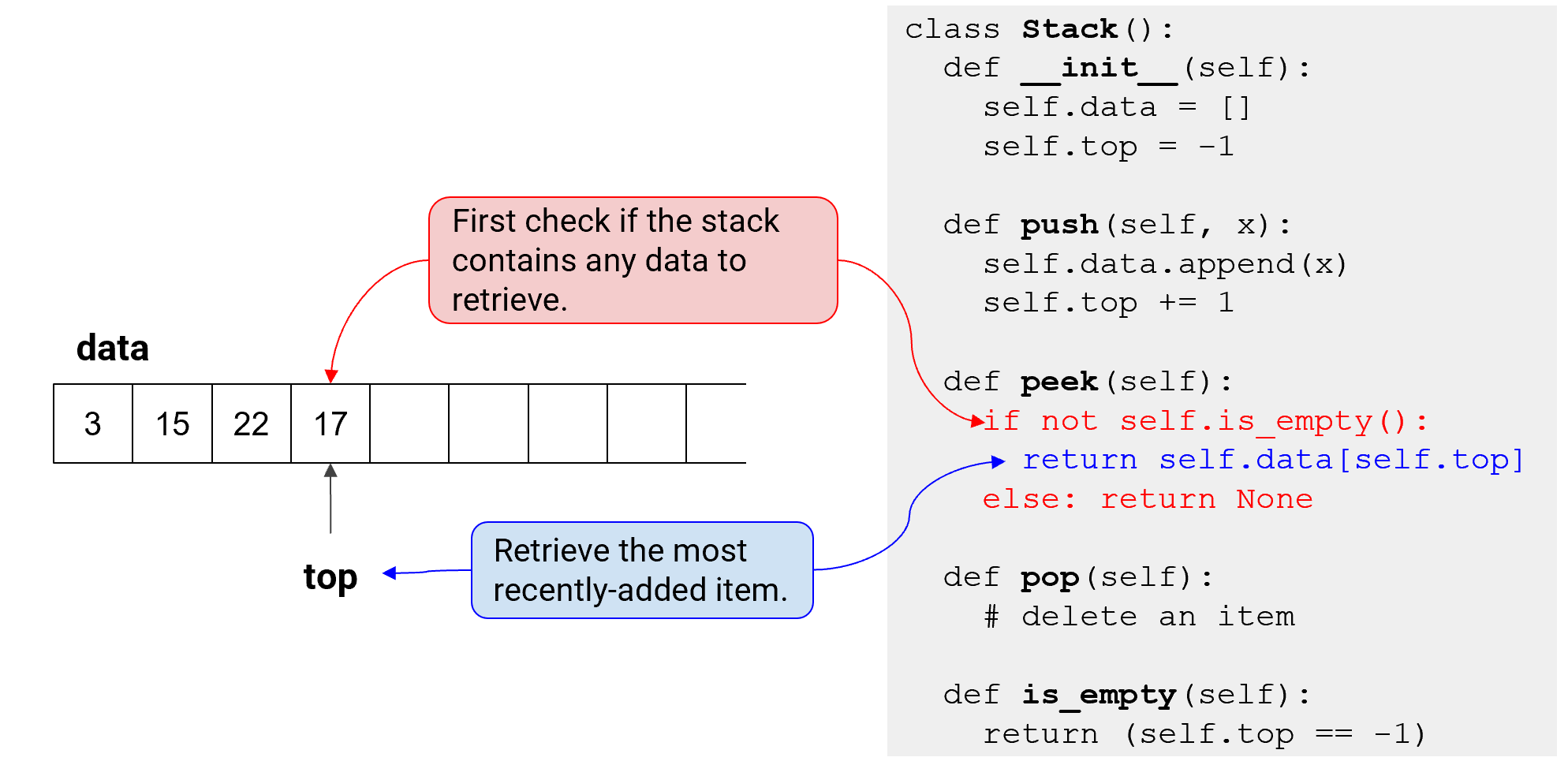
Peek

가져올(retrieve) 위치를 지정하지 x
항상 맨 뒤!!(최근저장)의 항목만 가져옴
1) 스택에 가져올 데이터가 있는지 확인 -> 2) 항목 가져옴

Pop

삭제할 위치를 특정하지 x
항상 맨 뒤!!(최근저장) 요소만 제거
맨 뒤의 요소를 제거한 후, top(최근저장 가르키는 index)를 -1만큼 이동시킴
python list를 사용할 경우 len(self.first)를 통해 top을 확인할 수 있음!

Reference-based Implementation(참조 기반 구현)

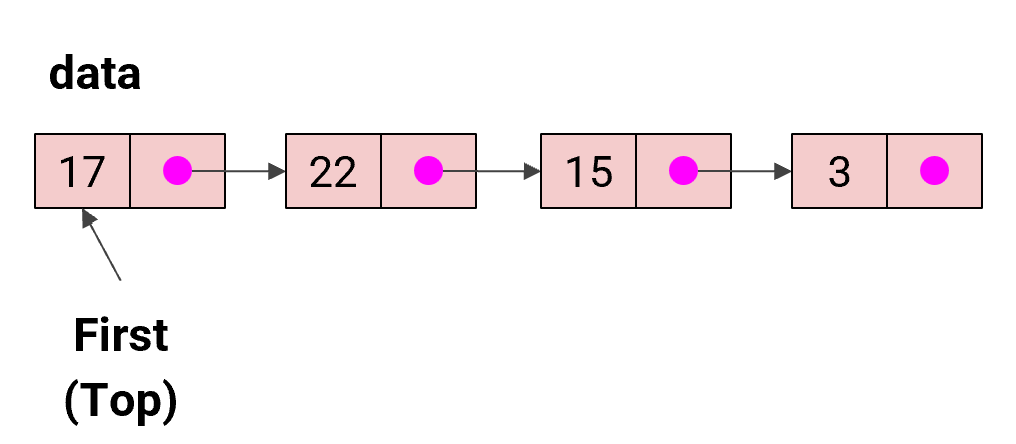
연결리스트(LinkedList)를 사용하여 구현 가능!
- 단일 연결 리스트(single LinkedList)는 첫 번째 요소부터 순차적으로 접근함
  - 따라서, 첫 번째 요소를 자연스럽게 스택의 top으로 이용하면 됨 (top index 지정할 이유 x)
push, peek, pop은 연결리스트 함수를 이용하여 구현하면 됨
- self.data.insert, get, delete로!!

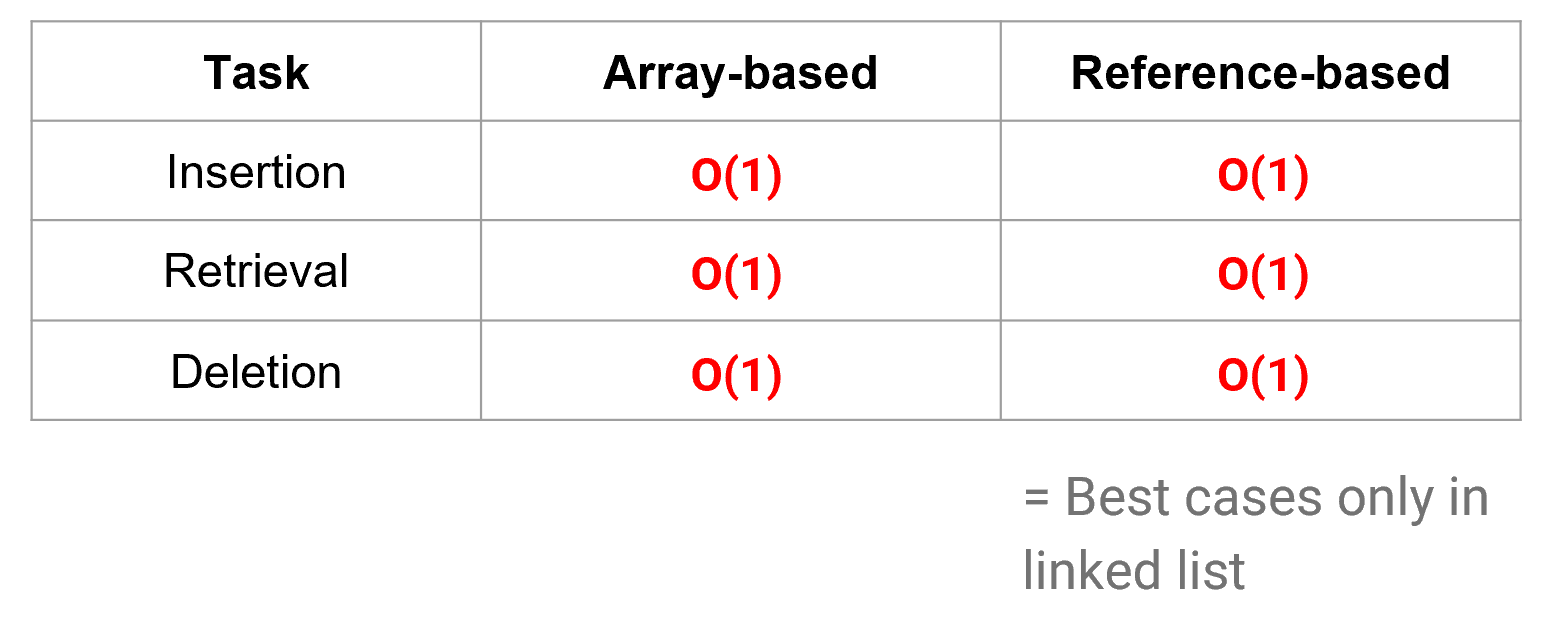
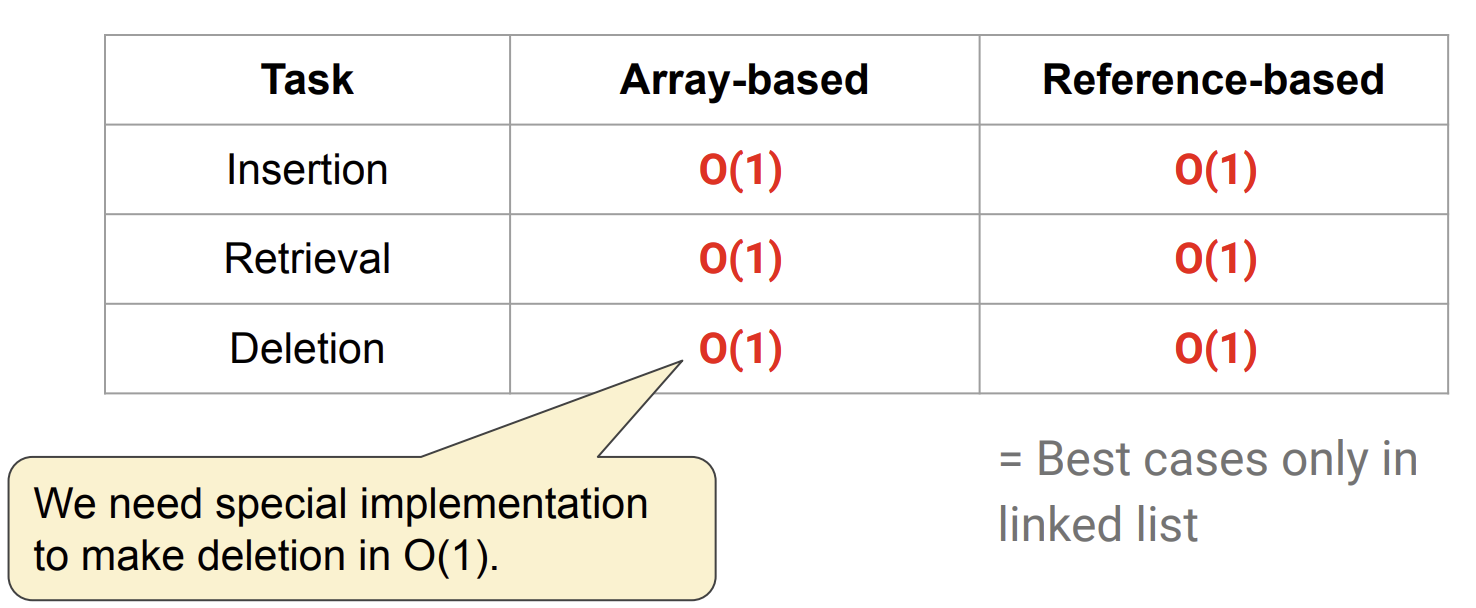
Stack's Time Complexity

-data와 문제가 특정 조건을 만족하면 배열이나 연결리스트보다 스택이 효율적일 때 있음!

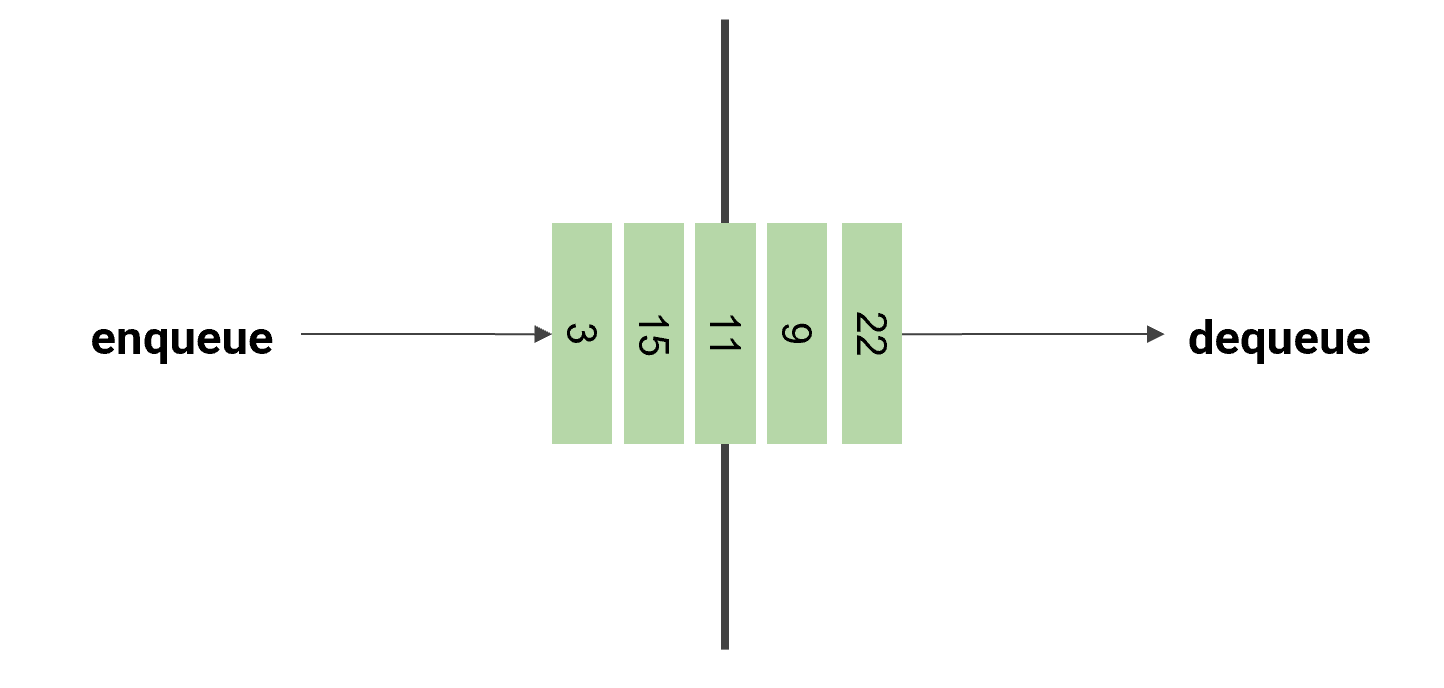
Queus(큐)

FIFO: First In, First Out => 먼저 들어간 것이 먼저 나옴
가장 먼저 추가된 항목에만 접근 가능 (가장 옛날에만 접근)

Queue Terminologies(용어)

새 항목 추가 => enqueue
가장 처음(==오래된) 항목 가져오기 => peek
항목 삭제 => dequeue

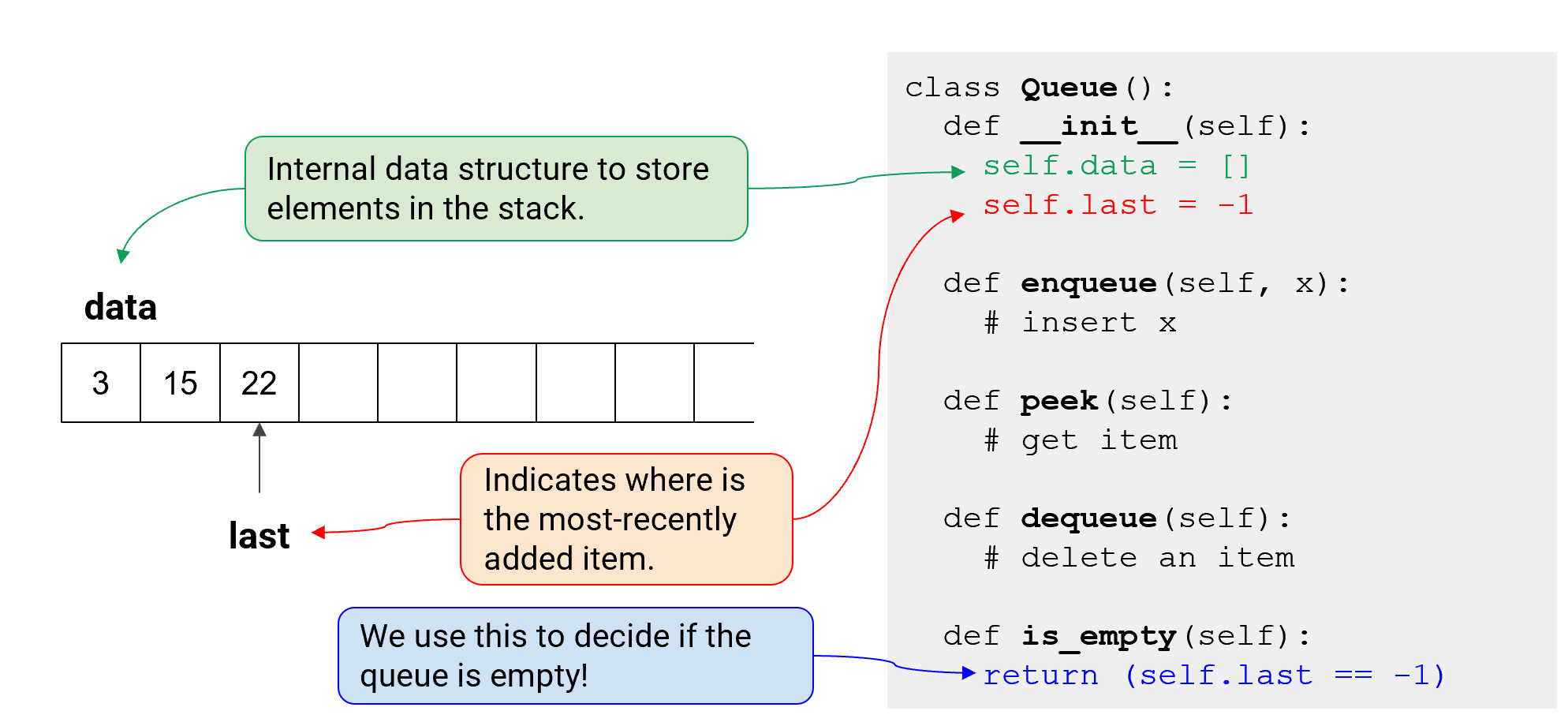
Queue Class Design

Array(배열)을 기반으로 stack을 구현함 => python list

queue에 항목을 저장하기 위한 내부 데이터 구조

last: 가장 최근에 추가된 항목의 위치를 나타냄
return (self.last == -1) top의 index가 -1로 지정됨으로써 큐가 비어있는지 판단하게 됨

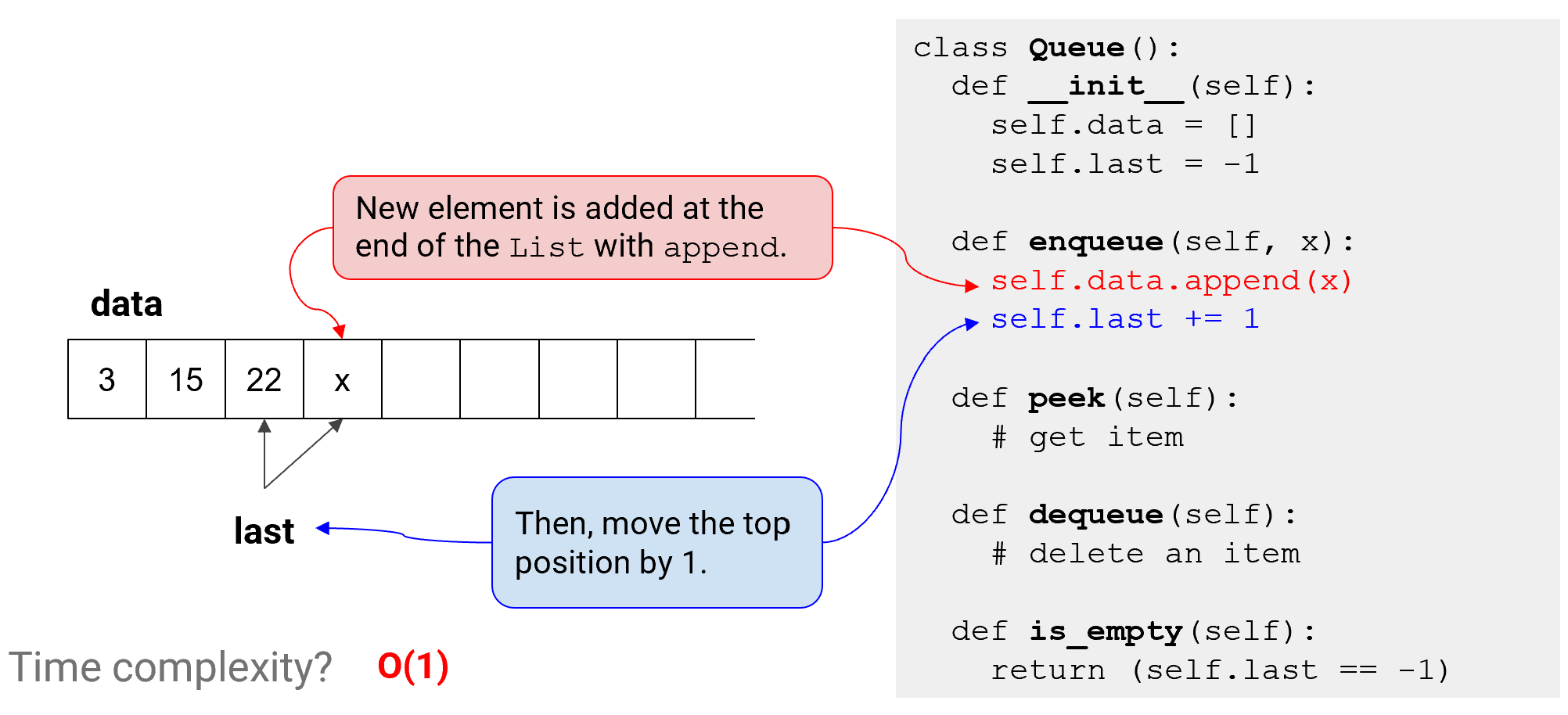
Enqueue

항상 마지막에 삽입!
stack의 push와 기능 동일함(삽입 위치만 다름) & last 위치만 1만큼 이동시킴

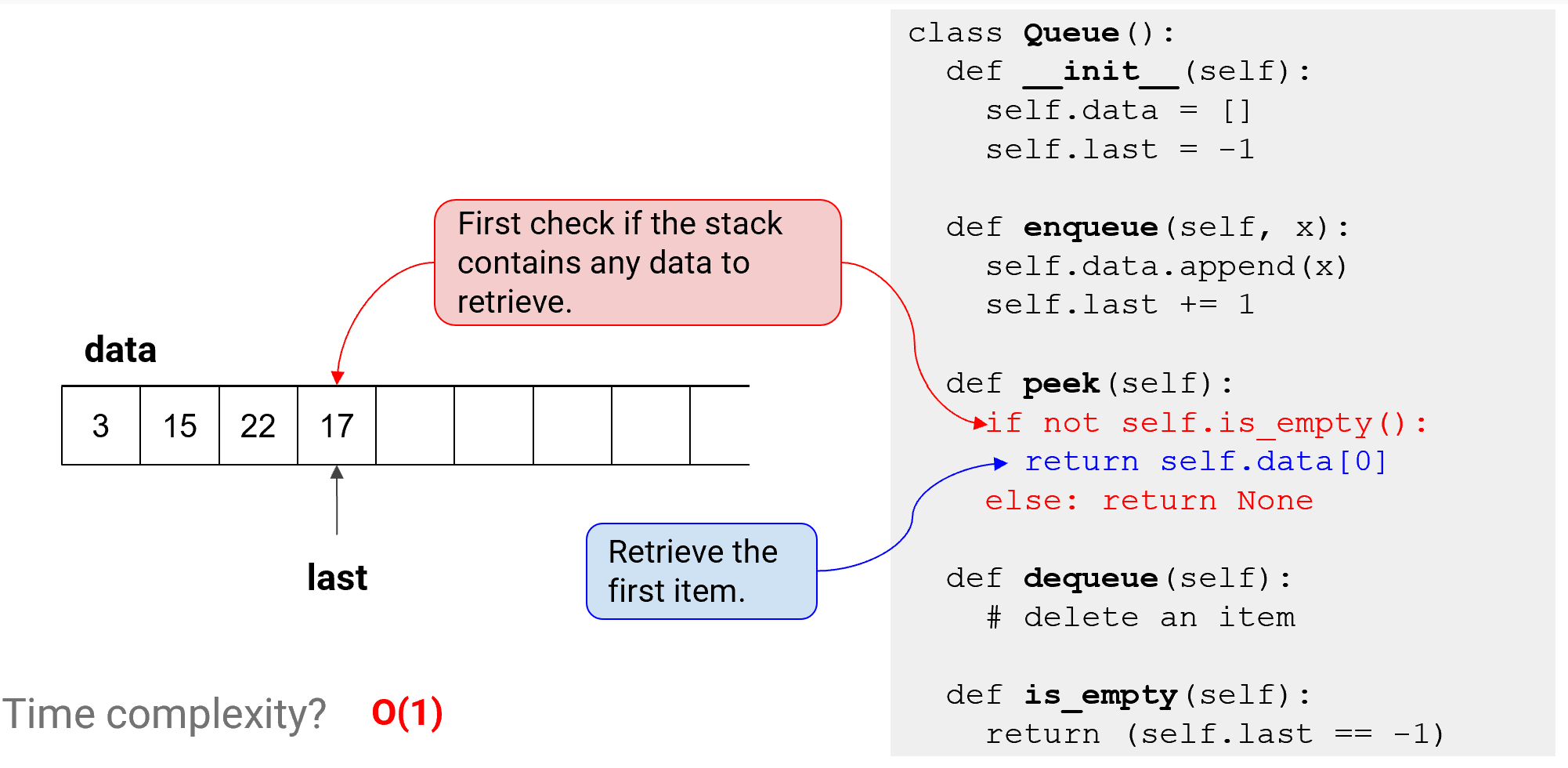
Peek

항상 가장 오래된(==첫번째 위치) 항목을 가져옴!
1) 큐에 가져올 데이터가 있는지 확인 -> 2) 항목 가져옴

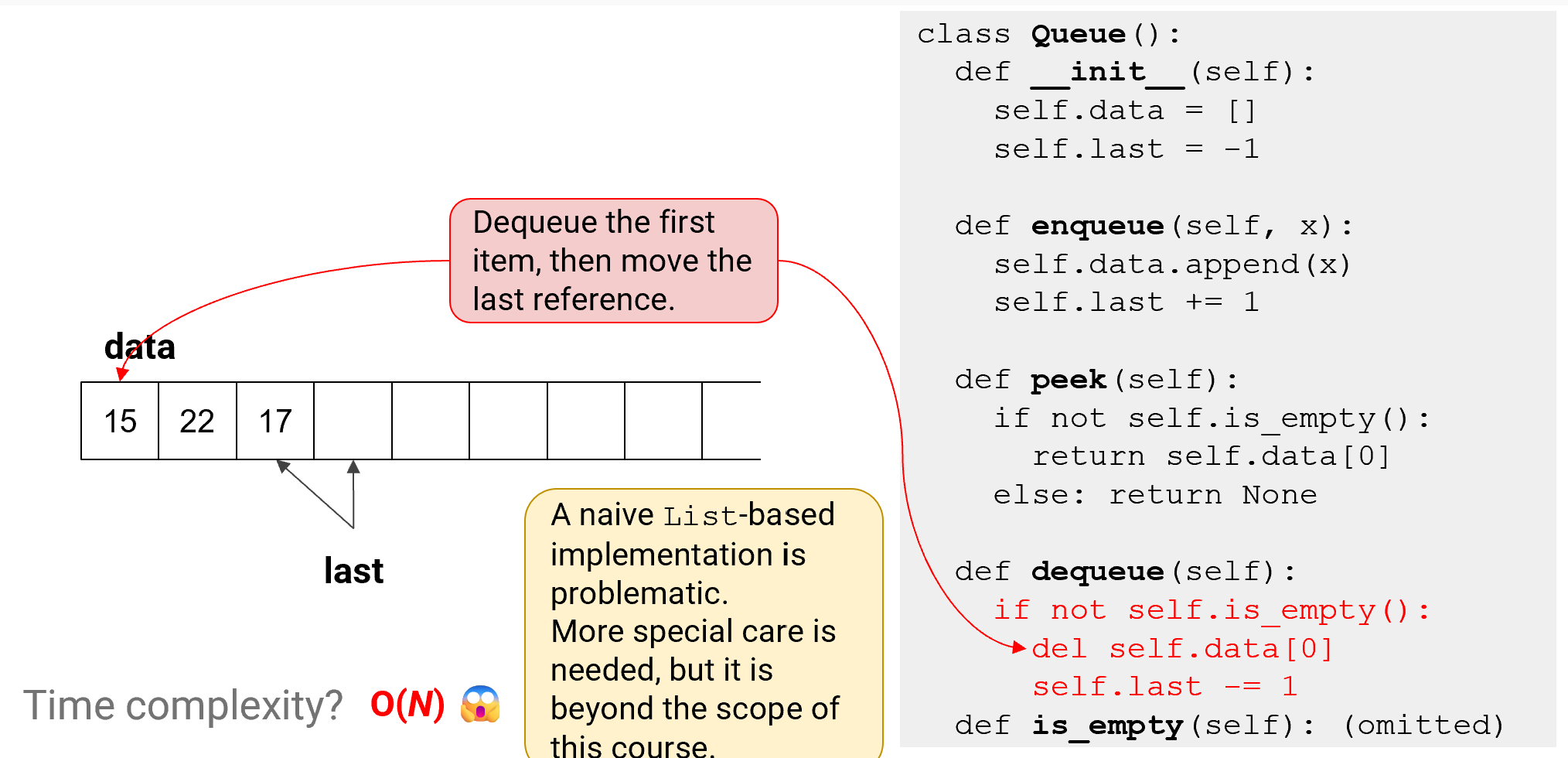
Dequeue

항상 가장 오래된(==첫번째 위치)를 삭제!
첫 번째 항목을 제거 후, last를 -1만큼 이동시킴
=> 기본적인 list 기반 구현에는 문제가 존재함.. 따라서 더 특별한 처리가 필요하다 (지금은 시간복잡도 O(N) 😱)

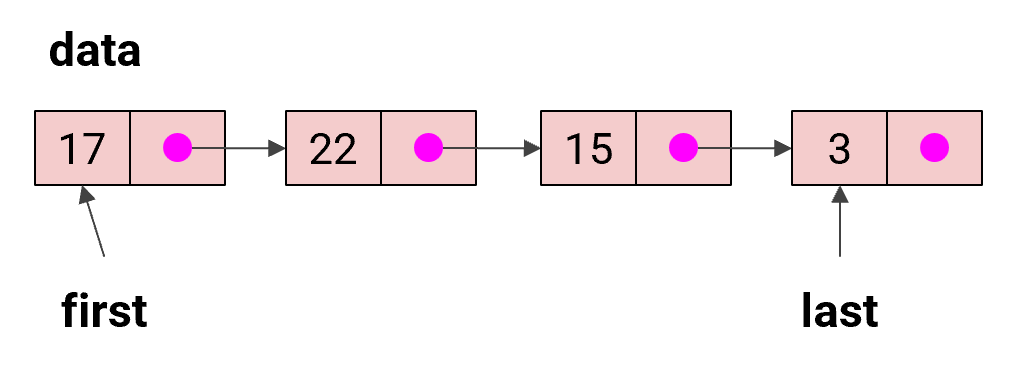
Reference-based Implementation(참조 기반 구현)

스택과 마찬가지로 LinkedList로 구현!
enqueue(추가), dequeue(삭제) -> 서로 다른 끝에서 수행하므로, 두 위치에 대한 참조를 유지할 수 있음
LinkedList는 기본적으로 시작 위치(self.first)를 제공하므로, 우리는 last 참조를 추가하면 됨
enqueue, peek, dequeue는 연결리스트 함수를 이용하여 구현하면 됨
- peek, dequeue
  - self.data.insert, get, delete로!!
- enqueue
  - 복잡하다.. -> 이유: last index를 알 수 x기 때문 (last index를 유지하더라도 항목을 삽입할 때 전체 리스트를 traverse해야하므로 O(N) 시간복잡도를 갖음)
  - 따라서, self.last 참조를 직접 활용!