Tree

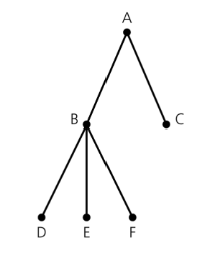
• 일반 트리 T는 분리된 하위 집합(disjoint subsets)으로 계속 분리됨
  • root: 단일 노드 r
  • subtrees of r: 일반 트리 집합
• 용어
  • node (vertex)
  • edge
  • parent
  • child
  • siblings
  • root
  • leaf
  • ancestor 조상
  • descendant 후손
  • subtree

Binary Tree

Definition

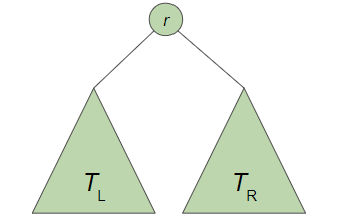
• T가 이진트리인 경우
  • T가 비어있는 경우
  • T가 3개의 분리된 하위 집합(disjoint subset)으로 분할된 경우
    • root: 단일 노드 r
      • left and right subtrees of r: 이진트리에서 나오는 최대 두 세트

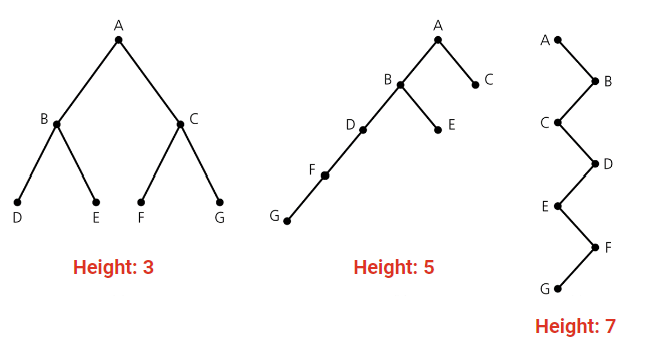
• Tree의 Height(높이)
  • root에서 leaf로 가는 가장 긴 node의 수

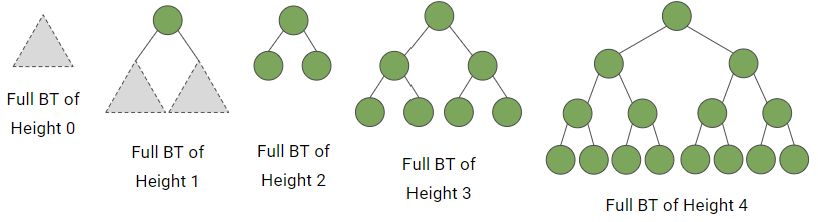
• Full Binary Tree
  • 트리가 비어있는 경우
  • 트리의 높이가 h일때, 왼쪽과 오른쪽 서브트리의 높이가 모두 h-1로 꽉 차있는 경우
    => 즉, 가능한 모든 위치에 노드가 꽉 차있는 트리를 말함!

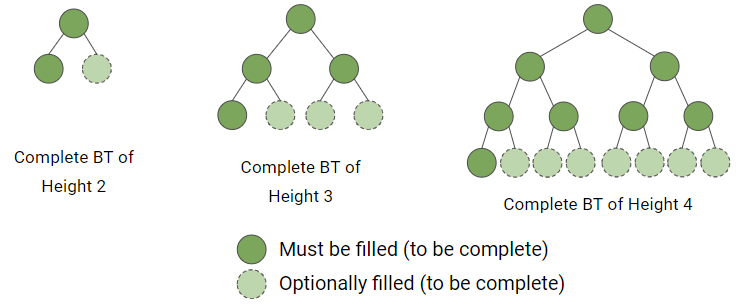
• Complete Binary Tree
  • 마지막 leaf 위까지는 다 차있고, 그 밑에는 다 안차있어도 됨

Array-based Implementation

• Recall: Array => 메모리 공간의 연속적인 고정 길이 칸(contiguous fixed-length chunk)을 가진 기본 데이터 구조
  • 배열로 List 구현하기 -> index를 mapping하는 것 간단했음
  • Q. binary tree에 지정된(designated) index를 할당하려면 어떻게 할까?
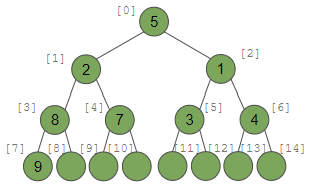
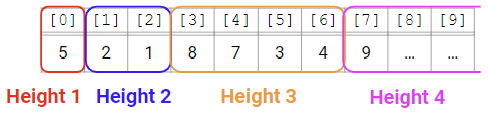
• tree가 가득찼다고 가정하고, 루트부터 왼 -> 오 순서로 인덱스를 할당함!
  • 트리가 거의 가득 차거나 완료된 경우에 가장 효율적!
• Q. node와 바로 연결된 자식(directed children)은 어떻게 파악할까?
  • tree를 사용하면, 일반적으로 root부터 leaf까지 순서대로 data에 접근함
  • tree를 사용하면, 일반적으로 root부터 leaf까지 순서대로 data에 접근함

Q. node와 child node를 연결하는 일반적 규칙은?

공식
1. Left child 찾기: [parent index] 2 + 1
2. Right child 찾기: [parent index] 2 + 2
<parent 찾기> [child index - 1] // 2

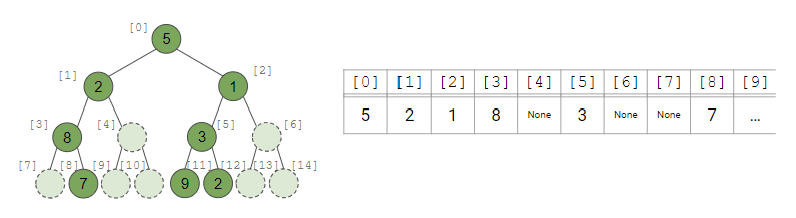
general case: node가 거의 안차있는 경우

• node가 비어있는 경우, None을 설정하거나 비어있음(emptiness)에 대한 다른 지표를 설정할 수 있음
• 트리가 full과 멀거나 완전하지 않은 경우(not complete) 이 구현은 효율성이 떨어짐

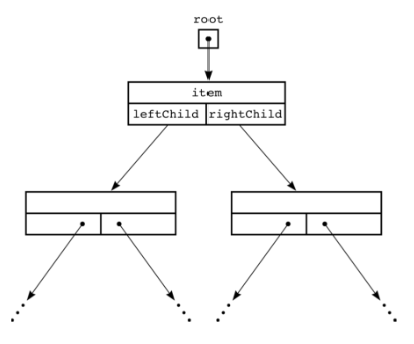
Reference-based Implementation

Parameter	First Image	Second Image
Dataset

• LinkedList와 비슷
  • 다른 node에 대한 단일 link를 갖는 것 ❌
  • 다른 node에 대한 두 개의 참조!⭕

Tree Traversal

• Traversal: tree의 모든 node를 돌면서 어떤 작업을 하고 싶을 때
  • 배열이나 linkedList와 다르게 tree는 모든 node를 visit하는게 복잡함!!

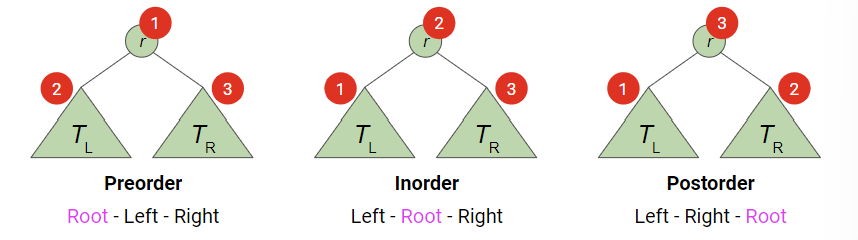
• 3가지 방법
  • 1. Preorder (Root-Left-Right)
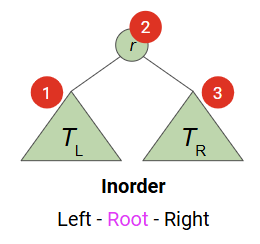
  • 2. Inorder (Left-Root-Right)
  • 3. Postorder (Left-Right-Root)
       => 각각의 subtree에서, 같은 rule이 재귀적으로 적용됨

예시

Tree Traversal Implementation

• 재귀(recursion)을 사용!
  • Base case: 빈 나무 => Do nothing!
  • General case: 재귀적 호출 2번 + 루트 visit
  • 순서는 Tree Traversal의 3가지 방법에 따라 달라짐 {Preorder, Inorder, Postorder}

Binary Search Tree

Definition

• 각 node에는 serach key가 있음
  • 이진 검색 트리의 search key는 중복되는 항목 x
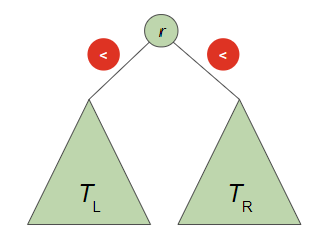
• 각 노드 n이 만족하는 것
  • 1. n's Key: 왼쪽 하위 트리(Tl)의 모든 key보다 큼
  • 2. n's Key: 오른쪽 하위 트리(Tr)의 모든 key보다 작음

Tree Operation

1. (insert) 이진 검색 트리에 새 항목을 삽입!
2. (Retrieve== search) 이진 검색 트리에서 지정된 search key로 항목을 검색!
3. (delete) 이진 검색 트리에서 지정된 search key가 있는 항목을 삭제!

=> 모든 level에서 {left subtree} < {root} < {right subtree}의 규칙을 따를 것!

1. Search(Retrieval)

<모든 tree를 다 traverse하지 않더라도 key를 빨리 찾을 수 있는 방법🍀>

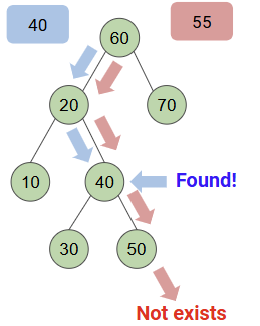
• Search : 주어진 key를 가진 node가 있는지 검색하고, 있는 경우 항목을 출력함
  • Main Idea: 각 node에서 추가로 검색할 subtree를 결정함 -> 3가지 경우!
    • [Case 1] If search key = 항목인 경우, 항목 찾은 것!
    • [Case 2] If search key < 항목인 경우, 항목이 왼쪽 subtree에 있는 것!
    • [Case 3] If search key > 항목인 경우, 항목이 오른쪽 subtree에 있는 것!

=> case2, case3의 경우 해당 subtree로 이동한 후 반복
leaf에 닿을 때까지 반복하되, 그때까지 case1을 충족하지 못하면 key가 tree에 없다는 결론을 내림

Implementation(구현)

• 재귀적 호출(recursive calls)을 이용한 구현

  

Time Complexity

• 각 node에서 두 값을 비교하고 어디로 갈지(left or right) 결정함 -> O(1)
  • root에서 leaf 까지의 길이만큼 => 따라서 최악의 시간 성능 == 나무의 높이(height)!
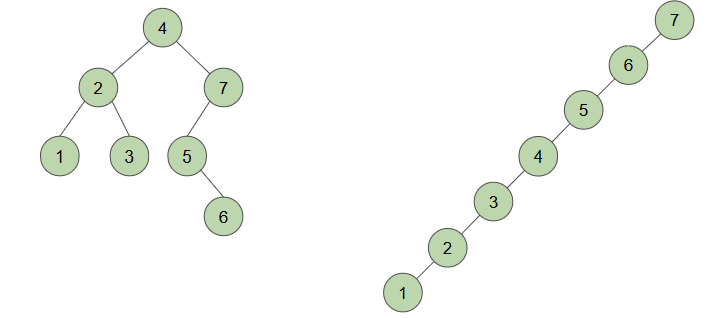
• Q. N(tree의 데이터 포인트 수) 측면에서 트리 검색의 점근적(asymptotic) 복잡성은(== Big O)?
  • [왼쪽 그림] 트리의 균형이 잡혀 있으면(complete O), 높이는 O(log N)에 가까워짐
  • [오른쪽 그림]트리의 균형이 맞지 않으면(Not complete), 높이는 O(N)에 가까워짐

2. Insertion

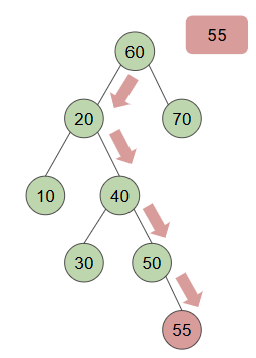
• Insertion: BST(이진탐색트리) 조건을 유지하면서 BST에 new key를 삽입함
  => 새 node를 배치할 적절한 위치를 찾아야함!
  • Main Idea: 삽입은 기본적으로 검색에 실패한 것으로, 항목이 존재하지 x면, 바로 그 자리에 새 node를 삽입하기!
    • [case1] If search key = 항목인 경우, 항목 찾은 것!
    • [Case 2] If search key < 항목인 경우, 항목이 왼쪽 subtree에 있는 것!
    • [Case 3] If search key > 항목인 경우, 항목이 오른쪽 subtree에 있는 것!

=> case2, case3의 경우 해당 subtree로 이동한 후 반복
leaf에 닿을 때까지 반복하되, 그때까지 case1을 충족하지 못하면 key가 tree에 없으므로 거기에 new node를 삽입!

Implementation(구현)

• 재귀적 호출(recursive calls)을 이용한 구현

  

3. Deletion

• Deletion: 주어진 key를 가진 node를 삭제하고 삭제 후 BST 조건을 유지
  => 중간 node를 삭제하면 tree가 끊어짐 😨
  • Main Idea:
    • [case1] 삭제할 node가 leaf인 경우, leaf를 그냥 제거!
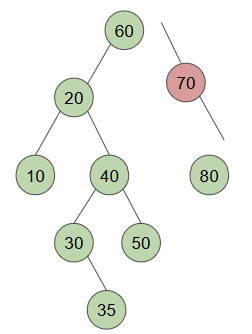
    • [case2] 삭제할 node가 single child만 가진 경우, subtree가 이어받음(take it over)
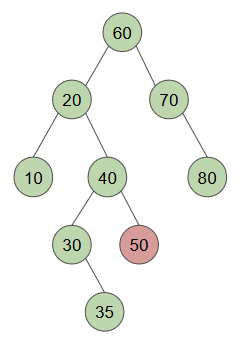
    • [case3] 삭제할 node에 child가 둘 다 있는 경우, 오른쪽 subtree에서 가장 왼쪽에 있는 leftmost 항목을 새 root로 선택!

case1

삭제 후 resulting tree가 여전히 연결되어 있으므로 간단히 제거!

case2

대상 노드에 자식이 하나 있으면, 기존의 자식이 부모 노드의 위치를 차지함
1. 70이 사라지면 resulting tree가 broken됨
2. 80이 70의 자리를 차지하면 더이상 broken X

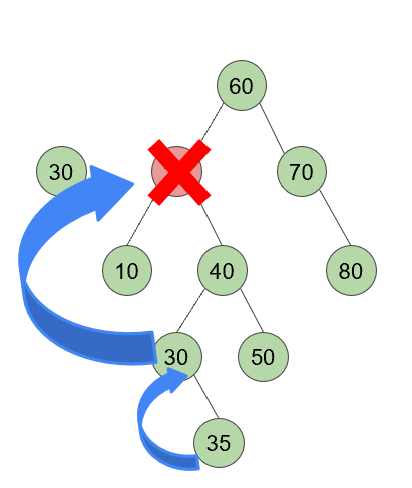
case3

• 대상 노드에 자식이 두 개(모두) 있으면, 대상의 오른쪽 subtree의 가장 왼쪽 node(== target의 immediate successor)를 새 root로 선택!
• 삭제 후 resulting tree는 broken
• 하위 트리가 두 개이므로 하위 트리 하나를 새 루트로 사용할 수 없음
• 결과 트리가 BST 조건을 만족하도록 하기 위해 삭제된 노드의 즉각적인 후속 트리를 선택, But resulting tree는 여전히 broken
  • Q. Why immediate successor? A. BST 조건을 충족
  • 삭제된 immediate successor node는 있는 경우 orphan right child를 입양해야됨
  • 여기서 left child가 존재하지 x것이 보장됨
• 마찬가지로, 대상의 왼쪽 subtree의 가장 오른쪽 node(== target의 immediate successor)를 새 root로 선택할 수도 있음

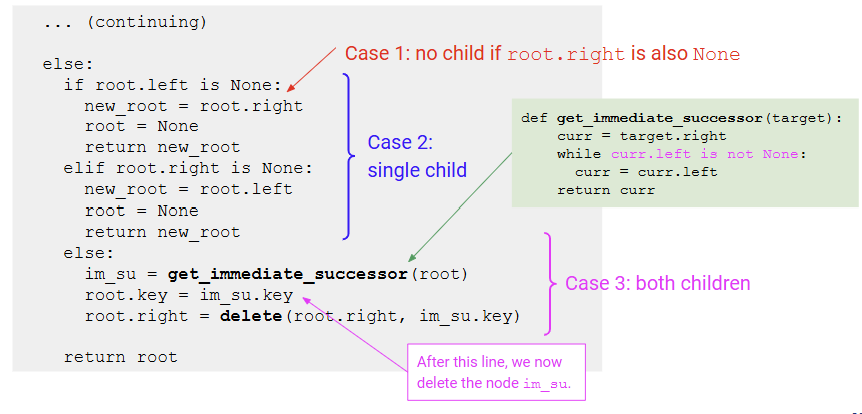
Implementation(구현)

delete함수는 삭제할 대상 node를 대체할 subtree를 반환함
자식이 둘다 없거나 하나만 있을경우
1. 지우는 대상의 left 자식 x: 오른쪽 자식이 삭제된 노드를 대체
2. 지우는 대상의 right 자식 x: 왼쪽 자식이 삭제된 노드를 대체
trick: im_su의 값만 root 값으로 덮어놓음(구조가 깨지면 너무 복잡해지기 때문!)
나중에 부른 delete는 boss children을 볼 경우가 없음
get_immediate_successor => 계속 왼쪽으로 가서 node 찾기

Revisiting the shape of BST

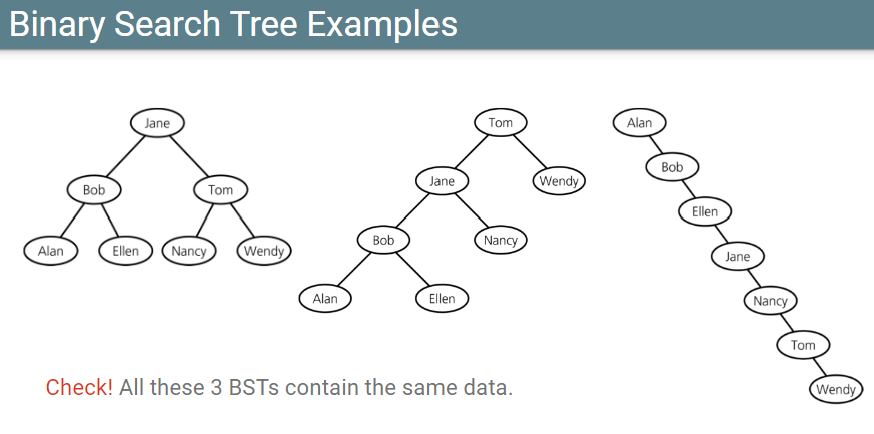
• Q. "4, 7, 2, 3, 5, 1, 6"을 삽입하면 BT의 모양은 어떻게 결정되나?
  • 동일한 데이터가 다른 순서로 주어졌다고 가정: "7, 6, 5, 4, 3, 2, 1"
  • 나무의 모양은 삽입 순서에 따라 결정됨!
  • But, datastream 자체를 제어할 수 없는 경우 多😥

Balanced Trees

< 일단 트리를 삽입하고 balance되게 만드는 법>

• 빠른 operation을 위해서는 tree의 균형을 맞추는 것이 좋음!
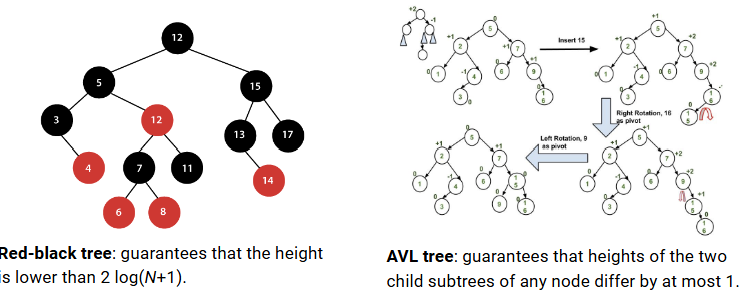
• 그림의 빨강-검정 트리: height가 2log(N+1)보다 낮도록 보장함 (full binary tree에 비해, 최대 높이 차이가 두 배까지만 나게)
• 그림의 AVL 트리: node의 두 subtree의 height가 최대 1까지 달라지도록 보장함 (full binary tree에 비해, 최대 높이 차이가 1차이만 나게)

Tree Sort

• 이진 검색 트리의 순서대로 탐색하면(Inorder traversal) => data가 정렬된 순서대로 나열됨
• BST 조건으로 인해, 모든 노드에서 left subtree의 모든 값 < root < right subtree의 모든 값 순서대로 visit!
  • 먼저, 모든 data를 BST에 삽입함 (insert) -> 각 요소 당 O(log N) x N개 = O(NlogN)
    (balanced tree를 사용한다고 가정)
  • 순서대로 횡단 (inorder traversal) -> O(N) (한 번에 하나의 node를 방문함)
• 따라서, 트리의 균형이 잡힌 경우 전체적으로 O(NlogN)
• 균형이 잡히지 않은 경우 최악의 성능 -> O(N2)

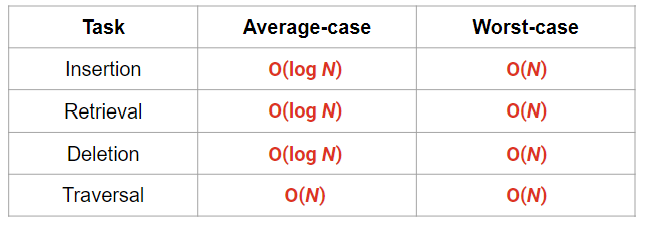
Binary Search Tree' Time Complexity

tree가 많이 unbalance일때를 가정하여, 시간 복잡도 구함!