시간 복잡도
"시간과 공간은 트레이드오프 관계이다"
(트레이드 오프: 하나가 증가하면 다른 하나는 감소한다, '반비례')
빠른 알고리즘 = 공간 사용량⬆️
많은 공간사용 = 실행 시간 ⬆️
느린 알고리즘 = 공간 사용량⬇️
적은 공간사용 = 실행 시간 ⬇️
📢 드물게 아닌 알고리즘도 존재하지만 대부분 트레이드오프 관계가 성립
- Input to Output이 될 때 까지 걸리는 시간
- 알고리즘을 구성한 명령어가 실행된 횟수 (Frequency of calling command)
- 어떤 알고리즘이 얼마나 걸리는지 여부 (cpu 사용량)
공간 복잡도 : 메모리를 얼마나 사용하는지에 대한 용량 개념
어떤 알고리즘이 메모리를 얼마나 사용하느가 (RAM 사용량)
공간과 시간 중 우선 순위는 요즘은 대게 시간이라고 한다
- 시간 복잡도를 고려하는 것은 최적화를 위해 필요하다
👉🏼데이터를 저장할 수 있는 메모리와 저장매체의 발전 덕에 과거보다 덜 필요하다
- Big-O(빅-오)
- Big-Ω(빅-오메가)
- Big-θ(빅-세타)
📢 빅오 표기법은 정확하게 쓰기에는 너무 길고 복잡한 함수를 "적당히 정확하게" 표현하는 방법이다
시간 복잡도의 빠른 순⏳
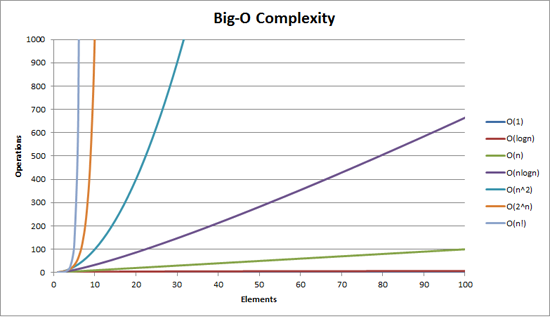
- O(log n) > O (n) > O(n log n) > O(n^2) > O(n^3) > O(2^n) > O(n!)
O(1) : 입력 자료의 수에 관계없이 일정한 실행 시간을 갖는다
O(log n): 입력 자료의 수에 따라 시간이 흐를수록 시간이 조금씩 증가 -> 로그는 매우 큰 입력값에서도 크게 영향을 받진 않는 편
👉 큰 문제를 일정한 크기를 갖는 작은 문제로 쪼갤 때 나타난다
👉🏼 이진 탐색 같은 효율이 좋은 검색 알고리즘
O(n): 입력 자료의 수에 따라 선형적인 실행 시간이 걸리는 경우 -> 알고리즘을 수행하는데 걸리는 시간은 입력값에 비례하며, 이러한 알고리즘을 선형 시간 알고리즘이라 부른다.
정렬되지 않은 리스트에서 최대 또는 최소값을 찾는 경우에 해당되며 모든 입력값을 적어도 한 번 이상 살펴봐야한다.
O(n log n): 큰 문제를 일정 크기를 갖는 문제로 쪼개고 (logn+logn+logn+...logn) 다시 그것을 모으는 경우
👉 효율 좋은 정렬 알고리즘
👉 quick sorting / heap sorting 등
O(n^2): 이중 루프 내에서 입력 자료를 처리할 때 -> 버블 정렬 같은 비효율적인 정렬 알고리즘이 해당 됨
👉 인접행렬을 이용한 bfs/dfs 알고리즘
O(n^3): 삼중 루프 내에서 입력 자료를 처리할 때
O(2^n): 피보나치의 수를 재귀로 계산하는 알고리즘이 해당된다.
n^2와 혼동될 수 있는데 2^n이 훨씬 크다
O(n!): 가장 느린 알고리즘으로 입력값이 조금만 커져도 계산이 어렵다
