문제

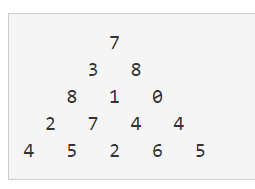
위 그림은 크기가 5인 정수 삼각형의 한 모습이다.

맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다.

삼각형의 크기는 1 이상 500 이하이다. 삼각형을 이루고 있는 각 수는 모두 정수이며, 범위는 0 이상 9999 이하이다.

입력

첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.

출력

첫째 줄에 합이 최대가 되는 경로에 있는 수의 합을 출력한다.

풀이

특정 위치에 도달하기 위에서는 바로 위 와 왼쪽 위 2가지 위치에서 내려올 수 있다. 따라서 이 2가지 경우를 생각해서 해결하면 된다. 2가지 경우의 값이 제일 큰 것과 현재 위치의 값을 더해주면 되는 것이다.

즉, 해당 위치의 값을 2차원 배열로 나타낸 것이 d[i][j]라 했을 때, d[i][j] = d[i][j] + max(d[i-1][j](바로 위), d[i-1][j-1](왼쪽 위))라고 할 수 있다.

또한, 입력을 받을 때 별도의 2차원 배열을 만들지 않고 바로 dp테이블에 저장해서 값을 갱신해주는 형태로 진행할 수 있다.

소스

import java.util.*;

public class Main {
	public static int n;

	public static int[][] d = new int[500][500];

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		n = sc.nextInt();

		for (int i = 0; i < n; i++) {
			for (int j = 0; j <= i; j++) {
				d[i][j] = sc.nextInt();
			}
		}

		// 위에서 2번째 줄부터 시작
		for (int i = 1; i < n; i++) {
			for (int j = 0; j <= i; j++) {
				// 위에서 오는 것, 왼쪽 위에서 오는 것
				int up, leftUp;
				// 왼쪽 위에서 오는 경우
				if (j == 0) {
					leftUp = 0;
				} else {
					leftUp = d[i - 1][j - 1];
				}

				// 위에서 오는 경우
				if (j == i) {
					up = 0;
				} else {
					up = d[i - 1][j];
				}

				d[i][j] = d[i][j] + Math.max(up, leftUp);
			}
		}

		int ans = 0;
		for (int i = 0; i < n; i++) {
			ans = Math.max(ans, d[n - 1][i]);
		}

		System.out.println(ans);
	}

}